本文共 3783 字，大约阅读时间需要 12 分钟。

一、题目描述

在一个迷宫游戏里，有一些小怪物要去攻击主角，现在希望给这些小怪物加上聪明的AI，让他们可以自动绕过迷宫中的障碍物，寻找到主角所在。 二、解题思路 迷宫游戏里的场景通常都是由小方格组成。假设我们有一个7*5大小的迷宫，图中红色格子是终点，绿色格子是起点，蓝色格子是一堵墙。 AI角色从起点开始，每一步只能向上、下、左、右移动1格，且不能穿越墙壁，那么如何让AI角色用最少的步数达到终点？

首先要引入两个集合和1个公式：

open_list：可到达的格子 close_list：已到达的格子 一个公式如下： F=G+H 每一个格子都具有F、G、H这三个属性： G：从起点走到当前格子的成本，也就是已经花费了多少步。 H：在不考虑障碍的情况下，从当前格子走到目标格子的距离，也就是离目标还有多远。 F：G和H的综合评估，也就是从起点到达当前格子，再从当前格子到达目标格子的总步数。

第一步：把起点放入open_list，也就是可到达格子的集合。

第二步：找出open_list中F值最小的方格作为当前方格。 第三步：找出当前方格上下左右所有可到达的格子，看他们是否在open_list或者close_list中，如果不在，则将他们加入open_list中。计算出相应G、H、F值，并把当前格子作为他们的父节点。 之后进行第二轮，我们需要一次又一次重复刚刚的第二不和第三步，直到直到终点为止。

三、代码实现

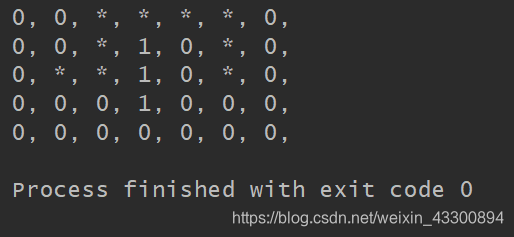
def a_star_search(start, end):    # 待访问的格子    open_list = []    # 已访问的格子    close_list = []    # 把起点加入open_list    open_list.append(start)    # 主循环，每一轮检查一个当前方格节点    while len(open_list) > 0:        # 在open_list中查找 F值最小的节点作为当前方格节点        current_grid = find_min_gird(open_list)        # 当前方格节点从openList中移除        open_list.remove(current_grid)        # 当前方格节点进入 closeList        close_list.append(current_grid)        # 找到所有邻近节点        neighbors = find_neighbors(current_grid, open_list, close_list)        for grid in neighbors:            if grid not in open_list:            # 邻近节点不在openList中，标记父亲、G、H、F，并放入openList                grid.init_grid(current_grid, end)                open_list.append(grid)        # 如果终点在openList中，直接返回终点格子        for grid in open_list:            if (grid.x == end.x) and (grid.y == end.y):                return grid    # openList用尽，仍然找不到终点，说明终点不可到达，返回空    return Nonedef find_min_gird(open_list=[]):    temp_grid = open_list[0]    for grid in open_list:        if grid.f < temp_grid.f:            temp_grid = grid    return temp_griddef find_neighbors(grid, open_list=[], close_list=[]):    grid_list = []    if is_valid_grid(grid.x, grid.y-1, open_list, close_list):        grid_list.append(Grid(grid.x, grid.y-1))    if is_valid_grid(grid.x, grid.y+1, open_list, close_list):        grid_list.append(Grid(grid.x, grid.y+1))    if is_valid_grid(grid.x-1, grid.y, open_list, close_list):        grid_list.append(Grid(grid.x-1, grid.y))    if is_valid_grid(grid.x+1, grid.y, open_list, close_list):        grid_list.append(Grid(grid.x+1, grid.y))    return grid_listdef is_valid_grid(x, y, open_list=[], close_list=[]):        # 是否超过边界        if x < 0 or x >= len(MAZE) or y < 0 or y >= len(MAZE[0]):            return False        # 是否有障碍物        if MAZE[x][y] == 1:            return False        # 是否已经在open_list中        if contain_grid(open_list, x, y):            return False        # 是否已经在closeList中        if contain_grid(close_list, x, y):            return False        return Truedef contain_grid(grids, x, y):    for grid in grids:        if (grid.x == x) and (grid.y == y):            return True    return Falseclass Grid:    def __init__(self, x, y):        self.x = x        self.y = y        self.f = 0        self.g = 0        self.h = 0        self.parent = None    def init_grid(self, parent, end):        self.parent = parent        if parent is not None:            self.g = parent.g + 1        else:            self.g=1        self.h = abs(self.x - end.x) + abs(self.y - end.y)        self.f = self.g + self.h# 迷宫地图MAZE = [    [0, 0, 0, 0, 0, 0, 0],    [0, 0, 0, 1, 0, 0, 0],    [0, 0, 0, 1, 0, 0, 0],    [0, 0, 0, 1, 0, 0, 0],    [0, 0, 0, 0, 0, 0, 0]]# 设置起点和终点start_grid = Grid(2, 1)end_grid = Grid(2, 5)# 搜索迷宫终点result_grid = a_star_search(start_grid, end_grid)# 回溯迷宫路径path = []while result_grid is not None:    path.append(Grid(result_grid.x, result_grid.y))    result_grid = result_grid.parent# 输出迷宫和路径，路径用星号表示for i in range(0, len(MAZE)):    for j in range(0, len(MAZE[0])):        if contain_grid(path, i, j):            print("*, ", end='')        else:            print(str(MAZE[i][j]) + ", ", end='')    print()