
数学建模(NO.18灰色预测)



 类比 O L S OLS OLS原理
类比 O L S OLS OLS原理 





 说实话,我是大部分都没看懂,以后看懂了来更新
说实话,我是大部分都没看懂,以后看懂了来更新  例子:
例子: 

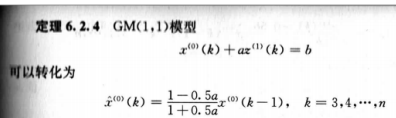


发布日期:2021-05-07 23:24:34
浏览次数:9
分类:精选文章
本文共 664 字,大约阅读时间需要 2 分钟。
灰色预测
一.灰色系统

二.GM(1,1)模型: Grey(Gray) Model
1.概述
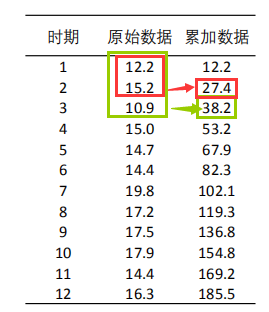
GM(1,1)是使用原始的离散非负数据列,通过一次累加生成削弱随机性的较有规律的新的离散数据列,然后通过建立微分方程模型,得到在离散点处的解经过累减生成的原始数据的近似估计值,从而预测原始数据的后续发展。
(我们在此课件中只探究GM(1,1)模型,第一个‘1’表示微分方程是一阶的,后面的‘1’表示只有一个变量)

2.原理介绍



 类比 O L S OLS OLS原理
类比 O L S OLS OLS原理 





 说实话,我是大部分都没看懂,以后看懂了来更新
说实话,我是大部分都没看懂,以后看懂了来更新 3.完全多重共线性问题再探究

4.准指数规律的检验
原则:
 例子:
例子: 
5.发展系数与预测情形的探究

6.GM(1,1)模型的评价

【1】残差检验


【2】级比偏差检验

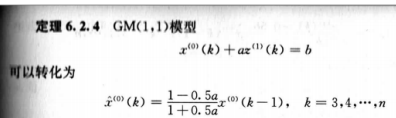

7.GM(1,1)模型的拓展


8.什么时候用灰色预测?
(1)数据是以年份度量的非负数据(如果是月份或者季度数据一定要用我们上一讲学过的时间序列模型);
(2)数据能经过准指数规律的检验(除了前两期外,后面至少90%的期数的光滑比要低于0.5); (3)数据的期数较短且和其他数据之间的关联性不强(小于等于10,也不能太短了,比如只有3期数据),要是数据期数较长,一般用传统的时间序列模型比较合适。发表评论
最新留言
初次前来,多多关照!
[***.217.46.12]2025年04月09日 07时39分28秒
关于作者

喝酒易醉,品茶养心,人生如梦,品茶悟道,何以解忧?唯有杜康!
-- 愿君每日到此一游!
推荐文章
uni-app请求头中携带token
2021-05-07
常用的 Git 命令和小技巧(1)
2021-05-07
vue中接收后台的图片验证码并显示
2021-05-07
springboot入门(1)---整合MyBatis
2021-05-07
Vue入门学习笔记(1)
2021-05-07
ECharts——双向柱状图
2021-05-07
Vue——引进bootstrap
2021-05-07
Vue——引进ivew
2021-05-07
趣谈win10常用快捷键
2021-05-07
数学建模(NO.18灰色预测)
2021-05-07
数学建模更新12(数学线性规划模型1)
2021-05-07
Android,SharedPreferences的使用
2021-05-07
VLAN与Trunk的原理及配置
2021-05-07
华为hybrid vlan配置
2021-05-07
OSPF路由重分发配置实例
2021-05-07
VS中使用c++函数显示找不到标识符
2021-05-07
JPEG压缩技术
2021-05-07
开发基于MFC的ActiveX控件的时候的一些消息处理
2021-05-07