本文共 9412 字，大约阅读时间需要 31 分钟。

数据结构实验9_图的遍历

• （1）实验目的
  通过该实验，使学生掌握图的几种存储结构，理解图的深度优先和广度优先遍历算法的思想和实现办法，
• （2）实验内容
  实现教材算法7.2利用邻接矩阵构造无向图的算法，在此基础上进行深度优先遍历和广度优先遍历。
• （3）参考界面

• （4）验收/测试用例

• 创建所示无向图

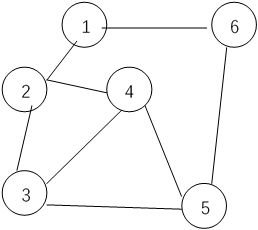
• 屏幕输出邻接矩阵
  0 1 0 0 0 1
  1 0 1 1 0 0
  0 1 0 1 1 0
  0 1 1 0 1 0
  0 0 1 1 0 1
  1 0 0 0 1 0

• 深度优先遍历
  屏幕输出： 1 2 3 4 5 6

• 广度优先遍历
  屏幕输出：1 2 6 3 4 5

一、设计思想

1. 无向图的存储结构采用 一维数组 存储顶点，二维矩阵存储 关联边，有关联的行、列交差矩阵元素值为1，反之为0.（可根据情况自行设置权值）

2. 对于图的构建，

   2.1 需要增加输入的异常情况做判断处理，提高程序的健壮性，对于顶点的个数需要大于0，对于弧的个数也需要限制 0-n*(n-1)/2.

   2.2 设置构建成功返回值status便于，下面操作的逻辑性

   2.3 关于 数值的输入（包括顶点和弧的信息），我采用的是 定义全局指针，开辟数组，初始化完成后，将指针指向目标数组，对于系列操作，只需传递指针参数即可

   2.4 需要注意的是，辅助数组的下标为 该 顶点值，当遍历的时候，可以直接visited[顶点]来 进行 输出逻辑判断

   2.5 数组、矩阵的下标都是从0开始，需要注意区分 和 顶点 值之间的关系，这里写了 根据 顶点值 查找 在一维数组 中的下标，对于不按照顺序输入 顶点弧 的信息也支持

3. 对于图的遍历

• 3.1 深度优先遍历DFS:，可以采用递归，也可以用 队列 + 循环 来实现

  • 3.1.1 递归实现
    对于非连通图的处理时候，需要注意 无限循环的bug
    核心思想就是，利用辅助数组，每次找 该顶点 所在 行的 最近的邻接点，然后递归下去，直到最后全部访问结束。关键是找的方法，利用辅助数组，实现不止是 最近的邻接点，而且要求是未访问过得，关键就是过滤掉访问过得顶点

  • 3.1.2 非递归实现
    在写 广度 优先遍历的时候，出现bug调试的时候实现的，利用队列加 + 循环，主要思想就是：开始拿到顶点，需要先进队列，出队时候访问该节点的时候，需要内层套循环，将未访问过的一条链上的 一个顶点入队，然后和 上面递归类似，出队的时候，找最近的未被访问过得一个邻接点，接着入队，出队，访问…直到全部访问完毕

  • 3.1.3 上述非递归的DFS只要将关键查找邻接点 的语句 稍微修改，就
    变成了BFS,即将每次入队一个邻接点，改为入队当前行的所有未访问的邻接点，每次将某个顶点的 所有 邻接点 全部入队

• 3.2 广度优先遍历BFS
  队列 + 循环
  开始先将逻辑头结点入队，然后进行出队、访问
  然后，将该节点的所有 未访问 的邻接点 全部入队
  接着就是依次重复入队出队、访问，直到全部访问完毕

二、源代码

#include<iostream>#include<stdio.h>#include<stdlib.h>using namespace std;typedef int Status; //一、图的邻接矩阵存储表示// 1. 最大顶点个数 #define MAX_VERTEX_NUM 20typedef int VRType;typedef int VertexType;// 2. 二维矩阵 typedef struct ArcCell{   	VRType adj;//权值 	} AdjMatrix[MAX_VERTEX_NUM][MAX_VERTEX_NUM]; // 3. 一维数组，绑定邻接矩阵 typedef  struct{   	VertexType vexs[MAX_VERTEX_NUM];//顶点数组 	AdjMatrix arcs;//绑定邻接矩阵 	int vexnum;//总的顶点个数 	int arcnum;//总的弧数 }MyGraph; // 4. 辅助标志数组，用于遍历bool visited[MAX_VERTEX_NUM];// 二、自定义队列用于广度优先遍历typedef int QElemType; typedef struct QNode {   		QElemType data;	struct QNode *next;}*QueuePtr;//把两个指针封装在一个结构体内 //front、rear都是指向队列节点的结构体指针 typedef struct{   	QueuePtr front;	QueuePtr rear;	}LinkQueue;  // 二、函数声明// 1. 构建无向网图Status CreateUDN(MyGraph &g) ;// 1.1 在顶点数组中找顶点对应 二维矩阵的 位置 int LocateVex(MyGraph g,int v) ;// 2. 输出邻接矩阵void printAdjMatrix(MyGraph g) ;// 3.1 深度优先遍历,默认从 一维 数组第一个顶点开始 void DFSTraverse(MyGraph g);// 3.2递归 void DFS(MyGraph g,VertexType v) ;// 3.3 查找 当前行 该邻接点的  下一个邻接点 VertexType NextAdjVex(MyGraph g,VertexType v);// 4. 广度优先遍历,默认从 一维 数组第一个顶点开始 void BFS(MyGraph g); // 5. 打印函数void printVex(VertexType v) ;//队列函数声明 // 1. 初始化队列函数void InitQueue(LinkQueue &Q) ;// 2. 销毁队列void DestoryQueue(LinkQueue &Q); // 3. 清空队列void ClearQueue(LinkQueue &Q) ;// 4. 队列判空bool JudgeEmpty(LinkQueue Q); // 5. 求队列长度int GetLength(LinkQueue Q); // 6. 获取队头元素QElemType GetFront(LinkQueue Q);// 7. 插入一个元素（入队） void InsertElem(LinkQueue &Q,QElemType elem) ;// 8. 删除一个元素（出队） QElemType  DeleteElem(LinkQueue &Q) ; int main(){   		//声明图	MyGraph g;				 	bool flag = true;	while(flag){   		cout<<"☆欢迎使用图的邻接矩阵构造和遍历小程序~☆"<<endl;		cout<<"==Design By 软6-司超龙-1925050351==" <<endl<<endl;		cout<<" 1. 构建网图"<<endl; 		cout<<" 2. 输出邻接矩阵"<<endl; 		cout<<" 3. 深度优先遍历"<<endl; 		cout<<" 4. 广度优先遍历"<<endl; 		cout<<" 5. 退出"<<endl<<endl;		cout<<"请输入相关指令完成相关操作~" <<endl;				int status;		int which;		cin>>which;		switch(which){   			case 1:				system("cls");				status = CreateUDN(g);				if(status == -1){   					cout<<"顶点个数有误！请重新构建无向网图~"<<endl<<endl; 				}else if(status == -2){   					cout<<"弧个数有误！请重新构建无向网图~"<<endl<<endl; 				}else{   					cout<<"无向图构建完成！"<<endl<<endl;				}				break;			case 2:				system("cls");				//根据构建操作成功返回值 判断 是否能进行接下来的操作 				if(status == 1){   					printAdjMatrix(g);				}				else{   					cout<<"请先构建图在进行输出！" <<endl<<endl;				}								break;			case 3:				system("cls");				//根据构建操作成功返回值 判断 是否能进行接下来的操作 				if(status == 1){   					DFSTraverse(g);					cout<<endl<<endl; 				}				else{   					cout<<"请先构建图在进行深度遍历！" <<endl<<endl;				}								break;			case 4:				system("cls");				//根据构建操作成功返回值 判断 是否能进行接下来的操作 				if(status == 1){   					BFS(g);					cout<<endl<<endl; 				}				else{   					cout<<"请先构建图在进行广度遍历！" <<endl<<endl;				}				break;						case 5:				system("cls");				cout<<"程序已关闭！欢迎下次使用~~"<<endl<<endl;				flag = false;				break;			default:				system("cls");				cout<<"您输入的指令有误！请正确输入指令~~"<<endl<<endl;					} 	} } // 三、函数实现// 1. 构建无向网图Status CreateUDN(MyGraph &g){   		cout<<"请输入顶点个数："<<endl;	cin>>g.vexnum;	//顶点个数不合法 	if(g.vexnum <=0) {   		//cout<<"顶点个数有误！请重新构建无向网图~"<<endl<<endl; 		return -1;	}			cout<<"请输入弧的个数："<<endl;	cin>>g.arcnum;	//弧的个数不合法 	if(g.arcs < 0 || g.arcnum > g.vexnum *(g.vexnum - 1) /2) {   		//cout<<"弧个数有误！请重新构建无向网图~"<<endl<<endl; 		return -2;	}		cout<<"请输入各顶点编号：" <<endl;	//构造顶点数组 	for(int i = 0;i<g.vexnum;i++){   		cin>>g.vexs[i]; 	} 	//初始化邻接矩阵	for(int i = 0;i<g.vexnum;i++){   		for(int j = 0;j<g.vexnum;j++){   			g.arcs[i][j].adj = 0;		}	} 	//构造邻接矩阵	int v1,v2,w;	int indexV1,indexV2;	for(int k = 0;k<g.arcnum;k++){   		cout<<"请输入节点之间的信息（邻接点和权值）："<<endl;		cin>>v1>>v2>>w;				//找位置		indexV1 = LocateVex(g,v1) ;		indexV2 = LocateVex(g,v2) ;		//indexV1 = v1 - 1;		//indexV2 = v2 - 1;				g.arcs[indexV1][indexV2].adj = w;		//无向图邻接矩阵对称		g.arcs[indexV2][indexV1] = g.arcs[indexV1][indexV2];	} 	return 1;		} // 1.1 在顶点数组中找顶点对应 二维矩阵的 位置 int LocateVex(MyGraph g,int v) {   	for(int i = 0;i<g.vexnum;i++){   		if(v == g.vexs[i]){   			return i;		}	}	}// 2. 输出邻接矩阵void printAdjMatrix(MyGraph g){   	for(int i = 0;i<g.vexnum;i++){   		for(int j = 0;j<g.vexnum;j++){   			cout<<g.arcs[i][j].adj<<" ";		}		cout<<endl;	} } // 3.1 深度优先遍历,默认从 一维 数组第一个顶点开始 void DFSTraverse(MyGraph g){   		for(int j = 0;j<g.vexnum;j++){   		visited[g.vexs[j]] = false;	}	//防止存在非连通的情况 	for(int i = 0;i<g.vexnum;i++){   		if(!visited[g.vexs[i]]){   			DFS(g,g.vexs[i]);		}	}	}// 3.2递归 void DFS(MyGraph g,VertexType v){   	//访问 当前顶点 	printVex(v);	visited[v] = true;		//到二维矩阵中找当前顶点行 未被访问 的顶点 	int v_next = NextAdjVex(g,v);	while(v_next > 0 ){   		if(!visited[v_next]){   			DFS(g,v_next);		}		else{   			return;		}			}	}/**// 3.3 查找 当前二维矩阵 v顶点所在 行的 第一个邻接点  VertexType FirstAdjVex(MyGraph g,VertexType v){	int indexHang = LocateVex(g,v);	for(int i = 0;i<g.vexnum;i++){		if(g.arcs[indexHang][i].adj == 1 && !visited[ g.vexs[i]]){			return g.vexs[i];		}	}		} */ // 3.3 查找 当前行该邻接点的  下一个邻接点 VertexType NextAdjVex(MyGraph g,VertexType v){   	int indexHang = LocateVex(g,v);	for(int i = 0;i<g.vexnum;i++){   		if(g.arcs[indexHang][i].adj == 1 && !visited[ g.vexs[i]]){   			return g.vexs[i];		}	}	return 0;	} // 3.4 DFS一种非递归的遍历法，利用队列 + 循环 void DFSOtherWay(MyGraph g){   		//辅助标志数组初始化 	for(int j = 0;j<g.vexnum;j++){   		visited[g.vexs[j]] = false;	}		//声明队列	//队列节点	LinkQueue Q;	Q.front = NULL;	Q.rear = NULL; 		InitQueue(Q);	for(int i = 0;i<g.vexnum;i++){   		//未访问的顶点，先打印，然后入队 		if(!visited[g.vexs[i]]){   			visited[g.vexs[i]] = true;			printVex(g.vexs[i]);			//入队 			InsertElem(Q,g.vexs[i]); 			//队非空 			while(!JudgeEmpty(Q)) {   				//出队一个 				int u =	DeleteElem(Q);				//求出队的顶点的邻接点 				VertexType v_next = NextAdjVex(g,u); 				 				 //存在邻接点 				while(v_next > 0 ){   										//未被访问 					if(!visited[v_next]){   						//访问 						visited[v_next] = true;						printVex(v_next);						//该邻接点的 所有的邻接点入队 						InsertElem(Q,v_next);					}					//break;					v_next = NextAdjVex(g,v_next); 													}			}		}	}}// 4. 广度优先遍历,默认从 一维 数组第一个顶点开始 void BFS(MyGraph g){   		//辅助标志数组初始化 	for(int j = 0;j<g.vexnum;j++){   		visited[g.vexs[j]] = false;	}		//声明队列	//队列节点	LinkQueue Q;	Q.front = NULL;	Q.rear = NULL; 		InitQueue(Q);	for(int i = 0;i<g.vexnum;i++){   		//未访问的顶点，先打印，然后入队 		if(!visited[g.vexs[i]]){   			visited[g.vexs[i]] = true;			printVex(g.vexs[i]);			//入队 			InsertElem(Q,g.vexs[i]); 			//队非空 			while(!JudgeEmpty(Q)) {   				//出队一个 				int u =	DeleteElem(Q);				//求出队的顶点的邻接点 				VertexType v_next = NextAdjVex(g,u); 				 				 //存在邻接点 				while(v_next > 0 ){   										//未被访问 					if(!visited[v_next]){   						//访问 						visited[v_next] = true;						printVex(v_next);						//该邻接点的 所有的邻接点入队 						InsertElem(Q,v_next);					}					//break;					v_next = NextAdjVex(g,u); 													}			}		}	}} // 5. 打印函数void printVex(VertexType v) {   	cout<<v<<" ";}//自定义队列// 1. 初始化队列函数void InitQueue(LinkQueue &Q){   		Q.front = (QueuePtr )malloc(sizeof(QNode));	Q.rear = Q.front;			} // 2. 销毁队列void DestoryQueue(LinkQueue &Q){   	//队列元素为空 	if(Q.front == Q.rear){   		free(Q.front);		Q.front = NULL;		Q.rear = NULL;	}	//队列不为空，边移动，边释放空间，rear紧邻在front前开路 	else{   		while(Q.front){   			Q.rear = Q.front->next;			free(Q.front);			Q.front = Q.rear;		}		Q.front = NULL; 			}		} // 3. 清空队列void ClearQueue(LinkQueue &Q){   	InitQueue(Q);	}// 4. 队列判空bool JudgeEmpty(LinkQueue Q){   	if(Q.front == Q.rear){   		return true;	}	else{   		return false;	}} // 5. 求队列长度int GetLength(LinkQueue Q){   	int length = 0;	while(Q.front != Q.rear){   		length ++;		Q.front = Q.front->next;	}	return length;} // 6. 获取队头元素QElemType GetFront(LinkQueue Q){   		return Q.front->next->data;	}// 7. 插入一个元素（入队） void InsertElem(LinkQueue &Q,QElemType elem){   		QueuePtr p = (QueuePtr )malloc(sizeof(QNode));	p->data = elem;		Q.rear->next = p;	Q.rear = p;}// 8. 删除一个元素（出队） QElemType  DeleteElem(LinkQueue &Q){   		//注意顺序，Q.front指向的当前节点不做数据节点 	Q.front = Q.front->next;	QElemType elem = Q.front->data;		return elem; } // 9. 输出所有的元素QElemType PrintElem(QueuePtr p){   		return  p->data;} 

三、部分程序截图

四、错误bug截图

五、实验结果运用

1. 练习实现了 邻接矩阵无向图的 构建、两种DFS遍历方法、一种BFS遍历方法
2. 加深了对邻接矩阵、辅助标记数组等的理解
3. 出现了不少错误和bug,一步步的调试，分析最后解决完善程序
4. 最核心的就是 怎么 根据辅助 数组，在邻接矩阵 中找 当前目标顶点的 邻接点
   4.1． 递归一次找一个最近的未访问的邻接点—》DFS
   4.2. 非递归一次将当前顶点的 一个 最近未访问邻接点入队—》DFS
   4.3. 非递归一次将当前顶点的 全部 未访问的邻接点入队----》BFS