本文共 7804 字，大约阅读时间需要 26 分钟。

1背景介绍

1.1 工厂选址问题 工厂选址问题是运筹学中的经典问题之一，它描述的是在综合考虑工厂的建造成本、生产量，产品的运输成本，各地的需求量等因素后，如何制定适当的选址方案和物流运输方案来完成企业的生产经营活动。该问题的研究模型具有相当的普适应，其不仅仅在物流领域，还在生产生活，甚至军事中都有着非常广泛的应用。 1.2 模拟退火算法 模拟退火算法（Simulated Annealing，SA）来源于与固体退火的相似性，同时采用Metropolis准则（以概率接受新状态）做为接受准则。所谓的固体退火是一个获取固体低能晶格状态的热处理过程。首先将固体加热，使其融化为完全无序的液态，此时粒子处于自由运动的状态；然后逐渐降温，粒子运动逐渐趋于有序，当温度降低到结晶程度，粒子运动变为围绕晶格点的微小振动，液体凝固成固态晶体。1983年，Kirkpatrick充分利用了固体退火原理提出了模拟退火算法。算法的核心思想模拟了固体退火过程，在求解优化问题上表现出较强的稳健性、全局性和适用性。下面是退火算法的要素与固体退火过程的粗略对应。关于模拟退火算法的详细介绍请看

固体退火	退火算法
粒子的一个状态 i	优化状态的一个解 x
能量最低的一个状态	最优解
系统的能量	目标函数
温度	控制参数（决定接受新解的概率）
某一恒温状态下趋于热平衡	产生新解—判断（接受、舍弃）

2 问题描述

以离散工厂选址问题为例，假设有n个工厂为m个配送中心送货，每个配送中心的需求量为bj，j=1,2,…，m。在满足配送中心需求的前提下，可以选取任意工厂组合来生产运输产品。假设如果选定某个工厂，这需要固定成本di（可以理解为建筑成本或者运营成本），i=1,2,…n,且每个工厂的生产能力为ai。如果从工厂i到配送中心j的单位运输成本为cij，那么在满足配送中心的需求量的情况下，如何制定选址方案（选哪些工厂）和运输方案，才能使得总费用最小？

3 Python代码设计

3.1 参数设置 考虑由5个工厂（A-E）到10个配送中心（0-9）组成的工厂选址问题，参数设置如下： （1）各工厂的供应能力、各地需求量、建造/运营的固定费用：

supply_capacity = [4500, 3500, 5000, 3000, 2500]demand = [729, 630, 321, 293, 251, 573, 207, 732, 481, 783]fix_cost_lst = [304, 281, 459, 292, 241]

（2）运价表（保存在了一个名为‘transcost.csv’的文件中）

A   B   C   D   E0  9   2   3   7   31  5   1  10   6   52  6   4   5   3   63  8   6   7   3   44  8   7   5   6   85  1   7   1   5   46  9   1   8  10  107  8   5   5   3   78  4  10   8   5   89  3   5  10   7   3

（3）随机生成初始选址方案

location = np.random.randint(0,2,5)

3.2 程序代码

代码主要分为两大模块：一是根据选址方案计算最小总费用，二是使用退火算法对选址方案进行优化。 （1）首先导入需要的包，读取数据，设置初始参数。

import pandas as pd   import numpy as npimport pulpimport mathimport matplotlib.pyplot as pltdata = pd.read_csv(r'transcost.csv')demand = [729, 630, 321, 293, 251, 573, 207, 732, 481, 783]supply_capacity = [4500, 3500, 5000, 3000, 2500]fix_cost_lst = [304, 281, 459, 292, 241]dic = {   0:'A',1:'B',2:'C',3:'D',4:'E'}  #建立字典方便后面通过DataFrame组合相应的运价表

（2）迭代过程中选址方案的变化是一个部分随机的过程，这个过程中可能会产生需求量得不到满足的选址方案，这时就需要对不满足条件的方案进行调整：如果所有的需求量大于选中工厂的总供应量，那么随机添加一个未被选中的工厂，直到需求量能够得到满足。

#计算选址方案的总供应量def Cal_total_capacity(location,capacity):    total_capacity_lst = [capacity[i] for i in range(len(location)) if location[i] == 1]    return sum(total_capacity_lst)# 对不满足条件的选址方案进行修正def fixpop(location,capacity,demand):    while sum(demand) > Cal_total_capacity(location, capacity):        ind = np.random.randint(0,len(location))        if location[ind] == 0:            location[ind] = 1    return location

（3）根据选址方案组合产生相应的运价表。如选址方案为[1,0,1,1,0],则相应选取data的第[‘A’,‘C’,‘D’]列，组合为该方案下的运价表。

def Get_Translist(location,data,dic):    transcost = [list(data[dic[i]]) for i in range(len(location)) if location[i] == 1]    return transcost

（4）有了选址方案和对应的运价表，开始利用pulp计算最优的运输方案。函数是参考这里的代码（https://www.jianshu.com/p/9be417cbfebb），我把这部分理解为一个求解运输问题的包，可以不用搞懂代码逻辑，原代码稍作改变就可以直接拿来解运输问题。

def transportation_problem(costs, x_max, y_max):    row = len(costs)    col = len(costs[0])    prob = pulp.LpProblem('Transportation Problem', sense=pulp.LpMinimize)    var = [[pulp.LpVariable(f'x{i}{j}', lowBound=0, cat=pulp.LpInteger) for j in range(col)] for i in range(row)]    flatten = lambda x: [y for l in x for y in flatten(l)] if type(x) is list else [x]    prob += pulp.lpDot(flatten(var), costs.flatten())    for i in range(row):        prob += (pulp.lpSum(var[i]) <= x_max[i])    for j in range(col):        prob += (pulp.lpSum([var[i][j] for i in range(row)]) == y_max[j])    prob.solve()    return {   'objective':pulp.value(prob.objective), 'var': [[pulp.value(var[i][j]) for j in range(col)] for i in range(row)]}

（5）计算某一满足条件的选址方案下的最小费用（包括运输费用和固定费用）

def Cal_cost(location):    pop = fixpop(location,supply_capacity,demand)   #对原来的选址方案进行检验修正，返回处理过的选址方案 pop    fix_cost = 0    capacity_new = []    for i in range(len(pop)):        if pop[i] == 1:            fix_cost += fix_cost_lst[i]              #计算该方案下的固定费用fix_cost            capacity_new.append(supply_capacity[i])  #capacity_new是选址方案pop对应的供应能力列表    translist = Get_Translist(pop, data, dic)        #得到运价表    costs = np.array(translist)        max_plant = capacity_new    max_cultivation = demand    res = transportation_problem(costs, max_plant, max_cultivation)  #求解    return res['var'],res["objective"] + fix_cost    #返回的第一个值是pop的最优运输方案，第二个值是pop的最小总费用

Cal_cost(location) 函数是第一部分的最终目标，它可以输入选址方案（location），输出最小总费用。写到这里，第一大部分（根据选址方案计算总费用）代码完成。下面就开始为退火做准备。

（6）获取退火的初始温度。初始温度的获取目前没有统一的规则，这里参考其他博客里获取初始温度的方法，可以获取较合适的初始温度。np.random.permutation()函数用来随机打乱列表排序。

def GetInitialTem(location):    cost1 = 0 ; cost2 = 0 ; dif = 0    for i in range(10):        location1 = list(np.random.permutation(location))        location2 = list(np.random.permutation(location))        cost1 = Cal_cost(location1)[1]        cost2 = Cal_cost(location2)[1]        difNew = abs(cost1 - cost2)        if difNew >dif:            dif = difNew    pr = 0.5    T0 = dif / pr    return T0

（7）随机产生扰动，得到新解。扰动的方法是随机选择location中的一个值进行0-1互换，返回新的选址方案

def Disturbance(location_old):    location_new = location_old.copy()    ind = np.random.randint(0,len(location_new))    if location_new[ind] == 0:        location_new[ind] = 1    else:        location_new[ind] = 0     return location_new

（8）接受准则函数，用来判断是否接受新解，是整个算法的关键所在。函数的输入deltaE指新值（ValueNew）与旧值（ValueOld）之间的差，T是当前的温度。如果deltaE<0,则表示新解优于旧解，函数返回1，表示接受新解；如果deltaE>0（新解劣于旧解），则以（probility>随机数）的概率接受新解。初始时温度较高，probility较大，接受新解的概率较大，可以很好的跳出局部最优解，防止早熟；但当温度逐渐减小，退火过程逐渐趋于稳定，接受劣解的概率变小，结果会慢慢趋近优化问题的最优解。

def Judge(deltaE,T):    if deltaE < 0:        return 1    else:        probility = math.exp(-deltaE/T)        if probility > np.random.random():            return 1        else:            return 0

到这里，第二部分的退火过程也准备完。接下来就是设置代码的主函数部分。

location = np.random.randint(0,2,5)    #随机生成初始选址方案ValueOld = Cal_cost(location)[1]       #计算初始方案的最小费用count = 0							   #计数器record_value = []					   #空列表，用来储存每一个被接受的解tmp = GetInitialTem(location)		   #初始温度tmp_min = 1e-5						   #最小温度，和计数器一起用于判定退火过程的结束点alpha = 0.98						   #控制退火过程的快慢，即每产生一次较优解，温度下降（0.02*当前温度）

开始退火。

while (tmp > tmp_min and count < 2000):    location_n = Disturbance(location)     #根据旧的选址方案产生新的选址方案    location_new = fixpop(location_n, supply_capacity, demand)    #对新的选址方案进行检验和修正    ValueNew = Cal_cost(location_new)[1]   #计算新选址方案的最小总费用    deltaE = ValueNew - ValueOld           #比较新旧方案的费用    if Judge(deltaE, tmp) == 1:			   #如果接受新解        location = location_new			   #更新选址方案和最小总费用并记录	        #print(ValueNew)				   #可以用来监视程序执行过程中的结果。                                           #否则代码运行时间较长，我一直怀疑电脑卡住了。。。        ValueOld = ValueNew        record_value.append(ValueNew)    if deltaE < 0 :        tmp = tmp * alpha				   #如果生成了一个较优解，则退火，温度下降    else:        count += 1#打印结果print('='*80,'\n',      'The minvalue is: {}'.format(min(record_value)),'\n',      'The best location is: {}'.format(location),'\n',      'The best transport schedule is: {}'.format(Cal_cost(location)[0]),'\n',      '='*80)

退火过程的可视化

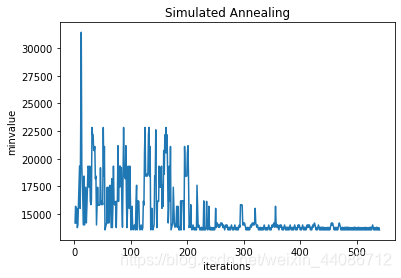
x = len(record_value)index = [i+1 for i in range(x)]plt.plot(index,record_value)plt.xlabel('iterations')plt.ylabel('minvalue')plt.title('Simulated Annealing')

4 运行结果：

================================================================================  The minvalue is: 13562.0  The best location is: [1 1 0 1 0]  The best transport schedule is:  [[0.0, 0.0, 0.0, 0.0, 0.0, 573.0, 0.0, 0.0, 481.0, 783.0],  [729.0, 630.0, 0.0, 0.0, 0.0, 0.0, 207.0, 0.0, 0.0, 0.0],   [0.0, 0.0, 321.0, 293.0, 251.0, 0.0, 0.0, 732.0, 0.0, 0.0]]  ================================================================================

5 一些想法 目前我尝试过多种启发式算法求解该问题，如模拟退火、禁忌搜索和遗传算法。就求解过程来看，禁忌搜索得到最优解的速度最快，基本10步以内就能找到最优解，原因大概是因为所需搜寻的‘山峰’比较少，但随着求解规模的增长，邻域范围变大，禁忌搜索的求解过程可能会变得非常漫长；个人认为退火算法的通用性比较强（自己试验过，退火算法在TSP、VRP、CVRP、VRPTW等问题上都能取得较满意的结果），也有较强的鲁棒性，但是本例中退火过程显得很漫长（一是因为alpha=0.98较大，虽然增加了解的遍历性，但影响了收敛速度；二可能是因为Cal_cost(location) 调用了很多其他函数，得到目标函数值的过程稍显复杂），但求解规模对时间的影响应该会较禁忌搜索小；遗传算法属于群体优化算法，原理比较复杂一些，代码写起来很长，优化速度也不是很理想。 最后，小白第一次写博客，Python掌握的也不熟，所以是抱着一种虚心请教的姿态来一步步写的，当中肯定有代码不简洁、不规范甚至算法理解有偏差的地方，还望大佬们不腻赐教。接下来打算展示用禁忌搜索来求解该问题，有时间就再写下一篇。