本文共 10221 字，大约阅读时间需要 34 分钟。

一.非线性规划的标准型

1.概述

2.例题

3.MATLAB的非线性规划的函数

[x,fval] = fmincon(@fun,x0,A,b,Aeq,beq,lb,ub,@nonlfun,option)

解释：

1. 非线性规划中对于初始值$x$₀的选取非常重要，因为非线性规划的算法求解出来的是一个局部最优解
2. 如果要求“全局最优解”有两种思路：①给定不同的初始值,在里面得到一个最优解,②先用蒙特卡洛模拟,得到一个蒙特卡洛解,然后将这个解作为初始值求最优解
3. $"option"$选项可以给定求解的算法,一共有四种:$interior-point$（内点法）,$sqp$（序列二次规划）,$active-set$（有效算法）以及$trust-region-reflective$（信赖域反射算法）
4. 不同算法有其各自的优缺点和适用情况，我们可以改变求解的算法来看求解的结果是否变好了，（数模比赛中可以尝试下，这可以体现出稳健性）
5. $“@fun”$表示目标函数，我们要编写一个独立的“m文件”储存目标函数

function F = fun(x)   f=end

①fun可以任意取值，符合MATLAB的命名规范就行，注意保存的m文件就是这个名字

②f也可以任意命名，但是返回的f和函数内部的f一致

③这里的x实际上是表示决策变量的向量，其行列方向取决于初始值x

④调用函数：fmincon（@fun，……）求解

6. “@nonlfun”表示非线性部分的约束，我们也编写一个“m文件”

function [c,ceq] = nonlfun1(x)    % 注意：这里的c实际上就是非线性不等式约束，ceq实际上就是非线性等式约束    % 输入值x实际上就是决策变量，由x1和x2组成的一个向量    % 返回值有两个，一个是非线性不等式约束c，一个是非线性等式约束ceq    % nonlfun1是函数名称，到时候会被fmincon函数调用, 可以任意取名，但不能和目标函数fun1重名    % 保存的m文件和函数名称得一致，也要为nonlfun1.m   c =    ceq = []; end

①c，ceq中可能有多个约束，我们写成列向量的形式

②[x,fval] = fmincon(@fun1,x0,A,b,[],[],[][],@nonlfun1,option)

7. 注意要把下标写在括号里
8. 若不存在某种约束，则可用“[]”代替

4.基础例题

function [c,ceq] = nonlfun2(x)    % 非线性不等式约束    c = [-x(1)^2+x(2)-x(3)^2;   % 一定要注意写法的规范，再次强调这里的x是一个向量！不能把x(1)写成x1            x(1)+x(2)^2+x(3)^2-20];    % 非线性等式约束    ceq = [-x(1)-x(2)^2+2;                x(2)+2*x(3)^2-3]; end

【1】默认方法求例1

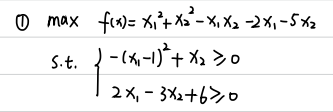
function [c,ceq] = nonlfun1(x)    % 注意：这里的c实际上就是非线性不等式约束，ceq实际上就是非线性等式约束    % 输入值x实际上就是决策变量，由x1和x2组成的一个向量    % 返回值有两个，一个是非线性不等式约束c，一个是非线性等式约束ceq    % nonlfun1是函数名称，到时候会被fmincon函数调用, 可以任意取名，但不能和目标函数fun1重名    % 保存的m文件和函数名称得一致，也要为nonlfun1.m%     -(x1-1)^2 +x2 >= 0    c = [(x(1)-1)^2-x(2)];   % 千万別写成了: (x1-1)^2 -x2   ceq = [];  % 不存在非线性等式约束，所以用[]表示end

function f = fun1(x)    % 注意：这里的f实际上就是目标函数，函数的返回值也是f    % 输入值x实际上就是决策变量，由x1和x2组成的向量    % fun1是函数名称，到时候会被fmincon函数调用, 可以任意取名    % 保存的m文件和函数名称得一致，也要为fun1.m%      max  f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2    f = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2) ; end

%% 例题1的求解% max f(x) = x1^2 +x2^2 -x1*x2 -2x1 -5x2% s.t. -(x1-1)^2 +x2 >= 0 ;  2x1-3x2+6 >= 0x0 = [0 0];  %任意给定一个初始值 A = [-2 3]; b = 6;[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1)  % 注意 fun1.m文件和nonlfun1.m文件都必须在当前文件夹目录下fval = -fval% 一个值得讨论的地方，能不能把线性不等式约束Ax <= b也写到nonlfun1函数中？% 先把nonlfun1中的c改为下面这样：% c = [(x(1)-1)^2-x(2); %        -2*x(1)+3*x(2)-6];%  [x,fval] = fmincon(@fun1,x0,[],[],[],[],[],[],@nonlfun1)% 结果也是可以计算出来的，但并不推荐这样做~

【2】用其他方法求例2

%% 使用其他算法对例题1求解% edit fmincon  % 查看fmincon的“源代码”% Matlab2017a默认使用的算法是'interior-point' 内点法% 使用interior point算法 （内点法）option = optimoptions('fmincon','Algorithm','interior-point')[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)  fval = -fval% 使用SQP算法 （序列二次规划法）option = optimoptions('fmincon','Algorithm','sqp')[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)  fval = -fval   %得到-4.358，远远大于内点法得到的-1,猜想是初始值的影响% 改变初始值试试x0 = [1 1];  %任意给定一个初始值 [x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)  % 最小值为-1，和内点法相同（这说明内点法的适应性要好）fval = -fval  % 使用active set算法 （有效集法）option = optimoptions('fmincon','Algorithm','active-set')[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)fval = -fval  % 使用trust region reflective (信赖域反射算法)option = optimoptions('fmincon','Algorithm','trust-region-reflective')[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option)  fval = -fval  % this algorithm does not solve problems with the constraints you have specified. % 这说明这个算法不适用我们这个约束条件，所以以后遇到了不能求解的情况，记得更换其他算法试试！！！

【3】改变初始值的影响

%% 生成不同的随机初始值来优化代码，有一定几率会触发上面那个Bug，因此不推荐n = 10;  % 重复n次Fval = +inf; X = [0,0];  %初始化最优的结果A = [-2 3]; b = 6;for i = 1:n    x0 = [rand()*10 , rand()*10];  %用随机数生成一个初始值（随机数的范围自己根据题目条件设置）     [x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1,option); % 注意 fun1.m文件和nonlfun1.m文件都必须在当前文件夹目录下    if fval < Fval  % 如果找到了更小的值，那么就代替最优的结果        Fval = fval;        X = x;    endendFval = -FvalX

【4】使用蒙特卡罗的方法来找初始值(推荐）

%% 使用蒙特卡罗的方法来找初始值(推荐）clc,clear;n=10000000; %生成的随机数组数x1=unifrnd(-100,100,n,1);  % 生成在[-100,100]之间均匀分布的随机数组成的n行1列的向量构成x1x2=unifrnd(-100,100,n,1);  % 生成在[-100,100]之间均匀分布的随机数组成的n行1列的向量构成x2fmin=+inf; % 初始化函数f的最小值为正无穷（后续只要找到一个比它小的我们就对其更新）for i=1:n    x = [x1(i), x2(i)];  %构造x向量, 这里千万别写成了：x =[x1, x2]    if ((x(1)-1)^2-x(2)<=0)  & (-2*x1(i)+3*x2(i)-6 <= 0)     % 判断是否满足条件        result = -x(1)^2-x(2)^2 +x(1)*x(2)+2*x(1)+5*x(2) ;  % 如果满足条件就计算函数值        if  result  < fmin  % 如果这个函数值小于我们之前计算出来的最小值            fmin = result;  % 那么就更新这个函数值为新的最小值            x0 = x;  % 并且将此时的x1 x2更新为初始值        end    endenddisp('蒙特卡罗选取的初始值为：'); disp(x0)A = [-2 3]; b = 6;[x,fval] = fmincon(@fun1,x0,A,b,[],[],[],[],@nonlfun1)fval = -fval

【5】其他例题的求解

function f = fun2(x)    %     f = x(1)^2+x(2)^2 +x(3)^2+8 ;     f = sum(x.*x) + 8;  % 可别忘了x实际上是一个向量，我们可以使用矩阵的运算符号对其计算end

function [c,ceq] = nonlfun2(x)    % 非线性不等式约束    c = [-x(1)^2+x(2)-x(3)^2;   % 一定要注意写法的规范，再次强调这里的x是一个向量！不能把x(1)写成x1            x(1)+x(2)^2+x(3)^2-20];    % 非线性等式约束    ceq = [-x(1)-x(2)^2+2;                x(2)+2*x(3)^2-3]; end

%% 例题二的求解x0 = [1 1 1];  %任意给定一个初始值 lb = [0 0 0];  % 决策变量的下界[x,fval] = fmincon(@fun2,x0,[],[],[],[],lb,[],@nonlfun2)  % 注意 fun2.m文件和nonfun2.m文件都必须在当前文件夹目录下% x =%          0.552167405729277          1.20325915507969         0.947824046150443% fval =%           10.6510918606939%% 使用蒙特卡罗的方法来找初始值(推荐）clc,clear;n=1000000; %生成的随机数组数x1= unifrnd(0,2,n,1);   % 生成在[0,2]之间均匀分布的随机数组成的n行1列的向量构成x1x2 = sqrt(2-x1);  % 根据非线性等式约束用x1计算出x2x3 = sqrt((3-x2)/2); % 根据非线性等式约束用x2计算出x3fmin=+inf; % 初始化函数f的最小值为正无穷（后续只要找到一个比它小的我们就对其更新）for i=1:n    x = [x1(i), x2(i), x3(i)];  %构造x向量, 这里千万别写成了：x =[x1, x2, x3]    if (-x(1)^2+x(2)-x(3)^2<=0) & (x(1)+x(2)^2+x(3)^2-20<=0)   % 判断是否满足条件        result =sum(x.*x) + 8 ;  % 如果满足条件就计算函数值        if  result  < fmin  % 如果这个函数值小于我们之前计算出来的最小值            fmin = result;  % 那么就更新这个函数值为新的最小值            x0 = x;  % 并且将此时的x1 x2 x3更新为初始值        end    endenddisp('蒙特卡罗选取的初始值为：'); disp(x0)lb = [0 0 0];  % 决策变量的下界[x,fval] = fmincon(@fun2,x0,[],[],[],[],lb,[],@nonlfun2)  % 注意 fun2.m文件和nonfun2.m文件都必须在当前文件夹目录下

function f = fun3(x)    f = -prod(x);  % 可别忘了x实际上是一个向量（prod表示连乘符号，用法和sum类似）end

%% 例题三的求解(蒙特卡罗模拟那一讲的例题)clear;clc% 蒙特卡罗模拟得到的最大值为3445.6014% 最大值处x1 x2 x3的取值为：%           22.5823101903968          12.5823101903968          12.1265223966757A = [1 -2 -2;  1 2 2];  b = [0 72];x0 = [ 22.58   12.58  12.13];Aeq = [1 -1 0]; beq = 10;lb = [-inf 10 -inf];  ub = [inf 20 inf];  [x,fval] = fmincon(@fun3,x0,A,b,Aeq,beq,lb,ub,[])  % 注意没有非线性约束，所以这里可以用[]替代，或者干脆不写fval = -fval

二.例题

1.选址问题

function f = fun5(xx)  % 注意为了避免和下面的x同号，我们把决策变量的向量符号用xx表示（注意xx的长度为16）    a=[1.25  8.75  0.5  5.75  3  7.25];  % 工地的横坐标    b=[1.25  0.75  4.75	5  6.5  7.25];   % 工地的纵坐标    x = [xx(13)  xx(15)];  % 新料场的横坐标    y = [xx(14)  xx(16)];  % 新料场的纵坐标    c = [];  % 初始化用来保存工地和料场距离的向量 (这个向量就是我们的系数向量）    for  j =1:2        for i = 1:6            c = [c;  sqrt( (a(i)-x(j))^2 + (b(i)-y(j))^2)];  % 每循环一次就在c的末尾插入新的元素        end    end    % 下面我们要求吨千米数，注意c是列向量，我们计算非线性规划时给定的初始值x0是行向量    f = xx(1:12) * c;end

%% 选址问题clear;clcformat long g   %可以将Matlab的计算结果显示为一般的长数字格式（默认会保留四位小数，或使用科学计数法）% % (1) 系数向量（原来线性规划问题的写法,我们只需要在此基础上改动一点就可以了）% a=[1.25  8.75  0.5  5.75  3  7.25];  % 工地的横坐标% b=[1.25  0.75  4.75	5  6.5  7.25];   % 工地的纵坐标% x = [5  2];  % 料场的横坐标% y = [1  7];  % 料场的纵坐标% c = [];  % 初始化用来保存工地和料场距离的向量 (这个向量就是我们的系数向量）% for  j =1:2%     for i = 1:6%         c = [c;  sqrt( (a(i)-x(j))^2 + (b(i)-y(j))^2)];  % 每循环一次就在c的末尾插入新的元素%     end% end% (2) 不等式约束A =zeros(2,16);  % 注意这里要改成16A(1,1:6) = 1;A(2,7:12) = 1;b = [20,20]';% (3) 等式约束Aeq = zeros(6,16);  % 注意这里要改成16for i = 1:6    Aeq(i,i) = 1;  Aeq(i,i+6) = 1;endbeq = [3 5 4 7 6 11]';  % 每个工地的日需求量%（4）上下界lb = zeros(16,1);% lb = [zeros(12,1); -inf*ones(4,1)];  两个新料场坐标的下界可以设为-inf% 进行求解% 注意哦，这里我们只尝试了这一个初始值，大家可以试试其他的初始值，有可能能够找到更好的解。% 未来我会在遗传算法中再来看这个例题。x0 = [3 5 0 7 0 1 0 0 4 0 6 10 5 1 2 7];  % 用第一问的结果作为初始值[x,fval] = fmincon(@fun5,x0,A,b,Aeq,beq,lb)  % 注意没有非线性约束，所以这里可以用[]替代，或者干脆不写reshape(x(1:12),6,2)  % 将x的前12个元素变为6行2列便于观察（reshape函数是按照列的顺序进行转换的，也就是第一列读完，读第二列，即x1对应x_1,1，x2对应x_2,1）% 新坐标（5.74，4.99） （7.25，7.25）% fval =%           89.9231692432933% 第一问的fval =%           135.281541790676135.281541790676 - 89.9231692432933  %  45.3583725473827

2.飞行管理问题

function [c,ceq] = nonlfun6(delta)   % 决策变量delta为六架飞机调整的角度     x = [150 85 150 145 130  0]; % 飞机初始位置的横坐标     y = [140 85 155  50 150  0]; % 飞机初始位置的纵坐标     theta = [243 236 220.5 159 230 52] * pi / 180; % 飞机初始的飞行方向角      v = 800;  % 飞机速度     co = cos(theta + delta);  % 包含6个元素的向量     si = sin(theta + delta);  % 包含6个元素的向量     % 下面开始计算飞机i和j之间的最短距离（只需要计算矩阵的一半即可）     d = zeros(6);  % 初始化飞机两两之间的最短距离矩阵     for i = 2: 6         for j = 1: i-1             % 套用我们推导出来的公式计算飞机i和飞机j相距最近的时间             fenzi = ((y(j)-y(i))*(si(j)-si(i)) +(x(j)-x(i))*(co(j)-co(i))) ;  % 分子             fenmu =  v * ((co(j)-co(i))^2 + (si(j)-si(i))^2);  % 分母             t(i,j) =- fenzi / fenmu;             if t(i,j) <0                   d(i, j) = 1000; % 此时最初的位置就是相距最近的点，因为最初的时候所有飞机两两之间的距离就大于8，因此未来绝不会相撞，我们令它们的距离为一个特别大的数             else                 d(i, j) = sqrt((x(j)-x(i)+v*t(i,j)*(co(j)-co(i)))^2+(y(j)-y(i)+v*t(i,j)*(si(j)-si(i)))^2);              end          end     end     % 非线性不等式约束     c =ones(15,1)*8.000001 - [d(2,1); d(3,1:2)'; d(4,1:3)'; d(5,1:4)'; d(6,1:5)'];       % 12个非线性不等式约束: “最短距离>8” 等价于 “8 - 最短距离<0”     % 注意： 由于Matlab标准型中取的是小于等于号，因此这里取一个比8略大的数：8.000001-最短距离<=0      ceq = [];  % 没有非线性等式约束end

function f = fun6(delta)   % 决策变量delta为六架飞机调整的角度   %         f =sum(abs(delta)) * 180 /  pi;   % 目标函数第一种定义：绝对值的和（将弧度转换为度数）  f = sum(delta .* delta) * (180 /  pi)^2;  % 目标函数第二种定义：平方和（将弧度转换为度数）end

%% 飞行管理问题format long g%%  （1）画六架飞机的位置clear;clcfigure(1)  % 生成一个图形box on  % 显示为封闭的盒子% 绘制飞机的初始位置data = [150	140	243;    85	85	236;    150	155	220.5;    145	50	159;    130	150	230;    0	0	52];plot(data(:,1),data(:,2),'.r')axis([0 160,0,160]);% 设置坐标轴刻度范围hold on;% 在图上标上注释for i = 1:6    txt = ['飞机',num2str(i)];    text(data(i,1)+2,data(i,2)+2,txt,'FontSize',8)end% 把Matlab做出来的图可以导出，然后再放到PPT中画出飞机飞行方向的箭头（就和讲义上的类似）%% 求解非线性规划问题x0 = [0 0 0 0 0 0];  % 初始值lb = -pi/6*ones(6,1);ub = pi/6*ones(6,1);[x,fval] = fmincon(@fun6,x0,[],[],[],[],lb,ub,@nonlfun6)x = x * 180 / pi    % 将弧度转换为度数% 定义一：fval = 3.7315° % 定义二:  fval = 6.9547((°)^2)