本文共 2817 字，大约阅读时间需要 9 分钟。

一.概述

二.用MATLAB求解

三.基础例题

%% 线性整数规划问题%% 例1c=[-20,-10]';intcon=[1,2];  % x1和x2限定为整数A=[5,4;      2,5];b=[24;13];lb=zeros(2,1);  [x,fval]=intlinprog(c,intcon,A,b,[],[],lb)fval = -fval%% 例2c=[18,23,5]';intcon=3;  % x3限定为整数A=[107,500,0;      72,121,65;      -107,-500,0;      -72,-121,-65];b=[50000;2250;-500;-2000];lb=zeros(3,1);[x,fval]=intlinprog(c,intcon,A,b,[],[],lb)%% 例3c=[-3;-2;-1]; intcon=3; % x3限定为整数A=ones(1,3); b=7;Aeq=[4 2 1]; beq=12;lb=zeros(3,1); ub=[+inf;+inf;1]; %x(3)为0-1变量[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)

四.一些实际例题

1.背包问题

%% 背包问题（货车运送货物的问题）c = -[540 200 180 350 60 150 280 450 320 120];  % 目标函数的系数矩阵(最大化问题记得加负号)intcon=[1:10];  % 整数变量的位置(一共10个决策变量，均为0-1整数变量)A = [6 3 4 5 1 2 3 5 4 2];  b = 30;   % 线性不等式约束的系数矩阵和常数项向量（物品的重量不能超过30）Aeq = []; beq =[];  % 不存在线性等式约束lb = zeros(10,1);  % 约束变量的范围下限ub = ones(10,1);  % 约束变量的范围上限%最后调用intlinprog()函数[x,fval]=intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)fval = -fval

2.指派问题

%% 指派问题（选择队员去进行游泳接力比赛）clear;clcc = [66.8 75.6 87 58.6 57.2 66 66.4 53 78 67.8 84.6 59.4 70 74.2 69.6 57.2 67.4 71 83.8 62.4]';  % 目标函数的系数矩阵（先列后行的写法）intcon = [1:20];  % 整数变量的位置(一共20个决策变量，均为0-1整数变量)% 线性不等式约束的系数矩阵和常数项向量（每个人只能入选四种泳姿之一，一共五个约束）A = [1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0;       0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0 0 0 0 0;       0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0 0 0 0 0;       0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 0 0 0 0;       0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1];% A = zeros(5,20);% for i = 1:5%     A(i, (4*i-3): 4*i) = 1;% endb = [1;1;1;1;1];% 线性等式约束的系数矩阵和常数项向量 （每种泳姿有且仅有一人参加，一共四个约束）Aeq = [1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0;          0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0;          0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0;          0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 1];% Aeq = [eye(4),eye(4),eye(4),eye(4),eye(4)];  % 或者写成 repmat(eye(4),1,5)  beq = [1;1;1;1];lb = zeros(20,1);  % 约束变量的范围下限ub = ones(20,1);  % 约束变量的范围上限%最后调用intlinprog()函数[x,fval] = intlinprog(c,intcon,A,b,Aeq,beq,lb,ub)% reshape(x,4,5)'%      0     0     0     1    甲自由泳%      1     0     0     0    乙蝶泳%      0     1     0     0    丙仰泳%      0     0     1     0    丁蛙泳%      0     0     0     0    戊不参加

3.钢管切割

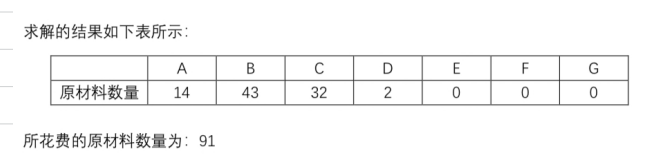
%% 钢管切割问题%% (1)枚举法找出同一个原材料上所有的切割方法for i = 0: 2  % 2.9m长的圆钢的数量    for j = 0: 3  % 2.1m长的圆钢的数量        for k = 0:6   % 1m长的圆钢的数量            if 2.9*i+2.1*j+1*k >= 6 && 2.9*i+2.1*j+1*k <= 6.9                disp([i, j, k])            end        end    endend% 有同学使用比较老的MATLAB版本，会出现浮点数计算的误差% 只需要将上面的if这一行进行适当的放缩即可。% if 2.9*i+2.1*j+1*k >= 6-0.0000001 && 2.9*i+2.1*j+1*k <= 6.9+0.0000001% 有兴趣的同学可以百度下：浮点数计算误差%% (2) 线性整数规划问题的求解c = ones(7,1);  % 目标函数的系数矩阵intcon=[1:7];  %  整数变量的位置(一共7个决策变量，均为整数变量)A = -[1 2 0 0 0 0 1;           0 0 3 2 1 0 1;         4 1 0 2 4 6 1];  % 线性不等式约束的系数矩阵b = -[100 100 100]'; %  线性不等式约束的常数项向量lb = zeros(7,1); % 约束变量的范围下限[x,fval]=intlinprog(c,intcon,A,b,[],[],lb)