本文共 1866 字，大约阅读时间需要 6 分钟。

谈论债券，经常看到“久期”这个概念。

久期（Duration），又称为“持续期”，解释有：

• 是一个很好的衡量债券现金流的指标
• 考量债券时间维度的风险，回收现金流的时间加权平均
• 衡量债券价格对基础利率将变化敏感程度的指标
• 以现金流现值为权重的平均到期时间

有多种不同的形式和解释：

• 麦考莱久期(Macaulay duration)1938

  马考勒久期是使用加权平均数的形式计算债券的平均到期时间。它是债券在未来产生现金流的时间的加权平均,其权重是各期现金值在债券价格中所占的比重。

  对于新手而言，上述语言太难理解，先看两个先导概念：

  • 债券的生命轨迹

    购买债券获得收益的过程：

    1. 投入一笔钱，买入债券；
    2. 按照债券的票面约定，定期获得利息收入；
    3. 等债券到期，将本金以及最后一起的利息一并给我

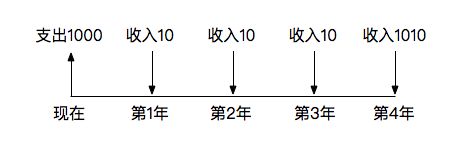
    假设花费1000元购买债券，按照这支债券的约定，债券期限为4年，每年给我10元，最后1年将本金连同最后一期的利息一并给我。

    将债券的声明轨迹表现在时间轴上：

    

  • 钱的时间价值

    1000元在定期存款利率是2%的情况下，1年后就是1020元。

    其中这个1000元称为现值(PV,Private Value),2%称为折现率。

    因此上述债券的现值是：
    $$PV=\frac{10}{1+2\%}+\frac{10}{(1+2\%{)}^2}+\frac{10}{(1+2\%{)}^3}+\frac{1010}{(1+2\%{)}^4}$$

  • 理解麦考莱久期

    如上所述债券的生命周期表明，购买债券只需要关注两个事情：

    1. 每期换多少钱

       债券票面已经规定好了。

    2. 多长时间还完

       此时，麦考莱久期就出现了。其定义为：使用加权平均数的形式计算债券的平均回款时间。从定义中可以看到，麦考莱久期是衡量债券回款时间的指标。

       

       如上三种债券，哪个时间最短呢？对第一种债券，

       1. 用1年时间回款了1040中的10元，对时间1年加一个现金权重$\frac{10}{1040}$；
       2. 用2年时间回款了1040中的10元，对时间2年加一个现金权重$\frac{10}{1040}$；
       3. 用3年时间回款了1040中的10元，对时间3年加一个现金权重$\frac{10}{1040}$；
       4. 用4年时间回款了1040中的1010元，对时间4年加一个现金权重$\frac{1010}{1040}$；

       因此，回款总时间为：
       $$1年\times \frac{10}{1040}+2年\times \frac{10}{1040}+3年\times \frac{10}{1040}+4年\times \frac{1010}{1040}\approx 3.9423年$$
       上述计算未考虑金钱的时间价值，考虑折现率，计算公式为：
       $$1年\times \frac{10/(1+2\%)}{PV}+2年\times \frac{10/(1+2\%{)}^2}{PV}+3年\times \frac{10/(1+2\%{)}^3}{PV}+4年\times \frac{10/(1+2\%{)}^4}{PV}\approx 3.9396$$

       久期，就是以折现现金流为权重的现金回流时间。

• 修正久期(Modified duration)

• 封闭式久期(Closed-form duration)

• 有效久期(Effective duration)

• References