本文共 12549 字，大约阅读时间需要 41 分钟。

1、梯度下降（Gradient Descent，GD）

梯度下降

梯度下降是最流行的优化算法之一并且目前为止是优化神经网络最常见的算法,具有实现简单的优点。

梯度下降是一种以通过在目标函数梯度 的反向上更新模型参数，来最小化模型参数的目标函数$J(\theta )$的方法。

梯度

梯度实际上就是多变量微分的一般化。

下面这个例子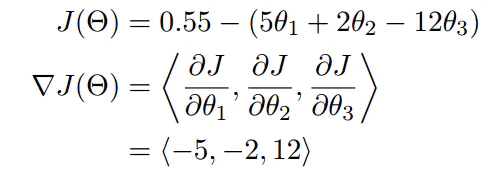： 我们可以看到，梯度就是分别对每个变量进行微分，然后用逗号分割开，梯度是用<>包括起来，说明梯度其实是一个向量。

梯度是微积分中一个很重要的概念，

• 在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率
• 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向

梯度下降的优化思想：

开始时我们随机选择一个参数的组合，计算目标函数，然后用当前位置负梯度方向作为搜索方向（因为该方向为当前位置的最快下降方向），寻找下一个能让目标函数值下降最多的参数组合。我们持续这么做直到找到一个局部最小值（local minimum），因为我们并没有尝试完所有的参数组合，所以不能确定我们得到的局部最小值是否便是全局最小值（global minimum），选择不同的初始参数组合，可能会找到不同的局部最小值。

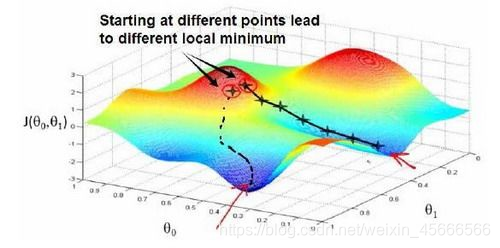
梯度下降算法如下：

• 初始化参数${\Theta }_j$

• 迭代，更新参数${\Theta }_j$：

  ${\Theta }_j:={\Theta }_j-\alpha \frac{\partial J(\Theta )}{\partial {\Theta }_j}$

  其中，$J(\Theta )$为所求目标函数，${\Theta }_j$为参数。

• 终止：可设置最大迭代次数或梯度小于某值。

描述：对$\Theta$更新，使得$J(\Theta )$按梯度下降最快方向进行，一直迭代下去，最终得到局部最小值。其中$\alpha$是学习率（learning rate），它决定了我们沿着能让代价函数下降程度最大的方向向下迈出的步子有多大。

那么我们如何检测参数是否已经收敛了呢？一种是检验两次迭代，如果两次迭代中，是否改变了很多，如果在两次迭代中没怎么改变，我们或许就可以说算法有可能收敛了。另一种，更常用的方法是，检验的值，如果你试图最小化的量不再发生很大的改变时，你也许就可以认为它收敛了。

例子：如果目标函数$J(\Theta )$只有两个参数，如下图所示

参数${\Theta }_1$的更新： 如果导数即此点的斜率为负，负负得正，在原来的基础上增加。 如果导数即此点的斜率为正，负正得负，在原来的基础上减少。

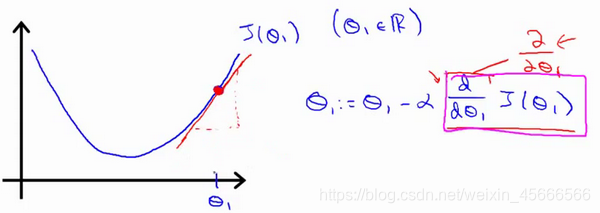
增加或减少的程度不仅仅取决于导数即梯度，还取决于学习率$\alpha$。

学习率$\alpha$ 对移动幅度的影响:

• 学习率$\alpha$如果太小了，只能这样像小宝宝一样一点点地挪动，去努力接近最低点，这样就需要很多步才能到达最低点，所以如果太小的话，可能会很慢，达到收敛所需的迭代次数就会非常高。

• 学习率$\alpha$如果太大，那么梯度下降法可能会越过最低点，甚至可能无法收敛，下一次迭代又移动了一大步，越过一次，又越过一次，一次次越过最低点，直到你发现实际上离最低点越来越远，所以，如果太大，它会导致无法收敛，甚至发散。

  

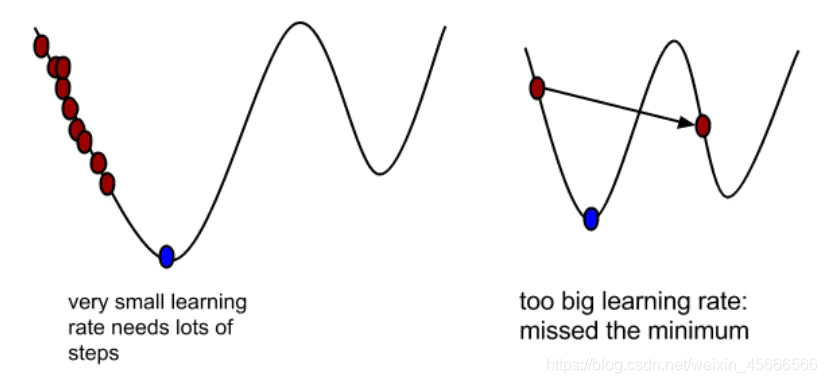
• 即使学习速率$\alpha$保持不变时，梯度下降也可以收敛到局部最低点。因为如果你的参数已经处于局部最低点，也就是说导数为0，那么梯度下降法更新其实什么都没做，它不会改变参数的值。

因此，学习率$\alpha$的选择也是很重要的。

基于学习率的变化以及梯度对于梯度下降的优化效果还是有影响的，因此产生了很多基于学习率调整或者修正梯度估计的优化器用于梯度下降。见。

$J(\Theta )$随着迭代次数的增加变化如下图

图1，2意味着模型应该选择较小的$\alpha$值。

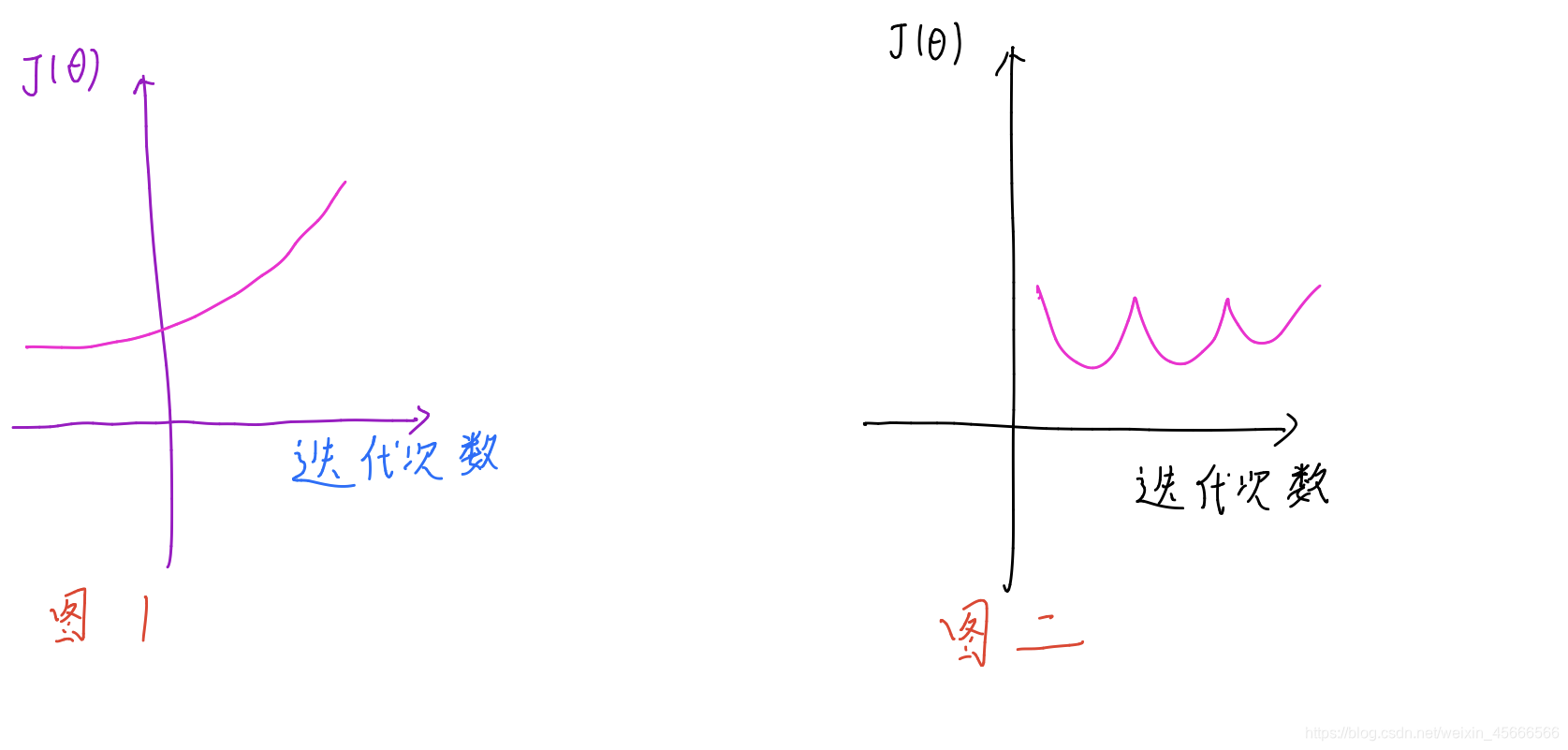
$\alpha$值的尝试一般为0.001，0.003，0.01，0.03，0.1，0.3，1…

梯度下降算法的种类

梯度下降法作为机器学习中较常使用的优化算法，根据每次迭代中梯度更新所用到的训练样本大小即批量大小有以下三种不同的形式：批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）以及小批量梯度下降（Mini-Batch Gradient Descent）。其中小批量梯度下降法也常用在深度学习中，对模型进行训练。他们不同之处在于我们在计算目标函数梯度时所用数据量的多少。依据数据的规模，我们在更新参数的准确性和执行一次更新所用时间之间进行一种折中。

为了便于理解，这里我们将使用只含有一个特征的线性回归来展开。

此时线性回归的假设函数为： $$h_{\theta }(x^{(i)})={\theta }_1{x}^{(i)}+{\theta }_0$$ 其中$i=1,2,...,m$表示样本数.

对应的目标函数（代价函数） 即为：

$$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

---

2、 批量梯度下降（Batch Gradient Descent，BGD）

BGD是最原始的形式也就是GD，它是指在每一次迭代使用所有样本(m个）求梯度并更新参数。

（1）对目标函数求偏导：

$$\frac{\partial J({\theta }_0,{\theta }_1)}{\partial {\theta }_j}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$ （2）每次迭代对参数进行更新： $${\theta }_j:={\theta }_j-\frac{\alpha }{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$

注意这里更新时存在一个求和函数，即为对所有样本进行计算处理，可与下文SGD法进行比较。

伪代码：

for i in range(nb_epochs):#nb_epochs 最大迭代次数  params_grad = evaluate_gradient(loss_function, data, params)  params = params - learning_rate * params_grad

【python-代码实现】

# 定义数据特征和标签的提取函数：def get_fea_lab(train_data):    cols = train_data.shape[1]             # 数据集总列数    X = train_data.iloc[:,0:cols-1]       # X取data中不包括索引列的前两列    y = train_data.iloc[:,cols-1:cols]    # y取data中的最后一列    X = np.matrix(X.values)    y = np.matrix(y.values)    return X,y  # 定义代价函数：以平方损失函数为例，可更改为其他方式def computeCost(train_data,theta):    X,y = get_fea_lab(train_data)      inner = np.power(((X * theta.T) - y), 2)#np.power()多维幂运算    return np.sum(inner) / (2 * len(X))  # 定义批量梯度下降函数：def batch_gradient_descent(train_data,theta,alpha,iters):    X,y = get_fea_lab(train_data)      temp = np.matrix(np.zeros(theta.shape))#初始化参数变量    parameters = int(theta.ravel().shape[1])#待估计参数的个数    cost = np.zeros(iters)#初始化代价函数，一共有iters个        for i in range(iters):#更新参数        error = (X * theta.T) - y#误差                for j in range(parameters):            term = np.multiply(error, X[:,j])#梯度            temp[0,j] = theta[0,j] - ((alpha / len(X)) * np.sum(term))                    theta = temp#最终参数变量取值        cost[i] = computeCost(train_data, theta)#每次更新所对应的代价函数            return theta, cost#返回参数变量，以及代价函数

优点：

• 一次迭代是对所有样本进行计算，此时利用矩阵进行操作，实现了并行。
• 由全数据集确定的方向能够更好地代表样本总体，从而更准确地朝向极值所在的方向。当目标函数为凸函数时，BGD一定能够得到全局最优。

缺点：

• 当样本数目 m很大时，每迭代一步都需要对所有样本计算，训练过程会很慢。

那么，当我们遇到这样非常大的数据集的时候怎么办呢？我们应该使用另一种梯度下降算法——随机梯度算法。

3、 随机梯度下降（Stochastic Gradient Descent，SGD）

随机梯度下降法不同于批量梯度下降，随机梯度下降是每次迭代使用一个样本j来对参数进行更新。使得训练速度加快。

对于一个样本的目标函数为：

$$J^{(i)}({\theta }_0,{\theta }_1)=\frac{1}{2}(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$$

  （1）对目标函数求偏导：

$$\frac{\partial J^{(i)}({\theta }_0,{\theta }_1)}{\partial {\theta }_j}=(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$

  （2）参数更新：

$${\theta }_j:={\theta }_j-\alpha (h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$

注意，这里不再有求和符号

伪代码：

for i in range(nb_epochs):  np.random.shuffle(data)  for example in data:    params_grad = evaluate_gradient(loss_function, example, params)    params = params - learning_rate * params_grad

【python-代码实现】

# 定义数据特征和标签的提取函数：def get_fea_lab(data):    cols = data.shape[1]#数据集总列数      X = data.iloc[:,0:cols-1] # X是data中的前两列(不包括索引列)    y = data.iloc[:,cols-1:cols] # y是data中的最后一列     # 将X和y都转化成矩阵的形式：    X = np.matrix(X.values)    y = np.matrix(y.values)    return X,y # 定义使用第i个样本的代价函数：def computeCost(data,theta,i):    X,y = get_fea_lab(data)    inner = np.power(((X*theta.T)-y),2)    return (float(inner[i]/2)) # 定义随机梯度下降函数：def stochastic_gradient_descent(data,theta,alpha,epoch):        X0,y0 = get_fea_lab(data)  # 提取X和y矩阵    temp = np.matrix(np.zeros(theta.shape))#初始化参数变量    parameters = int(theta.shape[1])#待估计参数变量的总个数    cost = np.zeros(len(X0))    avg_cost = np.zeros(epoch)        for k in range(epoch):#epoch:回合的意思，在随机梯度下降中，epoch为样本个数        new_data = data.sample(frac=1) # 打乱数据，非必要的一步        X,y = get_fea_lab(new_data)  # 提取新的X和y矩阵                for i in range(len(X)):            error = X[i:i+1]*theta.T-y[i]#单个样本的误差            cost[i] = computeCost(new_data,theta,i)#记录每一个样本的代价                    for j in range(parameters):#参数的更新                temp[0,j] = theta[0,j] - alpha*error*X[i:i+1,j]                        theta = temp        avg_cost[k] = np.average(cost)            return theta,avg_cost

随机梯度下降法不同于批量梯度下降，它的具体思路是：算法中对T参数$\Theta$的每次更新不需要再全部遍历一次整个样本，只需要随机选择一个样本进行更新，之后再用下一个样本进行下一次更新，像批量梯度下降一样不断迭代更新。

随机梯度下降相当于在批量梯度下降的梯度上引入了随机噪声。

优点：

• 由于不是在全部训练数据上的损失函数，而是在每轮迭代中，随机优化某一条训练数据上的损失函数，这样每一轮参数的更新速度大大加快，收敛速度也非常快。适用于大规模训练样本情况。

缺点：

• 准确度下降。在非凸优化问题中，随机梯度下降更容易逃离局部最优点。
• 可能会收敛到局部最优，由于单个样本并不能代表全体样本的趋势。
• 无法充分利用计算机的并行计算能力

解释一下为什么SGD收敛速度比BGD要快：

  答：这里我们假设有30W个样本，对于BGD而言，每次迭代需要计算30W个样本才能对参数进行一次更新，需要求得最小值可能需要多次迭代（假设这里是10）；而对于SGD，每次更新参数只需要一个样本，因此若使用这30W个样本进行参数更新，则参数会被更新（迭代）30W次，而这期间，SGD就能保证能够收敛到一个合适的最小值上了。也就是说，在收敛时，BGD计算了 10×30W 次，而SGD只计算了 1×30W 次。

SGD算法的收敛图：

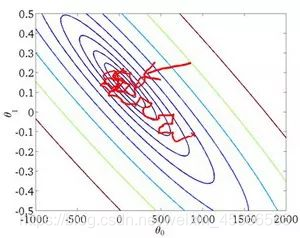
4、 小批量梯度下降（Mini-Batch Gradient Descent, MBGD）

小批量梯度下降算法的核心思想仍然是基于梯度，通过对目标函数中的参数不断迭代更新，使得目标函数逐渐靠近最小值。它是批量梯度下降与随机梯度下降的折中，有着训练过程较快，同时又能保证得到较为精确的训练结果。在一些情况下，小批量梯度下降比批量梯度下降和随机梯度下降的速度都要快。MBGD与BGD唯一区别是每次更新是选取部分训练样本。

其思想是：每次迭代 使用 一小部分训练样本（K个样本）来求梯度并更新参数。

采取K个训练样本则参数的更新公式如下

$${\theta }_j:={\theta }_j-\alpha \frac{1}{K}\sum _{k=i}^{i+K-1}(h_{\theta }(x^{(k)})-y^{(k)})x_j^{(k)}$$

比如选取10个样本，参数更新公式为：

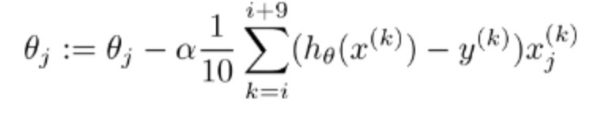伪代码：

for i in range(nb_epochs):  np.random.shuffle(data)  for batch in get_batches(data, batch_size=10):#batch_size为选取的样本数量    params_grad = evaluate_gradient(loss_function, batch, params)    params = params - learning_rate * params_grad

【python-代码实现】

# 定义数据特征和标签的提取函数：def get_fea_lab(train_data):    cols = train_data.shape[1]             # 数据集总列数    X = train_data.iloc[:,0:cols-1]       # X取data中不包括索引列的前两列    y = train_data.iloc[:,cols-1:cols]    # y取data中的最后一列    X = np.matrix(X.values)    y = np.matrix(y.values)        return X,y  # 定义小批量样本的代价函数：def computeCost(train_data,theta,k,mb_size):        X,y = get_fea_lab(train_data)               #取部分样本    X = X[k:k+mb_size]          y = y[k:k+mb_size]     inner = np.power(((X*theta.T)-y),2)    term = np.sum(inner)/(2*mb_size)        return term  #定义小批量梯度下降函数：#训练数据集，参数，学习率，批量大小def mb_gradient_descent(train_data,theta,alpha,batch_size):        X,y = get_fea_lab(train_data)    temp = np.matrix(np.zeros(theta.shape))      # temp用于存放theta参数的值    parameters = int(theta.shape[1])             # parameter用于存放theta参数的个数    m = len(X)                                   # m用于存放数据集中的样本个数    cost = np.zeros(int(np.floor(m/batch_size)))    # cost用于存放代价函数，一共有$m/bantch_size$个    st_posi = list(np.arange(0,m,batch_size))       # st_posi用于存放每次小批量迭代开始的位置    new_st_posi = st_posi[:len(cost)]            # 去掉最后一次小批量迭代开始的位置    k = 0        for i in new_st_posi:                cost[k] = computeCost(train_data,theta,i,batch_size)        k = k + 1        error = (X*theta.T) - y                for j in range(parameters):                        t = np.multiply(error,X[:,j])            term = t[i:i + batch_size]            temp[0,j] = theta[0,j] - (alpha/batch_size)*(np.sum(term))                                    theta = temp                                return theta, cost

优点：

• 通过矩阵运算，每次在一个batch上优化神经网络参数并不会比单个数据慢太多。
• 每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。(比如上例中的30W，设置batch_size=100时，需要迭代3000次，远小于SGD的30W次)
• 可实现并行化。

缺点：

• batch_size的不当选择可能会带来一些问题。

  batcha_size的选择带来的影响：

  • 在合理地范围内，增大batch_size的好处：
    a. 内存利用率提高了，大矩阵乘法的并行化效率提高。
    b. 跑完一次 epoch（全数据集）所需的迭代次数减少，对于相同数据量的处理速度进一步加快。
    c. 在一定范围内，一般来说 Batch_Size 越大，其确定的下降方向越准，引起训练震荡越小。
  • 盲目增大batch_size的坏处：
     a. 内存利用率提高了，但是内存容量可能撑不住了。
     b. 跑完一次 epoch（全数据集）所需的迭代次数减少，要想达到相同的精度，其所花费的时间大大增加了，从而对参数的修正也就显得更加缓慢。
    c. Batch_Size 增大到一定程度，其确定的下降方向已经基本不再变化。

在训练深度神经网络时，训练数据的规模通常比较大。如果在梯度下降时，每次迭代都要计算整个训练数据集上的梯度，这就需要比较多的计算资源。另外大规模训练集中的数据通常会冗余，因此，也没有必要在整个训练集上计算梯度。因此，在计算深度神经网络时，经常会使用小批量梯度下降法。

下图显示了三种梯度下降算法的收敛过程：

---

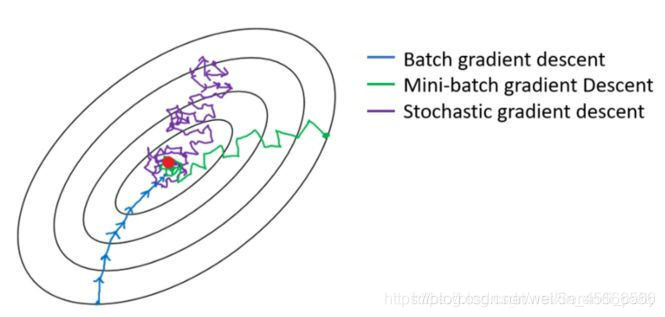
下面利用三种不同的梯度下降法(BGD、SGD、MBGD)求解单变量线性回归模型中的参数，建立线性回归模型；并据此对三种梯度下降进行一个简单的比较。

数据集：参数变量：人口数；目标值：收益。

问题：基于人口数与收益建立单变量线性回归模型，以预测收益。

先导入要用到的各种包：

%matplotlib notebookimport pandas as pdimport numpy as npimport matplotlib.pyplot as plt

加载数据并查看数据的相关信息：

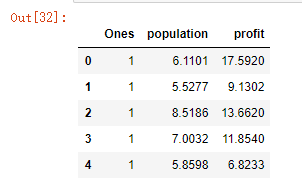
df = pd.read_csv('ex1data1.txt',header=None,names=['population', 'profit'])#读取数据并赋予列名df.head()#查看前五行

population profit

0 6.1101 17.5920

1 5.5277 9.1302

2 8.5186 13.6620

3 7.0032 11.8540

4 5.8598 6.8233

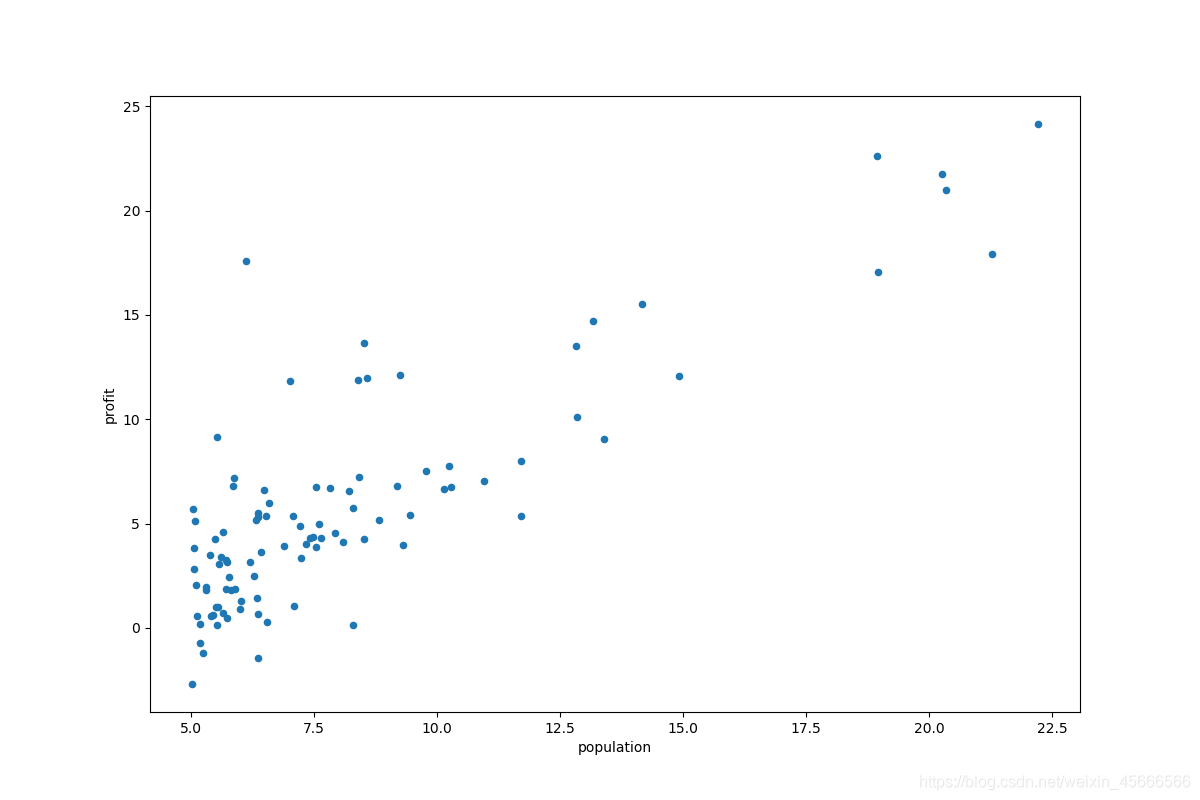
查看数据分布，散点图

df.plot(kind='scatter',x='population',y='profit',figsize=(12,8))

通过数据集的散点图分布，可对此数据集建立线性回归模型：

建立一个简单的线性回归方程y=b+ax，然后以此方程为基础，希望能通过人口这一变量对其收益有一个大致的预测。

下面分别利用三种不同的梯度下降方法求解线性回归方程中的未知参数：

第一步：数据预处理

向量化：在原数据集中添加一列1

df.insert(0, 'Ones', 1)#向量化：$\theta_0X_0$中X_0等于1df.head()

(一)利用批量梯度下降

# 初始化相关参数：theta = np.matrix(np.array([0,0]))alpha = 0.0001iters = 1000  # 调用批量梯度下降函数求解回归方程中的未知数theta#g:参数，cost：代价函数g, cost1 = batch_gradient_descent(df, theta, alpha, iters)g # g就是参数theta，其值为(matrix([[0.00868908, 0.80057917]]),

绘制代价函数具体值与迭代次数的关系图像：

fig, axes = plt.subplots()axes.plot(np.arange(iters), cost1, 'r')axes.set_xlabel('Iterations')axes.set_ylabel('Cost')axes.set_title('Error vs. Training iters')fig.savefig('p3.png')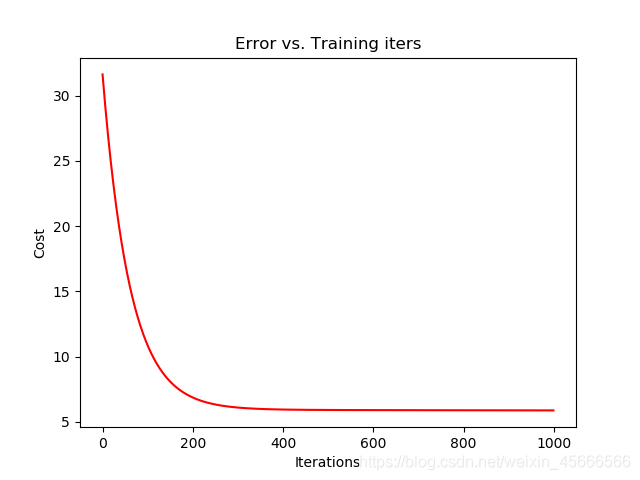

(二)利用随机梯度下降

# 初始化学习率、迭代轮次和参数theta：alpha = 0.000001epoch = 97#样本个数theta = np.matrix(np.array([0,0])) # 调用随机梯度下降函数来计算线性回归中的theat参数：g,avg_cost = stochastic_gradient_descent(df,theta,alpha,epoch)g # g的值为matrix([[0.03621175, 0.42822426]])

绘制每轮迭代中代价函数的平均值与迭代轮次的关系图像：

fig, axes = plt.subplots()axes.plot(np.arange(epoch), avg_cost, 'r')axes.set_xlabel('Epoch')axes.set_ylabel('avg_cost')axes.set_title('avg_cost vs. Epoch')fig.savefig('p2.png')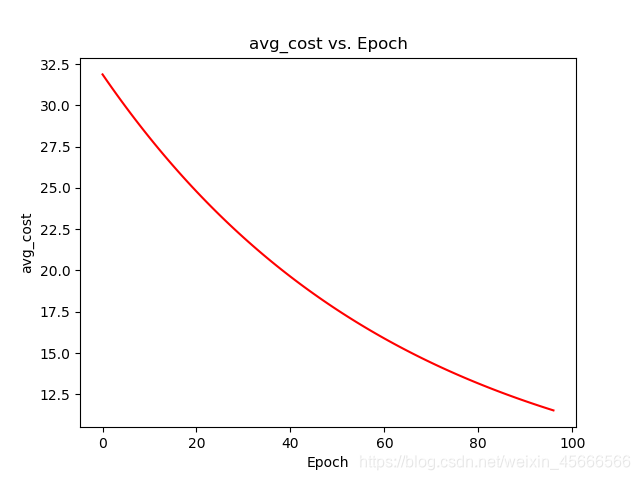

(三)利用小批量梯度下降

# 初始化相关参数：theta = np.matrix(np.array([0,0]))alpha = 0.00001batch_size = 10  # 调用随机梯度下降函数来计算线性回归中的theat参数：#new_data = data.sample(frac=1)  # 打乱数据，没有这一步也可以g,cost2 = mb_gradient_descent(df,theta,alpha,batch_size)g# g的值为(matrix([[0.00053899, 0.00609298]]),

绘制代价函数具体值与迭代次数的关系图像：

fig, axes = plt.subplots()axes.plot(np.arange(len(cost2)), cost2, 'r')axes.set_xlabel('iters')axes.set_ylabel('cost')axes.set_title('cost vs. iters')fig.savefig('p2.png')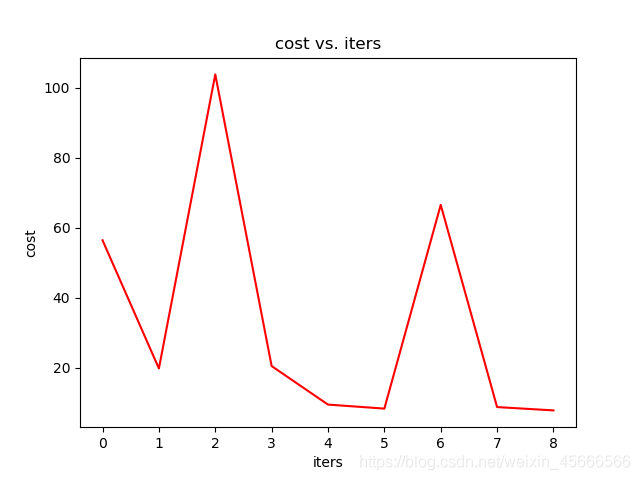

由于数据量小，故使用小批量梯度下降，效果并不太好。

总结：对于求解基于某个数据集而建立起来的线性回归方程中的未知参数：如果该数据集比较小，同时要求最后计算出的参数结果比较精确，此时更适合选择使用批量梯度下降算法。如果该数据集非常大，可以选择采用随机梯度下降，也可以选用小批量梯度下降，视具体情况而定。总的来说，SGD的速度比BGD要快，而且能保证得到一个可以接受的计算结果。而MBGD计算结果的准确程度在BGD和SGD二者之间，但值得指出的是，在一些情况下，MBGD的速度比BGD和SGD都要快，比如本文中的示例，基于得到大致相同的计算结果，在每次迭代更新利用50个样本计算代价函数的情况下，MBGD只需迭代几十次最终就能得到想要的结果。

参考资料：

1、https://ruder.io/optimizing-gradient-descent/index.html#shufflingandcurriculumlearning 2、机器学习课程 3、https://www.jianshu.com/p/c7e642877b0e