
本文共 9215 字,大约阅读时间需要 30 分钟。
文章目录
一、变量之间的线性关系
- “线性”这个词用于描述不同事物时有着不同的含义。
- 我们
最常使用的线性是指“变量”之间的线性关系(linear relationship),它表示两个变量之间的关系可以展示为一条直线,即可以使用方程y=ax+b来进行拟合。 - 要探索两个变量之间的关系是否是线性的,最简单的方式就是绘制散点图,如果散点图能够相对均匀地分布在一条直线的两端,则说明这两个变量之间的关系是线性的。因此,三角函数(如sin(x)),高次函数(y=ax³+b,(a≠0)),指数函数(y=eⁿ)等等图像不为直线的函数所对应的自变量和因变量之间是非线性关系(non–linear relationship)。y=ax+b因此被称为线性方程或线性函数(linear function);三角函数,高次函数等也因此被称为非线性函数(non-linear function)。

二、线性数据与非线性数据
从线性关系这个概念出发,我们有了一种说法叫做“线性数据”。通常来说,一组数据由多个特征和标签组成。当这些特征分别与标签存在线性关系的时候,我们就说这一组数据是线性数据。当特征矩阵中任意一个特征与标签之间的关系需要使用三角函数,指数函数等函数来定义,则我们就说这种数据叫做“非线性数据”。对于线性和非线性数据,最简单的判别方法就是利用模型来帮助我们 ---- 如果是做分类则使用逻辑回归,如果做回归则使用线性回归,如果效果好那数据是线性的,效果不好则数据不是线性的。当然,也可以降维后进行绘图,绘制出的图像分布接近一条直线,则数据就是线性的。

 通常情况下,在进行分类的时候,所用到的数据集往往分布不均匀,甚至还有交叉,如下图所示:
通常情况下,在进行分类的时候,所用到的数据集往往分布不均匀,甚至还有交叉,如下图所示: 
可以看得出,这些数据都不能由一条直线来进行拟合,他们也没有均匀分布在某一条线的周围,那我们怎么判断,这些数据是线性数据还是非线性数据呢?在这里就要注意了,当我们在回归中绘制图像时,绘制的是特征与标签的关系图,横坐标是特征,纵坐标是标签,我们的标签是连续型的,所以我们可以通过是否能够使用一条直线来拟合图像判断数据究竟属于线性还是非线性。然而在分类中,我们绘制的是数据分布图,横坐标是其中一个特征,纵坐标是另一个特征,标签则是数据点的颜色。因此在分类数据中,我们使用“是否线性可分(linearly separable)这个概念来划分分类数据集。当分类数据的分布上可以使用一条直线来将两类数据分开时,我们就说数据是线性可分的。反之,数据不是线性可分的。
三、线性模型与非线性模型
在回归中,线性数据可以使用如下的方程来进行拟合:
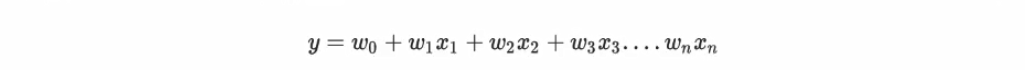 也就是我们的线性回归的方程。根据线性回归的方程,我们可以拟合出一组参数w,在这一组固定的参数下我们可以建立一个模型,而这个模型就被我们称之为是线性回归模型。所以
也就是我们的线性回归的方程。根据线性回归的方程,我们可以拟合出一组参数w,在这一组固定的参数下我们可以建立一个模型,而这个模型就被我们称之为是线性回归模型。所以建模的过程就是寻找参数的过程。此时此刻我们建立的线性回归模型,是一个用于拟合线性数据的线性模型。作为线性模型的典型代表,我们可以从线性回归的方程中总结出线性模型的特点:其自变量都是一次项。 那线性回归在非线性数据上的表现如何呢我们来建立一个明显是非线性的数据集,并观察线性回归和决策树的而回归在拟合非线性数据集时的表现:
- 借助sin(x)生成一组数据集
import numpy as npimport matplotlib.pyplot as pltfrom sklearn.linear_model import LinearRegressionfrom sklearn.tree import DecisionTreeRegressorrnd = np.random.RandomState(42) # 色值随机中子数x = rnd.uniform(-3,3,size=100) # 从-3-3中任意取出100个随机数# 先使用numpy中的函数生成一个sin函数图像,然后人为添加噪音y = np.sin(x) + rnd.normal(size=len(x))/3 # random.normal()生成size个服从正态分布的随机数# 绘制散点图观察数据集形态plt.scatter(x,y,marker='o',c='k',s=20)plt.show()

- 转换数据集形态:sklearn只接受二维以上的数组作为特征矩阵的输入
# 转换数据集形态:sklearn只接受二维以上的数组作为特征矩阵的输入print(x.shape) # (100,)x = x.reshape(-1,1)print(x.shape) # (100, 1)
- 使用原始数据进行建模:线性回归、决策树
# 使用原始数据进行建模LinearR = LinearRegression().fit(x,y)TreeR = DecisionTreeRegressor(random_state=0).fit(x,y)# 创建测试数据进行预测line = np.linspace(-3,3,1000,endpoint=False).reshape(-1,1)# 设置画布fig,ax1 = plt.subplots(1)# 将测试数据放入模型预测ax1.plot(line,LinearR.predict(line),linewidth=2,color='green',label='linear regression')ax1.plot(line,TreeR.predict(line),linewidth=2,color='red',label='decision tree')# 绘制原数据的拟合曲线ax1.plot(x[:,0],y,'o',c='k')ax1.legend(loc='best')ax1.set_ylabel("Regression output")ax1.set_xlabel("Input feature")ax1.set_title("Result before discretization")plt.tight_layout()plt.show() 
决策树无法写作一个线性方程,它是一个典型的非线性模型,当它被用于拟合非线性数据,可以发挥奇效。其他典型的非线性模型还包括使用高斯核的支持向量机树的集成算法,以及一切通过三角函数,指数函数等非线性方程来建立的模型。
根据这个思路,我们也许可以这样推断:线性模型用于拟合线性数据,非线性模型用于拟合非线性数据。但事实上机器学习远远比我们想象的灵活得多,线性模型可以用来拟合非线性数据,而非线性模型也可以用来拟合线性数据,更神奇的是,有的算法没有模型也可以处理各类数据,而有的模型可以既可以是线性,也可以是非线性模型!
四、非线性模型拟合线性数据 & 线性模型拟合非线性数据
-
非线性模型能够拟合或处理线性数据的例子非常多,诸如决策树、随机森林等算法在分类中处理线性可分的数据的效果。无一例外的,非线性模型们几乎都可以在线性可分数据上有不逊于线性模型的表现。同样的,如果我们使用随机森林来拟合一条直线,那随机森林毫无疑问会过拟合,因为线性数据对于非线性模型来说太过简单,很容易就把训练集上的R²训练得很高,MSE训练的很低。

-
但是相反的,线性模型若用来拟合非线性数据或者对非线性可分的数据进行分类,那通常都会表现糟糕。通常如果我们已经发现数据属于非线性数据,或者数据非线性可分的数据,则我们不会选择使用线性模型来进行建模。改善线性模型在非线性数据上的效果的方法之一是进行分箱,并且从下图来看分箱的效果不是一般的好,甚至高过一些非线性模型。=但很容易注意到,在没有其他算法或者预处理帮忙的情况下,线性模型在非线性数据上的表现时很糟糕的。
 从上面的图中,我们可以观察出一个特性:
从上面的图中,我们可以观察出一个特性:线性模型们的决策边界都是一条条平行的直线,而非线性模型们的决策边界是交互的直线(格子),曲线,环形等等。对于分类模型来说,这是我们判断模型是线性还是非线性的重要评判因素:线性模型的决策边界是平行的直线,非线性模型的决策边界是曲线或者交叉的直线。之前我们提到,模型上如果自变量上的最高次方为1,则模型是线性的,但这种方式只适用于回归问题。分类模型中,我们很少讨论模型是否线性,因为我们很少使用线性模型来执行分类任务(逻辑回归是一个特例)。但从上面我们总结出的结果来看,我们可以认为对分类问题而言,如果一个分类模型的决策边界上自变量的最高次方为1,则我们称这个模型是线性模型。 -
对于有一些模型来说,他们既可以处理线性模型又可以处理非线性模型,比如说强大的支持向量机。支持向量机的前身是感知机模型,朴实的感知机模型是实打实的线性模型(其决策边界是直线),在线性可分数据上表现优秀,但在非线性可分的数据上基本属于无法使用状态。
但支持向量机就不一样了。支持向量机本身也是处理线性可分数据的,但却可以通过对数据进行升维(将数据x转移到高维空间Φ中),将非线性可分数据变成高维空间中的线性可分数据,然后使用相应的“核函数”来求解。当我们选用线性核函数"linear"的时候,数据没有进行变换,支持向量机中就是线性模型,此时它的决策边界是直线。而当我们选用非线性核函数比如高斯径向基核函数的时候,数据进行了升维变化,此时支持向量机就是非线性模型,此时它的决策边界在二维空间中是曲线所以这个模型可以在线性和非线性之间自由切换,一切取决于它的核函数。 还有更加特殊的,没有模型的算法,比如最近邻算法KNN,但是能够直接预测出标签或做出判断的算法。而这些算法,并没有线性非线性之分,单纯的是不建模的算法。
还有更加特殊的,没有模型的算法,比如最近邻算法KNN,但是能够直接预测出标签或做出判断的算法。而这些算法,并没有线性非线性之分,单纯的是不建模的算法。

五、使用分箱处理非线性问题 ---- 离散化
让线性回归在非线性数据上表现提升的核心方法之一是对数据进行分箱,也就是离散化。与线性回归相比,我们常用的一种回归是决策树的回归。上文拟合过一条带有噪音的正弦曲线来展示多元线性回归与决策树的差异。
- 使用分箱处理数据:
import numpy as npimport pandas as pdimport matplotlib.pyplot as pltfrom sklearn.preprocessing import KBinsDiscretizerrnd = np.random.RandomState(42) # 色值随机中子数x = rnd.uniform(-3,3,size=100) # 从-3-3中任意取出100个随机数x = x.reshape(-1,1)# 先使用numpy中的函数生成一个sin函数图像,然后人为添加噪音y = np.sin(x) + rnd.normal(size=len(x))/3 # random.normal()生成size个服从正态分布的随机数# 将数据分箱# n_bins 连续型数据分出几箱# encode 模式选择使用哑变量方式做离散化,返回一个稀疏的矩正(m,n_bins),每列是一个特征中的一个类别,# 对于每一个样本而言,含有本类别样本显示0;不含有显示为0enc = KBinsDiscretizer(n_bins=10,encode="onehot") # 建立分箱模型x_binned = enc.fit_transform(x) # 对数据集进行模型训练、分箱处理df_x_binned = pd.DataFrame(x_binned.toarray())
n_bins连续型数据分出几箱encode模式选择使用哑变量方式做离散化,返回一个稀疏的矩正(m,n_bins),m表示数据的总数目。每列是一个特征中的一个类别,对于每一个样本而言,横向来看,属于哪一分箱的对应分箱下计数为1;反之为0。
- 使用线性回归处理分箱后的数据:
'''注意以下代码会报错:因为x_binned和y的数据结构不匹配x_binned => (100,100)line => (1000,)所以,对于测试数据集,我们也应当对其进行分箱处理# 使用线性回归训练分箱处理后的数据Linear_ = LinearRegression().fit(df_x_binned,y) # 对line测试数据集进行预测y_predict = Linear_.predict(line)'''# 分箱处理测试集line_binned = enc.transform(line)df_line_binned = pd.DataFrame(line_binned.toarray()) #(1000,10)# 使用线性回归训练分箱处理后的数据Linear_ = LinearRegression().fit(df_x_binned,y)# 对line测试数据集进行预测y_predict = Linear_.predict(line_binned) # (1000,)
- 可视化处理:
# 使用原始数据进行建模LinearR = LinearRegression().fit(x,y)TreeR = DecisionTreeRegressor(random_state=0).fit(x,y)# 使用分箱数据建模LinearR_ = LinearRegression().fit(x_binned,y)print(LinearR_.score(line_binned,np.sin(line))) # 0.8901529141025571TreeR_ = DecisionTreeRegressor(random_state=0).fit(x_binned,y)# 设置画布fig,(ax1,ax2) = plt.subplots(ncols=2, sharey=True, # 两图共享y轴 figsize=(10,4) )# 将测试数据放入模型预测ax1.plot(line,LinearR.predict(line),linewidth=2,color='green',label='linear regression')ax1.plot(line,TreeR.predict(line),linewidth=2,color='red',label='decision tree')# 绘制原数据的拟合曲线ax1.plot(x[:,0],y,'o',c='k')ax1.legend(loc='best')ax1.set_ylabel("Regression output")ax1.set_xlabel("Input feature")ax1.set_title("Result before discretization")plt.tight_layout()# 将测试数据放入模型预测ax2.plot(line,LinearR_.predict(line_binned),linewidth=2,color='green',label='linear regression',linestyle="-")ax2.plot(line,TreeR_.predict(line_binned),linewidth=2,color='red',label='decision tree',linestyle=":")# 绘制箱宽竖线ax2.vlines(enc.bin_edges_[0], # x轴 *plt.gca().get_ylim(), # y轴的范围 linewidth=1, # 线宽 alpha=0.2 # 透明度 )# 绘制原数据的拟合曲线ax2.plot(x[:,0],y,'o',c='k')ax2.legend(loc='best')ax2.set_xlabel("Input feature")ax2.set_title("Result after discretization")plt.tight_layout()plt.show() 从图像上可以看出,离散化后线性回归和决策树上的预测结果完全相同了 ---- 线性回归比较成功地拟合了数据的分布,而决策树的过拟合效应也减轻了。由于特征矩阵被分箱,因此特征矩阵在每个区域内获得的值是恒定的,因此所有模型对同一个箱中所有的样本都会获得相同的预测值。与分箱前的结果相比线性回归明显变得更加灵活,而决策树的过拟合问题也得到了改善,通过打印R²指数也可以看出来,达到了0.8 。但注意,一般来说我们是不使用分箱来改善决策树的过拟合问题的,因为树模型带有丰富而有效的剪枝功能来防止过拟合。

七、选取最优箱子数
# 选取最优箱子数pred,score,var = [],[],[]bins_range = [2,5,10,15,20,30]for i in bins_range: # 实例化分箱 enc = KBinsDiscretizer(n_bins=i,encode="onehot") # 转换数据 x_binned = enc.fit_transform(x) line_binned = enc.transform(line) # 建立模型 LinearR_ = LinearRegression() # 全数据集上的交叉验证 cvs_result = CVS(LinearR_,x_binned,y,cv=5) score.append(cvs_result.mean()) # 获取五折交叉验证的均值 --- 准确性 var.append(cvs_result.var()) # 获取五折交叉验证的方差 --- 稳定性 # 测试数据集上的打分结果 pred.append(LinearR_.fit(x_binned,y).score(line_binned,np.sin(line)))# 绘制图像plt.figure(figsize=(6,5))plt.plot(bins_range,pred,c='orange',label='test') # 测试数据集R²指数(评分情况)plt.plot(bins_range,score,c='k',label='full data') # 全数据集上的交叉验证结果plt.plot(bins_range,score+np.array(var)*0.5,c='red',linestyle='--',label="var") # 上下环绕交叉验证的均值plt.plot(bins_range,score-np.array(var)*0.5,c='red',linestyle='--')plt.legend()plt.show()
当箱子数为10的时候,测试集和全数据集的评分都较高;当箱子数趋近15时,测试集评分升高,但是全数据集评分有所降低;当箱子数为20左右的时候,测试数据集评分开始下降,但是全数据集评分有所上升,并且此时全数据集的交叉验证效果最好,且两边的方差都较低(上下两条方差线离均值线近)。

- 当箱子数n_bins=20时:
# 创建分箱模型enc = KBinsDiscretizer(n_bins=20,encode="onehot")x_binned = enc.fit_transform(x)line_binned = enc.transform(line)# 使用分箱数据建模LinearR_ = LinearRegression().fit(x_binned,y)print(LinearR_.score(line_binned,np.sin(line))) # 0.9566086751329097TreeR_ = DecisionTreeRegressor(random_state=0).fit(x_binned,y)# 创建画布fig1,ax3 = plt.subplots(1,figsize=(5,4))# 将测试数据放入模型预测ax3.plot(line,LinearR_.predict(line_binned),linewidth=2,color='green',label='linear regression',linestyle="-")ax3.plot(line,TreeR_.predict(line_binned),linewidth=2,color='red',label='decision tree',linestyle=":")# 绘制箱宽竖线ax3.vlines(enc.bin_edges_[0], # x轴 *plt.gca().get_ylim(), # y轴的范围 linewidth=1, # 线宽 alpha=0.2 # 透明度 )# 绘制原数据的拟合曲线ax3.plot(x[:,0],y,'o',c='k')ax3.legend(loc='best')ax3.set_xlabel("Input feature")ax3.set_title("Result after discretization")plt.tight_layout()plt.show() 可以看到模型评分达到了0.95之高,可以说明箱数为20姑且是最优箱数~

发表评论
最新留言
关于作者
