本文共 8994 字，大约阅读时间需要 29 分钟。

1. 如何检测两组数据是否同分布
   

1. 介绍一下BN和LN？有什么差异？LN是在哪个维度上进行归一化？
2. 代码实现卷积操作

class Conv2D(nn.Module):	def __init__(self, kernel_size):		super(Conv2D, self).__init__()		self.weight = nn.Parameter(torch.randn(kernel_size))		self.bias = nn.Parameter(torch.randn(1))	def forward(self, x):		return corr2d(x, self.weight) + self.biasimport torchfrom torch import nndef corr2d(X, K):	h, w = K.shape	Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))	for i in range(Y.shape[0]):		for j in range(Y.shape[1]):			Y[i, j] = (X[i: i + h, j: j + w] * K).sum()	return Y

1. NMS原理
   注意 NMS 是针对一个特定的类别进行操作的。例如假设一张图中有要检测的目标有“人脸”和“猫”，没做NMS之前检测到10个目标框，每个目标框变量表示为: $[x_1,y_1,x_2,y_2,scor{e}_1,scor{e}_2]$ ，其中 $(x_1,y_1)$ 表示该框左上角坐标，$(x_2,y_2)$ 表示该框右下角坐标，$scor{e}_1$ 表示"人脸"类别的置信度，$scor{e}_2$ 表示"猫"类别的置信度。当 $scor{e}_1$ 比 $scor{e}_2$ 大时，将该框归为“人脸”类别，反之归为“猫”类别。最后我们假设10个目标框中有6个被归类为“人脸”类别。

接下来演示如何对“人脸”类别的目标框进行 NMS 。

首先对6个目标框按照 $scor{e}_1$ 即置信度降序排序：

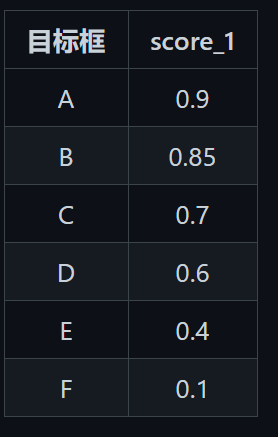取出最大置信度的那个目标框 A 保存下来 (2) 分别判断 B-F 这５个目标框与 A 的重叠度 IOU ，如果 IOU 大于我们预设的阈值（一般为 0.5），则将该目标框丢弃。假设此时丢弃的是 C和 F 两个目标框，这时候该序列中只剩下 B D E 这三个。 (3) 重复以上流程，直至排序序列为空。

# bboxees维度为 [N, 4]，scores维度为 [N, 1]，均为np.array()def single_nms(self, bboxes, scores, thresh = 0.5):    # x1、y1、x2、y2以及scores赋值    x1 = bboxes[:, 0]    y1 = bboxes[:, 1]    x2 = bboxes[:, 2]    y2 = bboxes[:, 3]        # 计算每个检测框的面积    areas = (x2 - x1 + 1) * (y2 - y1 + 1)         # 按照 scores 置信度降序排序, order 为排序的索引    order = scores.argsort() # argsort为python中的排序函数，默认升序排序    order = order[::-1] # 将升序结果翻转为降序        # 保留的结果框索引    keep = []        # torch.numel() 返回张量元素个数    while order.size > 0:        if order.size == 1:            i = order[0]            keep.append(i)            break        else:            i = order[0]  # 在pytorch中使用item()来取出元素的实值，即若只是 i = order[0]，此时的 i 还是一个 tensor，因此不能赋值给 keep            keep.append(i)                    # 计算相交区域的左上坐标及右下坐标        xx1 = np.maximum(x1[i], x1[order[1:]])        yy1 = np.maximum(y1[i], y1[order[1:]])        xx2 = np.minimum(x2[i], x2[order[1:]])        yy2 = np.minimum(y2[i], y2[order[1:]])                # 计算相交的面积，不重叠时为0        w = np.maximum(0.0, xx2 - xx1 + 1)        h = np.maximum(0.0, yy2 - yy1 + 1)        inter = w * h                # 计算 IOU = 重叠面积 / (面积1 + 面积2 - 重叠面积)        iou = inter / (areas[i] + areas[order[1:]] - inter)                # 保留 IOU 小于阈值的 bboxes        inds = np.where(iou <= thresh)[0]        if inds.size == 0:            break        order = order[inds + 1] # 因为我们上面求iou的时候得到的结果索引与order相比偏移了一位，因此这里要补回来    return keep  # 这里返回的是bboxes中的索引，根据这个索引就可以从bboxes中得到最终的检测框结果

1. ReLU函数在0处不可导，为什么在深度学习网络中还这么常用?
   其实我们可以人为提供一个伪梯度，例如给它定义在0处的导数为0，其实tensorflow在实现ReLU的时候也是定义ReLU在0处的导数为0的。
   另外还有一个方法是使用 $ln(1+e^x)$ 来近似，这个函数是连续的，它在0点的导数是0.5。也就是相当于relu在0点的导数取为0.5，也正好是0和1的均值。
2. 池化层的作用以及如何反向传播
   CNN一般采用average pooling或max pooling来进行池化操作，而池化操作会改变feature map的大小，例如大小为64×64的feature map使用2×2的步长池化后，feature map大小为32×32。因此，这会使得在反向传播中，pooling层的梯度无法与前一层相对应。

那怎么解决这个问题呢？其实也很简单，可以理解为就是pooling操作的一个逆过程，把一个像素的梯度传递给4个像素，保证传递的loss（或梯度）总和不变。下面分别来看average pooling和max pooling的反向传播操作过程。

两种pooling层的原理其实很容易就理解了，那它的作用又是什么呢， CNN中为什么要加pooling层？下面汇总一下几位大佬的解释：

1、增加非线性

2、保留主要的特征同时减少参数(降维，效果类似PCA)和计算量，防止过拟合，提高模型泛化能力

3、invariance(不变性)，这种不变性包括translation(平移)，rotation(旋转)，scale(尺度)

1. 在将图像输入到深度学习网络之前，一般先对图像进行预处理，即图像归一化，为什么需要这么做呢？
   图像深度学习网络也是使用gradient descent来训练模型的，使用gradient descent的都要在数据预处理步骤进行数据归一化，主要原因是，根据反向传播公式： $$\frac{\partial J}{{\omega }_{11}}=x_1\ast 后面层梯度的乘积$$ 如果输入层 x 很大，在反向传播时候传递到输入层的梯度就会变得很大。梯度大，学习率就得非常小，否则会越过最优。在这种情况下，学习率的选择需要参考输入层数值大小，而直接将数据归一化操作，能很方便的选择学习率。在未归一化时，输入的分布差异大，所以各个参数的梯度数量级不相同，因此，它们需要的学习率数量级也就不相同。对 w1 适合的学习率，可能相对于 w2 来说会太小，如果仍使用适合 w1 的学习率，会导致在 w2 方向上走的非常慢，会消耗非常多的时间，而使用适合 w2 的学习率，对 w1 来说又太大，搜索不到适合 w1 的解。
   那么深度学习中在训练网络之前应该怎么做图像归一化呢？有两种方法：

归一化到 0 - 1：因为图片像素值的范围都在0~255，图片数据的归一化可以简单地除以255. 。 (注意255要加 . ，因为是要归一化到double型的 0-1 )

归一化到 [-1, 1]：在深度学习网络的代码中，将图像喂给网络前，会先统计训练集中图像RGB这3个通道的均值和方差，如：mean=[123.675, 116.28, 103.53], std=[58.395, 57.12, 57.375]，接着对各通道的像素做减去均值并除以标准差的操作。不仅在训练的时候要做这个预处理，在测试的时候，同样是使用在训练集中算出来的均值与标准差进行的归一化。 注意两者的区别：归一化到 [-1, 1] 就不会出现输入都为正数的情况，如果输入都为正数，会出现什么情况呢？：根据求导的链式法则，w的局部梯度是X，当X全为正时，由反向传播传下来的梯度乘以X后不会改变方向，要么为正数要么为负数，也就是说w权重的更新在一次更新迭代计算中要么同时减小，要么同时增大。

1. 优化函数
   假设当前时刻待优化的参数为 ${\theta }_t$ ，损失函数为 $J(\theta )$ ，学习率为 $\eta$ ，参数更新的框架为：

计算损失函数关于当前参数的梯度：$g_t=\nabla J({\theta }_t)$

根据历史梯度计算一阶动量和二阶动量： $$m_t=\varphi (g_1,g_2,...,g_t)V_t=\psi (g_1,g_2,...,g_t)$$ 即一阶动量为包含当前梯度在内的历史梯度的一次函数，而二阶动量是历史梯度的二次函数。

计算当前时刻的下降梯度： $$\Delta {\theta }_t=-\eta \ast \frac{m_t}{\sqrt{V_t}}$$

根据下降梯度更新参数：${\theta }_{t+1}={\theta }_t+\Delta {\theta }_t$

首先计算一阶动量：（注意这个公式中 $g_t$ 前面的系数与Momentum是不同的） $$m_t={\beta }_1{m}_{t-1}+(1-{\beta }_1)g_t$$ 然后类似 RMSProp 和 AdaDelta 计算二阶动量： $$v_{t,i}={\beta }_2{v}_{t-1,i}+(1-{\beta }_2)g_{t,i}^2{V}_t=diag({\upsilon }_{t,1},{\upsilon }_{t,2},...,v_{t,d})\in R^{dd}$$ 但是这里要加上修正因子，即：（如果忘了这个回到前面去再看看指数加权移动平均值概念的最后部分） $$\hat{m}t=\frac{m_t}{1-{\beta }_1^t}\hat{v}t,i=\frac{v_{t,i}}{1-{\beta }_2^t}\hat{V}t=diag(\hat{v}t,1,\hat{v}t,2,...,\hat{v}t,d)\in R^{dd}$$ 所以，Adam的参数更新公式为： $$\Delta {\theta }_t=-\frac{\eta }{\sqrt{\hat{V}t+\epsilon }}\ast \hat{m}t{\theta }_{t+1}={\theta }_t-\frac{\eta }{\sqrt{\hat{V}t+\epsilon }}\ast \hat{m}t$$

1. 梯度消失和梯度爆炸
   

在分析梯度消失时，我们明白了导致其发生的主要原因是　$|\sigma {}^{\prime }(z_i)\ast w_i|\le \frac{1}{4}$ ，经链式法则反向传播后，越靠近输入层的参数的梯度越小。而导致梯度爆炸的原因是：$|\sigma {}^{\prime }(z_i)\ast w_i|>1$，当该表达式大于 1 时，经链式法则的指数倍传播后，前面层的参数的梯度会非常大，从而出现梯度爆炸。

但是要使得$|\sigma {}^{\prime }(z_i)w_i|>1$，就得 $|w_i|>4$才行，按照 $|\sigma {}^{\prime }(w_i{x}_i+b_i)\ast w_i|>1$，可以计算出 $x_i$ 的数值变化范围很窄，仅在公式(3)的范围内，才会出现梯度爆炸，因此梯度爆炸问题在使用 sigmoid 激活函数时出现的情况较少，不容易发生。

1. 卷积层和全连接层的区别
   卷积层相比于全连接层，主要有两个特点：

**局部连接：**全连接层是一种稠密连接方式，而卷积层却只使用卷积核对局部进行处理，这种处理方式其实也刚好对应了图像的特点。在视觉识别中，关键性的图像特征、边缘、角点等只占据了整张图像的一小部分，相隔很远的像素之间存在联系和影响的可能性是很低的，而局部像素具有很强的相关性。

**共享参数：**如果借鉴全连接层的话，对于1000×1000大小的彩色图像，一层全连接层便对应于三百万数量级维的特征，即会导致庞大的参数量，不仅计算繁重，还会导致过拟合。而卷积层中，卷积核会与局部图像相互作用，是一种稀疏连接，大大减少了网络的参数量。另外从直观上理解，依靠卷积核的滑动去提取图像中不同位置的相同模式也刚好符合图像的特点，不同的卷积核提取不同的特征，组合起来后便可以提取到高级特征用于最后的识别检测了。 所以 CNN 应用的条件一般是要求卷积对象有局部相关性，这正是图像所具备的，因此图像领域都是使用 CNN 就解释地通了。

1. 卷积运算量
   标准卷积层的FLOPs
   考虑bias：$(2\ast C_{int}\ast k^2)C_{out}HW$ 不考虑bias：$(2C_{int}\ast k^2-1)\ast C_{out}HW$

参数定义（下同）：$C_{int}$为输入通道数，k为卷积核边长， $C_{out}$为输出通道数，H*W为输出特征图的长宽。

其实卷积层在实现的时候可以选择加bias或者不加，在很多的框架当中是一个可以选择的参数，为了严谨，这里特地提一下。

怎么理解上面的公式呢？以不考虑bias为例。我们先计算输出的feature map中的一个pixel的计算量，然后再乘以feature map的规模大小即可，所以我们主要分析下上面公式中的括号部分： $$(2\ast C_{int}\ast k^2-1)=C_{int}\ast k^2+C_{int}\ast k^2-1$$

可以看到我们把它分成了两部分，第一项是乘法运算数，第二项是加法运算数，因为n个数相加，要加n-1次，所以不考虑bias，会有一个-1，如果考虑bias，刚好中和掉。

1. 为什么使用F1
   F1 score
   F1 score是分类问题中常用的评价指标，定义为精确率（Precision）和召回率（Recall）的调和平均数。 $$F1=\frac{1}{\frac{1}{Precision}+\frac{1}{Recall}}=\frac{2\times Precision\times Recall}{Precision+Recall}$$

补充一下精确率和召回率的公式：

TP（ True Positive）：真正例

FP（ False Positive）：假正例

FN（False Negative）：假反例

TN（True Negative）：真反例

精确率（Precision）: $Precision=\frac{TP}{TP+FP}$

召回率（Recall）: $Recall=\frac{TP}{TP+FN}$

精确率，也称为查准率，衡量的是预测结果为正例的样本中被正确分类的正例样本的比例。

召回率，也称为查全率，衡量的是真实情况下的所有正样本中被正确分类的正样本的比例。

F1 score 综合考虑了精确率和召回率，其结果更偏向于 Precision 和 Recall 中较小的那个，即 Precision 和 Recall 中较小的那个对 F1 score 的结果取决定性作用。例如若 $Precision=1,Recall\approx 0$，由F1 score的计算公式可以看出，此时其结果主要受 Recall 影响。

如果对 Precision 和 Recall 取算术平均值（$\frac{Precision+Recall}{2}$），对于 $Precision=1,Recall\approx 0$，其结果约为 0.5，而 F1 score 调和平均的结果约为 0。这也是为什么很多应用场景中会选择使用 F1 score 调和平均值而不是算术平均值的原因，因为我们希望这个结果可以更好地反映模型的性能好坏，而不是直接平均模糊化了 Precision 和 Recall 各自对模型的影响。