本文共 3317 字，大约阅读时间需要 11 分钟。

考试复盘

第一题？？是个什么互动哦，直接乱来的(￣￣)σ…(＿＿)ノ｜壁

第二题是前几天考过的，所以知道是$polya$，但是式子推到最后的二项式定理没推对，只能交暴力$FFT$，问题是暴力$FFT$都调了很久！！看来这一周还是得重点整一下卷积 [外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-pJWa65au-1616329681876)(file:///C:\PROGRA_{2\Baidu\BAIDUP}1\503900_{1.0\dict\Default\042396}1.PNG)]

第三题的期望，(・。・)突然想起自己还得抓紧整一下期望

已经算是简单的了，毕竟我一个对期望含义并不是很了解的人都找到了式子

但是卡在了后面的暴力找可挑点的时间复杂度上，而且这个好像还有点坑精度？？

LYK loves 消消看

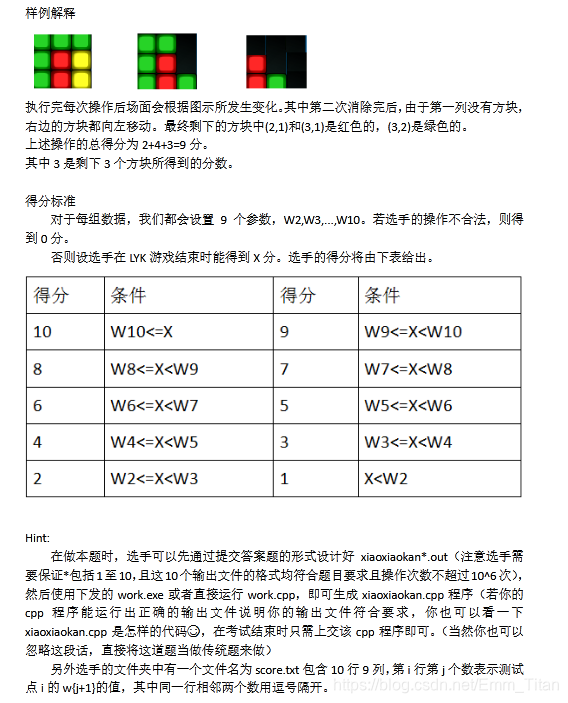
待补———————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————

LYK loves girls

$polya$定理，何老师简单解释了一下，染色种类数^轨道数/序列长度

#include <cstdio>#include <iostream>using namespace std;#define int long long#define mod 1000000007#define maxn 100005int n, k;int g[maxn], f[maxn], sum[maxn];int qkpow( int x, int y ) {   	int ans = 1;	while( y ) {   		if( y & 1 ) ans = ans * x % mod;		x = x * x % mod;		y >>= 1;	}	return ans;}int gcd( int x, int y ) {   	if( ! y ) return x;	else return gcd( y, x % y );}signed main() {   	scanf( "%lld %lld", &n, &k );	g[0] = g[1] = sum[0] = 1, sum[1] = 2;	for( int i = 2;i <= n;i ++ ) {   		g[i] = ( sum[i - 1] - ( ( i - k - 2 < 0 ) ? 0 : sum[i - k - 2] ) + mod ) % mod;		sum[i] = ( sum[i - 1] + g[i] ) % mod;	}	int ans = 0;	for( int i = 1;i <= n;i ++ ) {   		int d = gcd( n, i );		if( ! f[d] ) {   			for( int j = 1;j <= min( k + 1, d );j ++ ) 				f[d] = ( f[d] + j * g[d - j] % mod ) % mod;//1(m-j) 0 0 0 0 0 0 1(i) 			//乘以j就是因为最后面的0和1可以彼此旋转也是新的方案			if( k >= n ) f[d] = ( f[d] + 1 ) % mod;		}		ans = ( ans + f[d] ) % mod;	}	ans = ans * qkpow( n, mod - 2 ) % mod;	if( k == n ) ans = ( ans - 1 + mod ) % mod;	printf( "%lld\n", ans );	return 0;}

LYK loves jumping

$t_i\ne 0$，设能跳$x$个位置，期望步数和为$sum$，则$dp[i]=1+\frac{sum}{x}$
$t_i=0$，设能跳到$x$个$h$不等于$h_i$的位置，期望步数和为$sum$，$y$个$h$等于$h_i$的位置，则$dp[i]=\frac{x+y}{x}+\frac{sum}{x}$

#include <cstdio>#include <algorithm>using namespace std;#define maxn 100005struct node {   	int id, h, t;}dot[maxn];int n;bool vis[maxn];double step[maxn], sum[maxn], ans[maxn];bool cmp( node x, node y ) {   	return ( x.h == y.h ) ? x.t > y.t : x.h < y.h;}int main() {   	scanf( "%d", &n );	for( int i = 1;i <= n;i ++ ) scanf( "%d", &dot[i].h ), dot[i].id = i;	for( int i = 1;i <= n;i ++ ) scanf( "%d", &dot[i].t );	sort( dot + 1, dot + n + 1, cmp );	for( int i = 1;i <= n;i ++ ) {   		int l = 1, r = i;		while( l <= r ) {   			int mid = ( l + r ) >> 1;			if( dot[mid].h <= dot[i].h - dot[i].t ) l = mid + 1;			else r = mid - 1;		}		if( i == r ) {   //说明前i个格子都能跳 包括自己 那么意味着ti=0			int j;			for( j = i + 1;j <= n;j ++ )//i是特殊类型段的开头第一个 往后找于之等高切tj=0的格子				if( dot[j].h == dot[i].h && dot[j].t == dot[i].t );				else break;			j --;			for( int k = i;k <= j;k ++ ) {   				if( vis[k - 1] || i == 1 ) vis[k] = 1, step[k] = 0;				else step[k] = ( sum[i - 1] + j ) / ( i - 1 );				vis[k] |= vis[k - 1];				sum[k] = sum[k - 1] + step[k];			}			i = j;			continue;		}		if( vis[r] ) step[i] = 0;		else if( ! r ) step[i] = 1;		else step[i] = sum[r] / r + 1;		vis[i] |= vis[i - 1];		sum[i] = sum[i - 1] + step[i];	}	for( int i = 1;i <= n;i ++ ) ans[dot[i].id] = step[i];	for( int i = 1;i <= n;i ++ ) printf( "%.4f ", ans[i] );	return 0;}