
第二章 2.4 连续型随机变量及其概率密度


 解:
解: 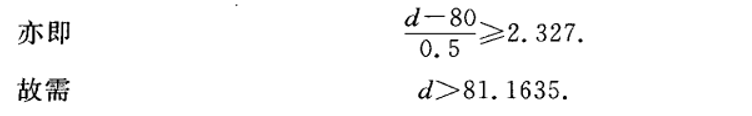
发布日期:2021-05-06 10:56:13
浏览次数:20
分类:精选文章
本文共 738 字,大约阅读时间需要 2 分钟。
2.4 连续型随机变量及其概率密度
文章目录
先来看在连续性随机变量中分布函数和概率密度函数的关系。


例 1:

解:


均匀分布
均匀分布顾名思义就是概率密度在某个区间内不变,如图:
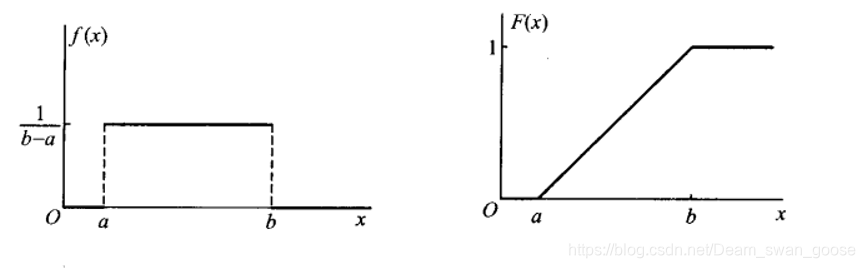


指数分布

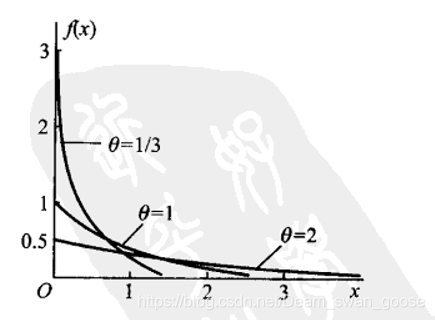
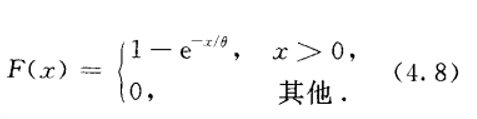
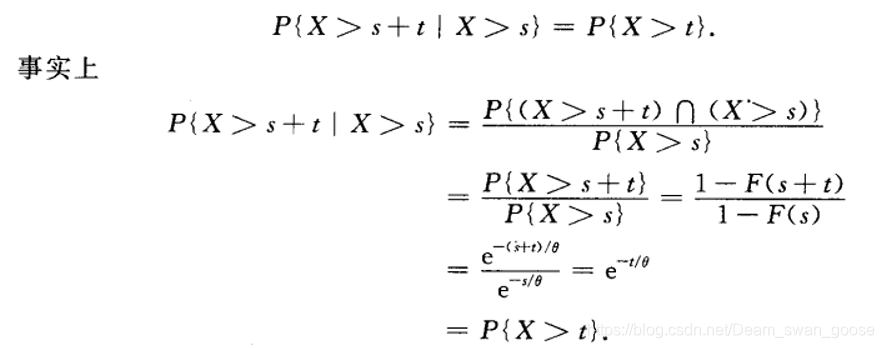
正态分布

性质:

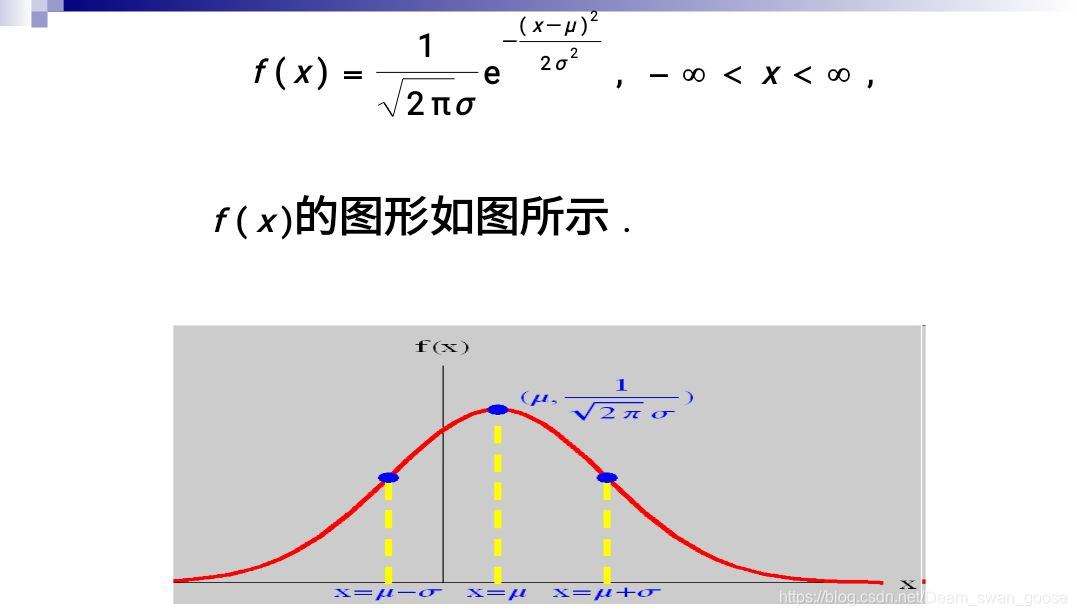
其中 μ \mu μ决定图形的左右位置, σ \sigma σ决定图形的高度。
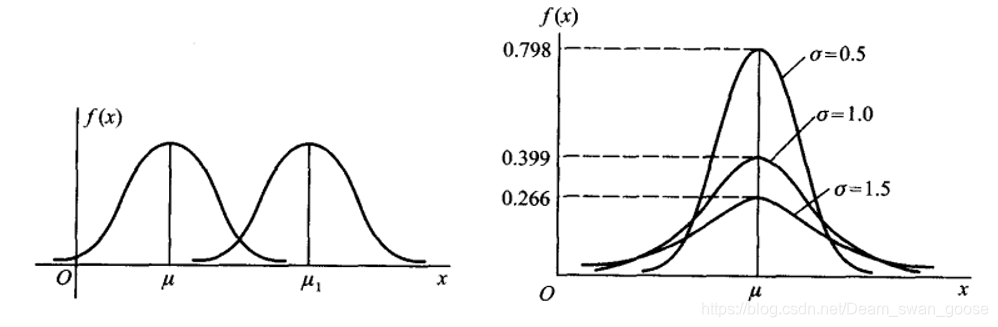



- 对于标准的正态分布来说 X X X的取值几乎都集中在[-3 , 3]之间。
- 对于一般的正态分布来说 X X X的取值几乎都集中在[ μ − 3 σ \mu - 3\sigma μ−3σ , μ + 3 σ \mu + 3\sigma μ+3σ]之间。(3 σ \sigma σ原则)
例:
 解:
解: 
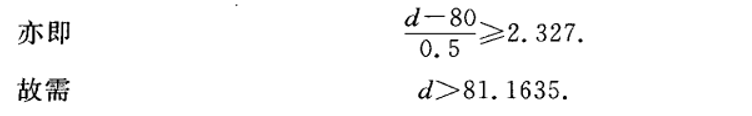
发表评论
最新留言
路过按个爪印,很不错,赞一个!
[***.219.124.196]2025年04月08日 00时58分39秒
关于作者

喝酒易醉,品茶养心,人生如梦,品茶悟道,何以解忧?唯有杜康!
-- 愿君每日到此一游!
推荐文章
C++中的delete加深认识
2019-03-06
windows消息机制(转)
2019-03-06
STL笔试面试题总结(干货)(转)
2019-03-06
XML 和 HTML 之间的差异
2019-03-06
阿里钉钉面试题
2019-03-06
华为社招笔试
2019-03-06
C++中找资源或者函数的方法
2019-03-06
一些留给自己的思考题(只求回过头来能够有所获)
2019-03-06
SQL函数返回表的写法
2019-03-06
delete对象时会自动调用类的析构函数
2019-03-06
C++ 子类对象直接赋值给父类对象可行,反过来不行
2019-03-06
linux下同一个动态库名为何辣么多的.so文件
2019-03-06
SQL联表的方式(逗号, Left Join, Right Join)
2019-03-06
牛客网输入输出举例
2019-03-06
字符串初始化时的注意点
2019-03-06
软考相关试题
2019-03-06
顺序表的操作
2019-03-06
常量表达式
2019-03-06
POD类型
2019-03-06
const与常量,傻傻分不清楚~
2019-03-06