第二章 2.5 随机变量的函数的分布
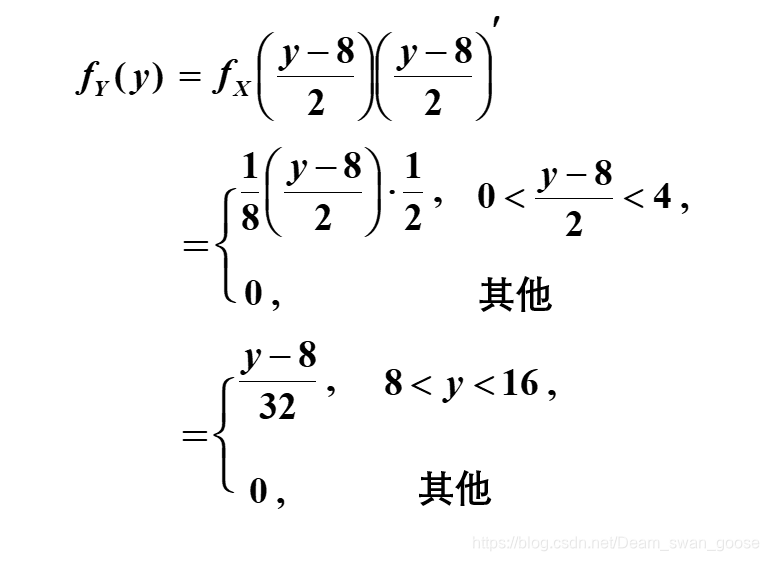
注意： 
注意： 这里因为 Y = X 2 Y = X^2 Y=X2 所以 Y Y Y肯定大于0.故我们把 ( 0 , − y ) (0, -\sqrt{y} ) (0,−y)这部分舍去。
发布日期：2021-05-06 10:56:14
浏览次数：23
分类：精选文章
本文共 532 字，大约阅读时间需要 1 分钟。
2.5 随机变量的函数的分布
文章目录
本小节讲的就是一个题型：已知随机变量 X X X的函数求含 X X X一维表达式的函数。
离散型随机变量的函数的分布
已知随机变量 X X X的分布律，求含 X X X一维表达式的分布律。
例：
连续型随机变量的函数的分布
已知随机变量 X X X的密度函数，求含 X X X一维表达式的密度函数。
思路：
求一维表达式的反函数（即写成 x x x = ……）然后把这个反函数当成一个整体去代替原式中的 x x x去求分布函数，再求导得到概率密度函数。
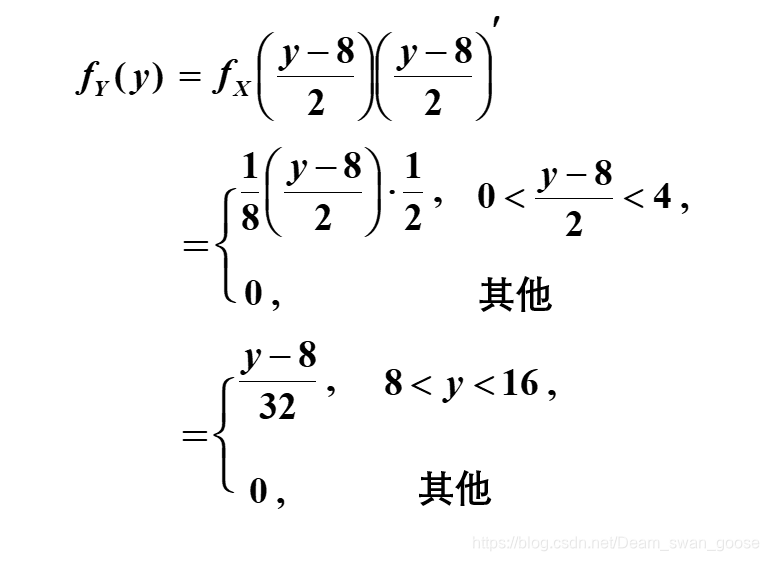
书上又提了一个公式法，那个思路和这个先求分布函数再求导其实是一样的。都是把那个反函数 h ( x ) h(x) h(x)整体代入然后求导（变上限积分函数要对上限求导）
公式法：
注意： - Y = g ( x ) Y = g(x) Y=g(x)中 g ( x ) g(x) g(x)要处处可导，且导数值要恒大于0或者恒小于0。
- 这个条件其实就是为了保证他可以用一个积分式子去表示。
例：
练：
注意： 这里因为 Y = X 2 Y = X^2 Y=X2 所以 Y Y Y肯定大于0.故我们把 ( 0 , − y ) (0, -\sqrt{y} ) (0,−y)这部分舍去。 发表评论
最新留言
路过按个爪印，很不错，赞一个！
[***.219.124.196]2025年03月19日 15时58分22秒
关于作者
喝酒易醉，品茶养心，人生如梦，品茶悟道，何以解忧？唯有杜康！
-- 愿君每日到此一游！
推荐文章
新生儿哭是因为什么
2019-03-05
nodeName与tagName的区别
2019-03-05
（九）实现页面底部购物车的样式
2019-03-05
在vue中给对象扩展属性的方法
2019-03-05
Neo4j : 通过节点的 id属性 对节点进行查，改，删操作
2019-03-05
【2021年新书推荐】ASP.NET Core 5 and Angular
2019-03-05
python-day3 for语句完整使用
2019-03-05
java基础知识：构造函数
2019-03-05
java基础知识：封装
2019-03-05
mysql 中的数据实现递归查询
2019-03-05
linux下远程上传命令scp
2019-03-05
（四）块设备文件
2019-03-05
可重入和不可重入函数
2019-03-05
（2.1）关系模型之关系结构和约束
2019-03-05
深入学习C++
2019-03-05
双系统基础上装三系统教程
2019-03-05
Android低级错误踩坑之Application
2019-03-05
android自定义无边框无标题的DialogFragment替代dialog
2019-03-05
白红宇的个人博客 - 记录点点滴滴的事 - 您是第 457444869 位访客