
7 优化算法






























发布日期:2021-06-29 18:40:43
浏览次数:2
分类:技术文章
本文共 4886 字,大约阅读时间需要 16 分钟。
文章目录
- 机器学习算法=模型表征+模型评估+优化算法。
- 优化算法就是
- 在模型表征空间中
- 找到模型评估指标
- 最好的模型。
- SVM对应的模型表征和评估指标分别为线性分类模型和最大间隔,
- 逻辑回归为线性分类模型和交叉熵
- 实际中多是大规模、高度非凸的优化
- 这给传统的基于全量数据、凸优化的优化理论带来挑战
- 优化虽古老,但大部分能用于训练深度神经网络的优化算法都是近几年提出,如Adam算法
1有监督学习的损失函数
场景描述
- 机器学习关键一环是模型评估
- 损失函数定义模型的评估指标。
- 没有损失函数就无法求解模型参数。
有监督涉及的损失函数?列举并简述特点
- 有监督学习中,损失函数刻画模型和训练样本的匹配程度。
- 训练样本为 ( x i , y i ) (x_i,y_i) (xi,yi)
- 参数为 θ \theta θ的模型可表示为函数

- 定义损失函数

- 越小,表明模型在该样本点匹配得越好
- 二分类
- Y = { 1 , − 1 } Y=\{1,-1\} Y={ 1,−1},
- 希望 s i g n ( f ( x i . θ ) ) = y i sign(f(x_i.\theta))=y_i sign(f(xi.θ))=yi,最自然的损失函数是0-1损失,

- 能刻画分类的错误率
- 非凸、非光滑,难直接对该函数优化。
- 0-1损失的一个代理是Hinge损失函数

- Hinge是0-1相对紧的凸上界
- 且当 f y ≥ 1 fy\ge 1 fy≥1时,不对其做任何惩罚。
- =1处不可导,不能用梯度下降法优化,
- 而用Subgradient Descent
- 0-1的另一个是 Logistic损失函数:
logistics损失函数原来和交叉熵不一样啊??

- 0-1的凸上界,处处光滑,可用梯度下降
- 该损失函数对所有的样本点都惩罚
- 因此对异常值更敏感
- 当预测值[-1,1]时,另一个常用是Cross Entropy

- 交叉熵也是0-1的光滑凸上界

- 对回归问题, Y = R Y=R Y=R,
- 希望 f ( x i , θ ) ≈ y i f(x_i,\theta)≈y_i f(xi,θ)≈yi
- 最常用是平方损失函数 L s q u r e ( f , y ) = ( f − y ) 2 (7.5) L_{squre}(f,y)=(f-y)^2\tag{7.5} Lsqure(f,y)=(f−y)2(7.5)
- 光滑函数,能用梯度下降法优化。
- 当预测值距离真实值越远时,惩罚力度越大
- 因此对异常点敏感。
- 为解决该问题,可用绝对损失函数
L a b s o l u t e = ∣ f − y ∣ (7.6) L_{absolute}=|f-y|\tag{7.6} Labsolute=∣f−y∣(7.6)
- 绝对损失函数相当于在做中值回归
- 相比做均值回归的平方损失函数
- 绝对损失函数对异常点更鲁棒
- 在 f = y f=y f=y处无法求导
- 综合可导性和对异常点的鲁棒性
- 可用Huber

- ∣ f − y ∣ |f-y| ∣f−y∣较小时为平方损失,较大时为线性
- 处处可导
- 对异常点鲁棒

- 损失函数还有很多,这里简单介绍几种常见
- 实际要针对特定问题和模型,选合适的损失函数,具体分析它的优缺点。
2 机器学习的优化问题
场景描述
- 大部分机器学习模型的参数估计都可写成优化问题
问题机器学习中的优化问题,哪些是凸优化问题,哪些非凸?
- 任意两点 x , y x,y x,y和任意实数 λ ∈ [ 0 , 1 ] \lambda\in[0,1] λ∈[0,1]总
L ( λ x + ( 1 − λ ) y ) ≤ λ L ( x ) + ( 1 − λ ) L ( ( y ) (7.8) L(\lambda x+(1-\lambda)y)\le \lambda L(x)+(1-\lambda)L((y)\tag{7.8} L(λx+(1−λ)y)≤λL(x)+(1−λ)L((y)(7.8)


- 二阶Hessian矩阵

上面是交叉熵吗?不是的!上面就是一个简单的线性分类吧!这本书上叫他logistics损失函数 !


-
主成分分析非凸
-
X = [ x 1 , . . . , x n ] X=[x_1,...,x_n] X=[x1,...,xn]为数据中心化后构成的矩阵

- X X X居然是个一列一列是样本!
- 我们不是习惯上是每行是一个样本的吗!
- 没关系,我也会做!
- V V V假设是 特 征 特征 特征维空间的 k k k个基! k k k个单位正交基!
- V V V是 k × 特 征 维 k \times 特征维 k×特征维矩阵!
- 这里涉及到了一个向量到一个向量空间的距离了吧!
- 我发出疑问:为啥那条平面就是一个向量空间呢!
efds
-
F 范数:对应元素的平方和再开方
-
证目标函数非凸
-
令 V ∗ V^* V∗为全局极小值,则 − V ∗ -V^* −V∗也是全局极小值
-
且

- 这不满足凸函数的定义
- 非凸难求解,但PCA是特例
- 可借助SVD直接得到主成分分析的全局极小
- 凸:支持向量机、线性回归等线性模型
- 非凸:低秩模型(如矩阵分解)、深度神经网络模型
3 经典优化算法
无约東优化问题的优化方法有哪些?
- 无约束优化

-
L ( ・ ) L(・) L(・)光滑
-
请问求解该问题的优化算法有哪些?适用场景是什么?
- 经典优化算法分直接法和迭代法
- 直接法要求目标函数需满足两条件。
- 第一个条件是,L(・)凸
- 最优解的充必要条件是梯度为0

- 第二个条件是,上式有闭式解。
- Ridge Regression

- 得到最优解为

- 迭代法就是迭代地修正对最优解的估计。
- 设当前对最优解的估计值为 θ t \theta_t θt,希望求解优化问题

- 来得到更好的估计值 θ t + 1 = θ t + δ t \theta_{t+1}=\theta_{t}+\delta_{t} θt+1=θt+δt
- 迭代法又可分一阶法和二阶法
- 一阶法对 L ( θ t + δ ) L(\theta_t+\delta) L(θt+δ)做一阶展开,得近似式

- 该近似式仅在 δ \delta δ较小时オ准确,
- 因此在求解,时一般加上 L 2 L_2 L2正则项

- 一阶法的迭代公式

-
α \alpha α称学习率
-
一阶法也称梯度下降法,梯度就是目标函数的一阶信息。
-
二阶法二阶泰勒展开,得近似式
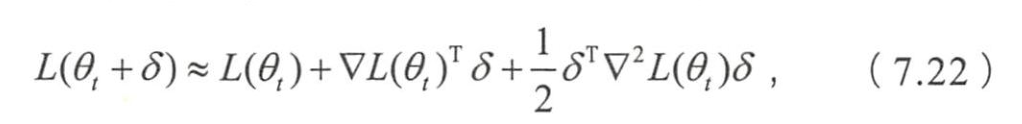
- Hessian矩阵。
- 求解近似优化问题
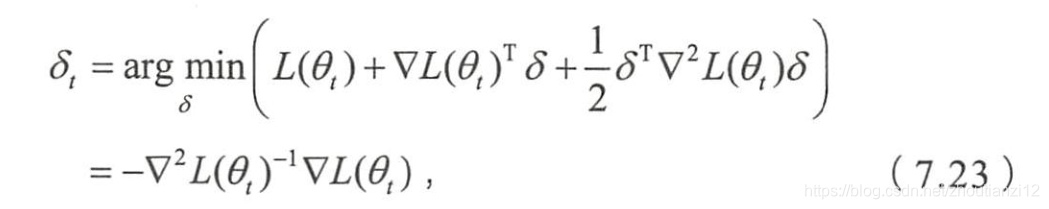
- 可得二阶法的迭代公式
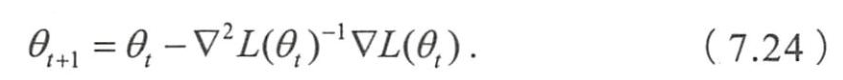
- 二阶法也称牛顿法,
- Hessian就是目标函数二阶信息
- 收敛速度一般远快一阶法,
- 但高维下, Hessian求逆的复杂度大
- 且当目标函数非凸时,
- 可能收敛到Saddle Point
- 俄数学家 Yurii Nesterov83提出一阶法的加速算法,
- 收敛速率能够达到一阶法收敛速率理论界
- 二阶法矩阵求逆的复杂度过高,
- Charles George Broyden,
- Roger Fletcher,
- Donald Goldfarb
- David Shanno 70年独立提出BFGS算法
- 89年扩展为低存储的L-BFGS算法。
- Charles George Broyden,
逸闻趣事
4梯度验证
场景描述
- 梯度下降法优化问题时,
- 最重要是计算目标函数的梯度
- 对复杂的
- 如深度神经网络,目标函数的梯度公式也复杂
- 易写错。
- 实际中,写出计算梯度的代码之后,
- 通常要验证自己写的代码是否正确。
如何验证求目标函数梯度功能的正确性?
hehhe
5随机梯度下降法
场景描述
- 梯度下降法,
- 每次迭代时需用所有训练数据
- 这给求解大规模数据的优化问题带来挑战
数据量特別大时,经典梯度下降法什么问题,如何改进?
- 优化问题的目标函数通常
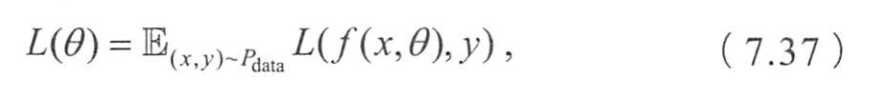
- θ \theta θ是待优化的模型参数
- x x x是模型输入
- 模型实际输出
- 模型的目标输出
- 刻画模型在数据(xy)上的损失
- 数据的分布
- 表示期望
- 刻画了当参数为 θ \theta θ时,模型在所有数据上的平均损失。
- 希望能找到平均损失最小的模型参数,
- 也就是求解

- 经典的梯度下降法用所有训练数据的平均损失来近似目标函数,
- 即
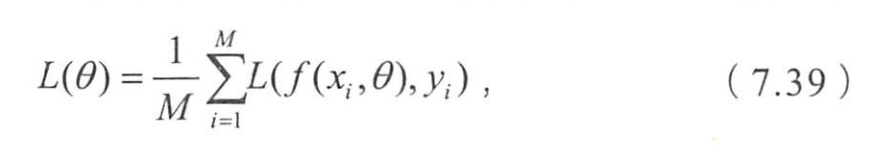
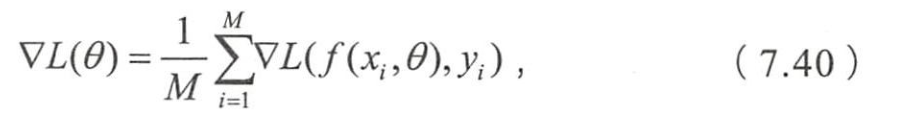
- M M M:训练样本的个数。
- 模型参数更新公式

- 经典的梯度下降法在每次对模型参数更新时,要遍历所有训练数据。
- SGD用单个训练样本的损失来近似平均损失,即

- SGD用单个训练数据即可对模型参数进行一次更新
- 大大加快收敛速率。
- 也适用于数据源源不断到来的在线更新场景。
- 为降低随机梯度的方差,使迭代算法更稳定,
- 为充分利用高度优化的矩阵运算操作,实际会同时处理若干训练数据
- (Mini- Batch Gradient Descent)。
- 同时处理m个

- 则目标函数及其梯度为

- 小批量梯度下降法
- (1)如何选m?
- 不同的应用中,最优m不一样,需通过调参选取。
- 2的幕能充分利用矩阵运算操作
- 可在2的幕次中挑选最优,如32、64、128、256
- (2)如何选m个训练数据?
- 一般每次遍历前,先对数据随机排序
- 然后每次迭代时按序挑m个数据直至遍历完所有数据
- (3)如何选学习速率a?
- 为加快收敛速率,同时提高求解精度
- 衰减学习速率的方案:一开始用大学习速率
- 误差曲线进入平台期后,减小学习速率做精细调整。
- 最优的学习速率方案也通常需要调参才能得到
- (Mini- Batch Gradient Descent)
- 每次更新模型参数时,只需处理m个训练数据即可,
- m<<M
- 这样能大大加快训练
- 每次更新模型参数时,只需处理m个训练数据即可,
7 L1正则化与稀疏性
场景描述
- 这道题能从细节入手,考察面试者对于机器学习模型各个相关环节的了解程度。
- 很多面试者能给出大概,深入且清晰并非易事。
- 下面从不同角度给出该问题的解答。
- 有些初学者会对问题存疑问
- 为什么希望模型参数有稀疏性?
- 就是模型的很多参数是0
- 为什么希望模型参数有稀疏性?
- 这相当于对模型进行一次特征选择
- 只留下ー些重要特征,提高模型的泛化能力,降低过拟合。
- 机器学习模型的输入动辄几百上干万维,
- 稀疏性就更重要,
- 谁也不希望把这上千万维的特征全部搬到线上
- 如果真这样
- 线上系统的同事会联合运维拿板砖找你
- 要在线上毫秒级的响应时间要求下完成干万维特征的提取以及模型的预测,还要在分布式环境下在内存中驻留那么大ー个模型,估计他们只能高呼“臣妾做不到啊”。
- 知道了面试官为什么要问这个问题后,下进入正题,
- 寻找L1正则化产生稀疏解的原因。
L1正则化使模型参数有稀疏性的原理是什么?
- 角度1:解空间形状
- 二维的情况,黄色是L2和L1正则项约東后的解空间,
- 绿色的等高线是凸优化中目标函数的等高线
- L2正则项约束后的解空间是圆形,
- L1约束的解空间是多边形。
- 多边形的解空可更容易在尖角处与等高线碰撞岀稀疏解

- 为什么加入正则项就是定义了ー个解空间约束?
- 为什么L1和L2的解空间是不同的?
- 可以通过KKT条件给出一种解释。
- “带正则项”和“带约束条件”等价。
- 为了约東 w w w的可能取值空间从而防止过拟合,我们为该最优化问题加上ー个约東,就是的L2范数的平方不能大于m:
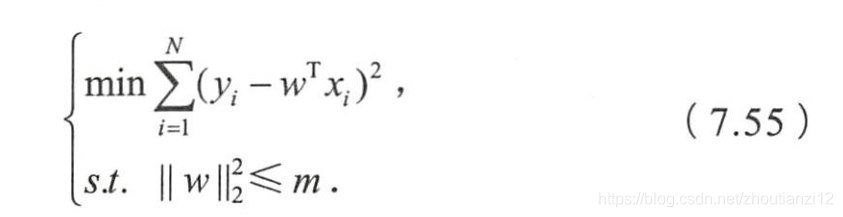
- 为求解带约束条件的凸优化问题,写出拉格朗日函数
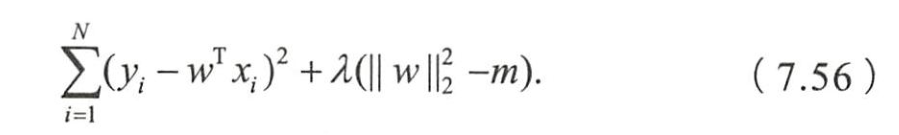
- 若 w ∗ w^* w∗和 λ ∗ \lambda^* λ∗是原问题和对偶问题的最优解,
- 则根据KKT条件,它门应满足
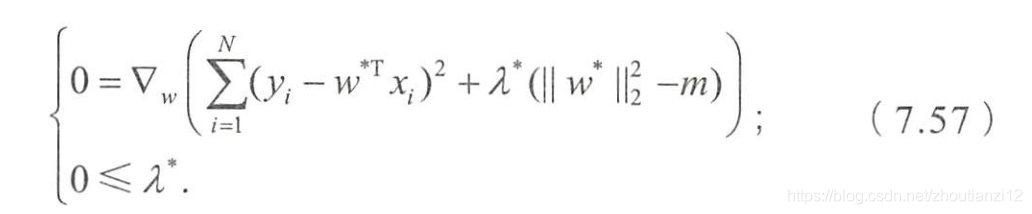
- 第一个式子不就是为带L2正则项的优化问题的最优解的条件嘛,
- λ \lambda λ就是L2正则顶前面的正则参数。
- L2相当于为参数定义了ー个圆形解空间,而L1相当于为参数定义了一个棱形的解空间。
- 如果原问题目标函数的最优解不是恰好落在解空间内,
- 那么约束条件下的最优解一定是在解空间的边界上,
- 而L1“棱角分明”的解空间显然更容易与目标函数等高线在角点碰撞,从而产生稀疏解。
- 第二个角度用更直观的图示来解释L1产生稀疏性这一现象。
- 仅考虑一维,多维类似,如图7.7
- 设棕线是原始目标函数 L ( w ) L(w) L(w)的曲线图,最小值点在蓝点处,且对应的 w ∗ w^* w∗非0

转载地址:https://cyj666.blog.csdn.net/article/details/104827317 如侵犯您的版权,请留言回复原文章的地址,我们会给您删除此文章,给您带来不便请您谅解!
发表评论
最新留言
路过,博主的博客真漂亮。。
[***.116.15.85]2024年04月29日 22时51分04秒
关于作者

喝酒易醉,品茶养心,人生如梦,品茶悟道,何以解忧?唯有杜康!
-- 愿君每日到此一游!
推荐文章
Koa2打怪升级之路:初识koa(一)
2019-04-30
日常随笔归纳总结:vue-router路由传参
2019-04-30
element-ui 的dialog增加水平拉伸、平移、放大、拖拽功能
2019-04-30
css cursor属性整理
2019-04-30
如何用element-ui的table做一个模糊搜索功能
2019-04-30
windows环境下,在node学习时使用nodemon 报错
2019-04-30
VScode自动生成项目目录文件结构的方法
2019-04-30
如何避免CSS :before、:after 中文乱码
2019-04-30
观察者模式
2019-04-30
1024. 视频拼接
2019-04-30
北漂码农的现状
2019-04-30
前端技巧必备:重置样式表reset.css
2019-04-30
css技巧--给选中的tab加下划线
2019-04-30
css技巧---位置中间的竖线|垂直居中
2019-04-30
css技巧---电子表体字体引入
2019-04-30
随笔---如何启动Redis
2019-04-30
css技巧---menu菜单加new
2019-04-30