本文共 2052 字，大约阅读时间需要 6 分钟。

梯度下降法——机器学习算法入门

在机器学习领域，找到最佳模型参数是一个关键步骤。线性回归模型的参数通常通过最小化代成本函数来确定，而梯度下降法是一种广泛应用的优化算法，帮助我们高效地找到最优解。本文将详细介绍梯度下降法的工作原理及其在单变量线性回归中的应用。

梯度下降法简述

梯度下降法（Gradient Descent）是一种无监督学习算法，通过不断调整模型参数来最小化代成本函数。它的核心思想是：在每次迭代中，按照参数的负梯度方向进行更新，逐步逼近最小化代成本的参数值。

在数学上，梯度下降法的更新规则可以表示为：

$$ θ = θ - α \cdot \nabla J(θ) $$

其中，θ是模型参数，α是步长常量，∇J(θ)是代成本函数关于θ的梯度。

梯度下降法的工作原理

为了直观理解梯度下降法的工作原理，我们可以考虑一个简单的线性回归模型。假设模型为：

$$ h(θ)(x) = θ_0 + θ_1 \cdot x $$

其中，θ₀和θ₁是需要确定的模型参数。代成本函数定义为：

$$ J(θ) = \frac{1}{2m} \sum_{i=1}^m (y_i - h(θ)(x_i))^2 $$

我们的目标是通过优化θ寻找最小的J(θ)。

1. 假设函数与代成本函数的几何意义

在几何上，代成本函数J(θ)表示的是预测值与真实值之间的误差平方的平均值。为了最小化这个值，我们需要找到最优的θ值。通过调整θ的值，可以看到代成本函数的形状。

例如，给定训练集 {(1,1), (2,2), (3,3)}，代成本函数的几何形状如下图所示：

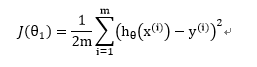
从图中可以看出，当θ₁=1时，代成本函数达到最小值。因此，最优的θ₁值为1。

2. 梯度下降法的迭代更新

梯度下降法通过以下步骤逐步优化θ的值：

3. 选取步长α的重要性

步长α是梯度下降法的重要超参数，直接影响优化过程的性能。具体表现为：

• α过大：可能导致参数跳过最优解，甚至进入无限循环。
• α过小：虽然能确保最终收敛，但效率极低，每次更新幅度过小。
• α适当：能够在有限步内达到较小的误差，并快速接近最优解。

因此，如何选择合适的α值是一个关键问题。通常，通过实验和交叉验证来确定最优的α值。

梯度下降法的数学推导

对于线性回归模型，梯度下降法的数学推导如下：

通过这些公式，我们可以看到梯度下降法是如何根据当前模型参数计算预测误差，并沿着误差方向相反的方向调整参数的。

梯度下降法的直观解释

在实际训练过程中，梯度下降法通过不断优化模型参数，使其逼近最优解。其核心思想是：

通过这样的迭代过程，代成本函数逐步减小，最终找到最小值。

梯度下降法的优缺点

尽管梯度下降法是一种简单有效的优化算法，但它也有一些局限性：

• 收敛速度：在某些情况下，如梯度较小时，收敛速度较慢。
• 参数依赖性：对初始参数的选择较敏感，可能导致收敛问题。
• 鞍点问题：有时候可能陷入代成本函数的鞍点而非最优解。

为了解决这些问题，后续算法如随机梯度下降法（SGD）和随机梯度下降法的变体（如小批量SGD）被提出了。

通过本文的介绍，可以看到梯度下降法的核心逻辑是通过迭代更新参数来最小化代成本函数。这种方法在机器学习中具有广泛的应用范围，尤其是在线性回归、分类和深度学习等领域。随着算法的不断改进，梯度下降法将继续在机器学习领域发挥重要作用。