CART
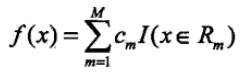易知每个单元Rm熵的固定输出值Cm最优值为样本在此单元上输出的均值。 在确定模型中采用了平方误差来进行误差确定 
j是特征j，s是特征j对应的一个取值（就是要确定怎样划分空间，用什么特征，特征中的那个值） 
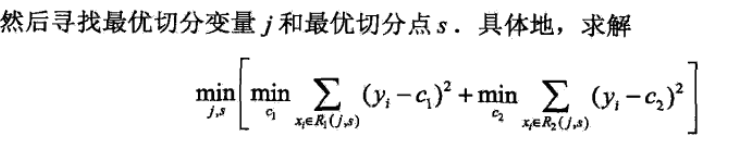[ ] 里面的就是二叉树的两部分，两部分最小化误差，那么根据求导可知: c1 = R1中y的均值，c2同理 
这样得到两个划分，再对这两个继续划分，最后得到回归树 回归树本质在于采用平方损失，找到划分的特征和取值 
就看G(D,A)哪个小选择哪个作为分类特征
发布日期：2021-05-09 14:26:28
浏览次数：19
分类：精选文章
本文共 384 字，大约阅读时间需要 1 分钟。
分为回归树和分类树
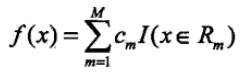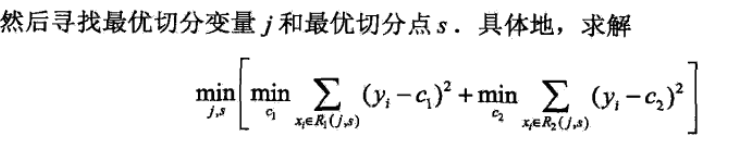CART前提是采用的二叉树决策树，不论是回归还是分类都是是/否 1。回归树 假设把输入空间划分，每个空间单元有一个固定的输出值，模型表示为： 易知每个单元Rm熵的固定输出值Cm最优值为样本在此单元上输出的均值。 在确定模型中采用了平方误差来进行误差确定 j是特征j，s是特征j对应的一个取值（就是要确定怎样划分空间，用什么特征，特征中的那个值） [ ] 里面的就是二叉树的两部分，两部分最小化误差，那么根据求导可知: c1 = R1中y的均值，c2同理 这样得到两个划分，再对这两个继续划分，最后得到回归树 回归树本质在于采用平方损失，找到划分的特征和取值 2。分类树
注意区别，这里由于是二叉树，对于特征取值多的，采用特征 = 1是不是这样的方式进行分叉 特征划分标准：基尼指数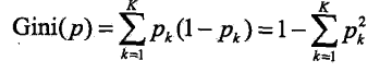
生成分类树的方法就是：
就看G(D,A)哪个小选择哪个作为分类特征 发表评论
最新留言
很好
[***.229.124.182]2025年04月19日 06时42分27秒
关于作者
喝酒易醉，品茶养心，人生如梦，品茶悟道，何以解忧？唯有杜康！
-- 愿君每日到此一游！
推荐文章
linux服务器系统的介绍----初学者
2021-05-11
2年经验大专生，拿下阿里有多难？（已拿offer，附上面经）
2021-05-11
从需求出发：QMUI 最新版 QMUISchemeHandler 的设计与实现解析
2021-05-11
浅谈持续集成(CI)、持续交付(CD)、持续部署(CD)
2021-05-11
成为一个优秀的测试工程师需要具备哪些知识和经验？
2021-05-11
深入理解SQL的四种连接-左外连接、右外连接、内连接、全连接
2021-05-11
HDU4814——数学，模拟进制转换
2021-05-11
LeetCode LCP 3 机器人大冒险
2021-05-11
Cisco网络模拟器踩坑记录
2021-05-11
LeetCode 947. 移除最多的同行或同列石头 并查集
2021-05-11
一些JavaSE学习过程中的思路整理(二)（主观性强，持续更新中...）
2021-05-11
JavaScript中如何给按钮设置隐藏与显示属性
2021-05-11
CSS——NO.4(继承、层叠、特殊性、重要性)
2021-05-11
Python——11面向对象编程基础
2021-05-11
Python——5函数
2021-05-11
C++中如何对单向链表操作
2021-05-11
C++走向远洋——63（项目二2、两个成员的类模板）
2021-05-11
6——PHP顺序结构&&字符串连接符
2021-05-11
C++扬帆远航——2
2021-05-11
C++扬帆远航——1
2021-05-11
白红宇的个人博客 - 记录点点滴滴的事 - 您是第 460896947 位访客
访问时间: 2025-04-30 11:16:03
访问IP: 18.221.113.108
Copyright © 2020 - 2025 css8.cn 京ICP备2021015314号-1
手机版