
【花书笔记】第2章 线性代数
 元素对应乘积(Hadamard乘积):两个矩阵的标准乘积不是指两个矩阵中对应元素的乘积。不过,那样的矩阵操作确实是存在的,被称为元素对应乘积(element-wise product)或者Hadamard 乘积(Hadamard product),记为 A ⊙ B。 点积:两个相同维数的向量 x 和 y 的点积(dot product)可看作是矩阵乘积 x ⊤ y。
元素对应乘积(Hadamard乘积):两个矩阵的标准乘积不是指两个矩阵中对应元素的乘积。不过,那样的矩阵操作确实是存在的,被称为元素对应乘积(element-wise product)或者Hadamard 乘积(Hadamard product),记为 A ⊙ B。 点积:两个相同维数的向量 x 和 y 的点积(dot product)可看作是矩阵乘积 x ⊤ y。 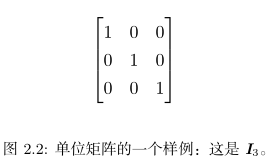 逆矩阵:
逆矩阵: 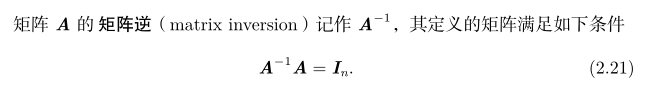
 3.p=2时,L²范数是欧几里得范数,表示从原点出发到向量x确定的点的欧几里得距离。 4.平方L²范数也经常用来衡量向量的大小,可以简单的通过点积
3.p=2时,L²范数是欧几里得范数,表示从原点出发到向量x确定的点的欧几里得距离。 4.平方L²范数也经常用来衡量向量的大小,可以简单的通过点积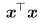 计算。 5.平方L²范数在计算上比L²范数本身方便,但是它在原点附近增长得十分缓慢。在某些机器学习应用中,区分恰好是零的元素和非零但值很小的元素是很重要的。 6.L¹范数:
计算。 5.平方L²范数在计算上比L²范数本身方便,但是它在原点附近增长得十分缓慢。在某些机器学习应用中,区分恰好是零的元素和非零但值很小的元素是很重要的。 6.L¹范数: 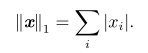 7.Lº范数(这个术语只是一些坐着自己叫的):统计向量中非零元素的个数来衡量向量的大小。 8.最大范数:
7.Lº范数(这个术语只是一些坐着自己叫的):统计向量中非零元素的个数来衡量向量的大小。 8.最大范数:  9.Frobenius范数:
9.Frobenius范数:  10.两个向量的点积
10.两个向量的点积 
 3.单位向量
3.单位向量  4.标准正交
4.标准正交  5.正交矩阵
5.正交矩阵 
 3.
3. 4.
4. 5.
5.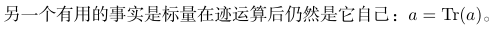
发布日期:2021-05-08 14:22:37
浏览次数:25
分类:精选文章
本文共 1303 字,大约阅读时间需要 4 分钟。
2.1 标量、向量、矩阵和张量
标量:一个单独的数。
向量:一列数。 矩阵:一个二维数组。 张量:一个数组中的元素分布在若干维坐标的规则网络中,我们称之为张量。 转置:矩阵的转置是以对角线为轴的镜像。2.2 矩阵和向量相乘
矩阵乘积:
 元素对应乘积(Hadamard乘积):两个矩阵的标准乘积不是指两个矩阵中对应元素的乘积。不过,那样的矩阵操作确实是存在的,被称为元素对应乘积(element-wise product)或者Hadamard 乘积(Hadamard product),记为 A ⊙ B。 点积:两个相同维数的向量 x 和 y 的点积(dot product)可看作是矩阵乘积 x ⊤ y。
元素对应乘积(Hadamard乘积):两个矩阵的标准乘积不是指两个矩阵中对应元素的乘积。不过,那样的矩阵操作确实是存在的,被称为元素对应乘积(element-wise product)或者Hadamard 乘积(Hadamard product),记为 A ⊙ B。 点积:两个相同维数的向量 x 和 y 的点积(dot product)可看作是矩阵乘积 x ⊤ y。 2.3 单位矩阵和逆矩阵
单位矩阵:
 逆矩阵:
逆矩阵: 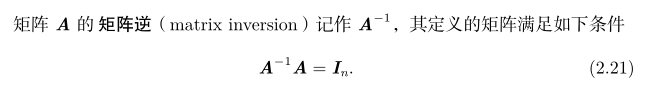
2.4 线性相关和生成子空间
线性相关:
线性无关:如果一组向量中的任意一个向量都不能表示成其他向量的线性组合,那么这组向量称为线性无关。2.5 范数
1.
 3.p=2时,L²范数是欧几里得范数,表示从原点出发到向量x确定的点的欧几里得距离。 4.平方L²范数也经常用来衡量向量的大小,可以简单的通过点积
3.p=2时,L²范数是欧几里得范数,表示从原点出发到向量x确定的点的欧几里得距离。 4.平方L²范数也经常用来衡量向量的大小,可以简单的通过点积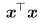 计算。 5.平方L²范数在计算上比L²范数本身方便,但是它在原点附近增长得十分缓慢。在某些机器学习应用中,区分恰好是零的元素和非零但值很小的元素是很重要的。 6.L¹范数:
计算。 5.平方L²范数在计算上比L²范数本身方便,但是它在原点附近增长得十分缓慢。在某些机器学习应用中,区分恰好是零的元素和非零但值很小的元素是很重要的。 6.L¹范数: 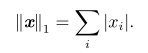 7.Lº范数(这个术语只是一些坐着自己叫的):统计向量中非零元素的个数来衡量向量的大小。 8.最大范数:
7.Lº范数(这个术语只是一些坐着自己叫的):统计向量中非零元素的个数来衡量向量的大小。 8.最大范数:  9.Frobenius范数:
9.Frobenius范数:  10.两个向量的点积
10.两个向量的点积 
2.6 特殊类型的矩阵和向量
1.对角矩阵
2.对称矩阵 3.单位向量
3.单位向量  4.标准正交
4.标准正交  5.正交矩阵
5.正交矩阵 
2.7 特征分解
1.
2.8 奇异值分解
1.
2.9 Moore-Penrose伪逆

2.10 迹运算
1.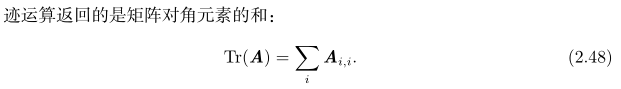
 3.
3. 4.
4. 5.
5.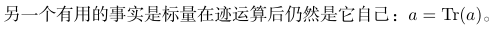
2.11 行列式
行列式,记作 det(A),是一个将方阵 A 映射到实数的函数。行列式等于矩阵特征值的乘积。行列式的绝对值可以用来衡量矩阵参与矩阵乘法后空间扩大或者缩小了多少。如果行列式是 0,那么空间至少沿着某一维完全收缩了,使其失去了所有的体积。如果行列式是 1,那么这个转换保持空间体积不变。
2.12 主成分分析(PCA)
发表评论
最新留言
表示我来过!
[***.240.166.169]2025年03月28日 06时48分13秒
关于作者

喝酒易醉,品茶养心,人生如梦,品茶悟道,何以解忧?唯有杜康!
-- 愿君每日到此一游!
推荐文章
VUE3(八)setup与ref函数
2021-05-08
智能合约开发实践(1)
2021-05-08
CMake自学记录,看完保证你知道CMake怎么玩!!!
2021-05-08
ORB-SLAM2:LoopClosing线程学习随笔【李哈哈:看看总有收获篇】
2021-05-08
MySQL隐藏文件.mysql_history风险
2021-05-08
js求阶乘
2021-05-08
L1-009 N个数求和 (20 分)
2021-05-08
L2-031 深入虎穴 (25 分)
2021-05-08
简单的xml读取存储方法(未优化)
2021-05-08
Nginx---惊群
2021-05-08
2种解法 - 获取一条直线上最多的点数
2021-05-08
项目中常用的审计类型概述
2021-05-08
(九)实现页面底部购物车的样式
2021-05-08
python-day3 for语句完整使用
2021-05-08
ButterKnife使用问题
2021-05-08
为什么讨厌所谓仿生AI的说法
2021-05-08
ORACLE 客户端工具
2021-05-08
Pyinstaller打包的exe文件过大的解决方法
2021-05-08