本文共 5490 字，大约阅读时间需要 18 分钟。

1053 Path of Equal Weight （30 分）

Given a non-empty tree with root R, and with weight W​i​​ assigned to each tree node T​i​​. The weight of a path from R to L is defined to be the sum of the weights of all the nodes along the path from R to any leaf node L.

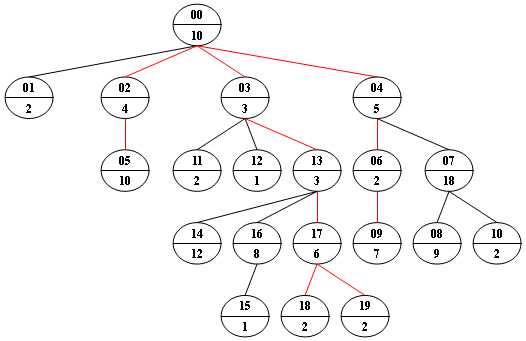
Now given any weighted tree, you are supposed to find all the paths with their weights equal to a given number. For example, let's consider the tree showed in the following figure: for each node, the upper number is the node ID which is a two-digit number, and the lower number is the weight of that node. Suppose that the given number is 24, then there exists 4 different paths which have the same given weight: {10 5 2 7}, {10 4 10}, {10 3 3 6 2} and {10 3 3 6 2}, which correspond to the red edges in the figure.

Input Specification:

Each input file contains one test case. Each case starts with a line containing 0<N≤100, the number of nodes in a tree, M (<N), the number of non-leaf nodes, and 0<S<2​30​​, the given weight number. The next line contains N positive numbers where W​i​​ (<1000) corresponds to the tree node T​i​​. Then M lines follow, each in the format:

ID K ID[1] ID[2] ... ID[K]

where ID is a two-digit number representing a given non-leaf node, K is the number of its children, followed by a sequence of two-digit ID's of its children. For the sake of simplicity, let us fix the root ID to be 00.

Output Specification:

For each test case, print all the paths with weight S in non-increasing order. Each path occupies a line with printed weights from the root to the leaf in order. All the numbers must be separated by a space with no extra space at the end of the line.

Note: sequence {A​1​​,A​2​​,⋯,A​n​​} is said to be greater than sequence {B​1​​,B​2​​,⋯,B​m​​} if there exists 1≤k<min{n,m} such that A​i​​=B​i​​ for i=1,⋯,k, and A​k+1​​>B​k+1​​.

Sample Input:

20 9 2410 2 4 3 5 10 2 18 9 7 2 2 1 3 12 1 8 6 2 200 4 01 02 03 0402 1 0504 2 06 0703 3 11 12 1306 1 0907 2 08 1016 1 1513 3 14 16 1717 2 18 19

Sample Output:

10 5 2 710 4 1010 3 3 6 210 3 3 6 2

一， 我的代码（第一个形参为待检测结点，麻烦）

#include
   
    #include
    
     #include
     
      #include
      
       using namespace std;const int max_n = 110;int N = 0, M = 0, S = 0;int times = 0;struct Node {	int weight;	int layer;	vector
       
         child;}node[max_n];vector
        
          temp;vector
         
           ans[max_n];bool cmp(int a, int b) { return node[a].weight > node[b].weight;}/*void insert_layer(int root) { node[root].layer = 1; queue
          
            que; que.push(root); while (!que.empty()) { int top = que.front(); que.pop(); for (int i = 0; i < node[top].child.size(); i++) { node[node[top].child[i]].layer = node[top].layer + 1; } }}*/void DFS(int root, int nowSum) { if (nowSum + node[root].weight == S&&node[root].child.size() == 0) { temp.push_back(node[root].weight); ans[times++] = temp; temp.pop_back(); return; } if (nowSum + node[root].weight >= S)return; temp.push_back(node[root].weight); for (int i = 0; i < node[root].child.size(); i++) { DFS(node[root].child[i], nowSum + node[root].weight); } temp.pop_back();}int main() { int single_weight = 0;; scanf("%d %d %d", &N, &M, &S); for (int i = 0; i < N; i++) { scanf("%d", &single_weight); node[i].weight = single_weight; } for (int i = 0; i < M; i++) { int no_leaf_id = 0, num = 0, node_id = 0; scanf("%d %d", &no_leaf_id, &num); for (int j = 0; j < num; j++) { scanf("%d", &node_id); node[no_leaf_id].child.push_back(node_id); } sort(node[no_leaf_id].child.begin(), node[no_leaf_id].child.end(), cmp); }// node[0].layer = 1;// insert_layer(0); DFS(0, 0); for (int i = 0; i < times; i++) { for (int j = 0; j < ans[i].size(); j++) { printf("%d", ans[i][j]); if (j != ans[i].size() - 1) { printf(" "); } } printf("\n"); } return 0;}
          
         
        
       
      
     
    
   

二， 标准代码（第一个形参为已添加进有效结点的结点）

#include
   
    #include
    
     #include
     
      #include
      
       using namespace std;const int max_n = 110;int N = 0, M = 0, S = 0;int times = 0;struct Node {	int weight;	int layer;	vector
       
         child;}node[max_n];vector
        
          temp;vector
         
           ans[max_n];bool cmp(int a, int b) { return node[a].weight > node[b].weight;}/*void insert_layer(int root) { node[root].layer = 1; queue
          
            que; que.push(root); while (!que.empty()) { int top = que.front(); que.pop(); for (int i = 0; i < node[top].child.size(); i++) { node[node[top].child[i]].layer = node[top].layer + 1; } }}*/void DFS(int root, int nowSum) { if (nowSum > S)return; if (nowSum == S) { if (node[root].child.size() != 0)return; else { ans[times++] = temp; } } for (int i = 0; i < node[root].child.size(); i++) { int child = node[root].child[i]; temp.push_back(node[child].weight); DFS(child, nowSum + node[node[root].child[i]].weight); temp.pop_back(); }}int main() { int single_weight = 0;; scanf("%d %d %d", &N, &M, &S); for (int i = 0; i < N; i++) { scanf("%d", &single_weight); node[i].weight = single_weight; } for (int i = 0; i < M; i++) { int no_leaf_id = 0, num = 0, node_id = 0; scanf("%d %d", &no_leaf_id, &num); for (int j = 0; j < num; j++) { scanf("%d", &node_id); node[no_leaf_id].child.push_back(node_id); } sort(node[no_leaf_id].child.begin(), node[no_leaf_id].child.end(), cmp); }// node[0].layer = 1;// insert_layer(0); temp.push_back(node[0].weight); DFS(0, node[0].weight); for (int i = 0; i < times; i++) { for (int j = 0; j < ans[i].size(); j++) { printf("%d", ans[i][j]); if (j != ans[i].size() - 1) { printf(" "); } } printf("\n"); } return 0;}