本文共 4482 字，大约阅读时间需要 14 分钟。

前言

本文讲述快速幂的原理，以及用法

一、快速幂（Fast Exponentiation）的定义：

定义：快速求，取base为底数的exp次幂，即求：base^exp；

时间复杂度： O(log₂N)

二、快速幂原理：

思想：每一步都把指数分成两半，而相应的底数做平方运算。不仅能把非常大的指数给不断变小，所需要执行的循环次数也变小，而最后表示的结果却一直不会变。

原理：(a* b) % m = ((a % m) * (b % m)) % m

三、常规求幂：

代码块：

#include <bits/stdc++.h>using namespace std;typedef long long ll;ll Pow1(ll my_base, ll my_exp) {
   	ll ans = 1;	for (int i = 1; i <= my_exp; i++) ans *= my_base;	return ans;}int main() {
   	ios::sync_with_stdio(false);	cin.tie(0); //断开同步流 	ll my_base, my_exp, result;	clock_t my_start, my_end;	cin >> my_base >> my_exp;	my_start = clock();	//该函数返回值是硬件滴答数	result = Pow1(my_base, my_exp);	cout << my_base << "^" << my_exp << "=" << result << endl;	my_end = clock();	cout << "time=" << ((double)my_end - my_start) / CLK_TCK << "s" << endl;	//要换算成秒，需要除以CLK_TCK或者 CLK_TCKCLOCKS_PER_SEC	return 0;}

运行结果：

四、简单快速求幂：

代码块：

#include <bits/stdc++.h>using namespace std;typedef long long ll;ll Pow2(ll x, ll y) {
   	ll ans = 1, base = x;	while (y != 0) {
   		if (y % 2 != 0) ans *= base;		base *= base;		y /= 2;	}	return ans;}int main() {
   	ios::sync_with_stdio(false);	cin.tie(0); //断开同步流 	ll my_base, my_exp, result;	clock_t my_start, my_end;	cin >> my_base >> my_exp;	my_start = clock();	//该函数返回值是硬件滴答数	result = Pow2(my_base, my_exp);	cout << my_base << "^" << my_exp << "=" << result << endl;	my_end = clock();	cout << "time=" << ((double)my_end - my_start) / CLK_TCK << "s" << endl;	//要换算成秒，需要除以CLK_TCK或者 CLK_TCKCLOCKS_PER_SEC	return 0;}

运行结果：

四、递归快速求幂：

代码块：

#include <bits/stdc++.h>using namespace std;typedef long long ll;ll Pow3(ll my_base, ll my_exp) {
   	if (my_exp == 1)return my_base;	ll ans = Pow3(my_base, my_exp / 2);	return (my_exp % 2 == 0 ? 1 : my_base) * ans * ans;}int main() {
   	ios::sync_with_stdio(false);	cin.tie(0); //断开同步流 	ll my_base, my_exp, result;	clock_t my_start, my_end;	cin >> my_base >> my_exp;	my_start = clock();	//该函数返回值是硬件滴答数	result = Pow3(my_base, my_exp);	cout << my_base << "^" << my_exp << "=" << result << endl;	my_end = clock();	cout << "time=" << ((double)my_end - my_start) / CLK_TCK << "s" << endl;	//要换算成秒，需要除以CLK_TCK或者 CLK_TCKCLOCKS_PER_SEC	return 0;}

运行结果：

五、位运算快速求幂：

代码块：

#include <bits/stdc++.h>using namespace std;typedef long long ll;ll Pow3(ll my_base, ll my_exp) {
   	int ans = 1, base = my_base;	while (my_exp != 0) {
   		if (my_exp & 1 != 0)		{
   			//逐位获取b的二进制位，遇0累乘			ans *= base;		}		base *= base;		my_exp >>= 1;	}	return ans;}int main() {
   	ios::sync_with_stdio(false);	cin.tie(0); //断开同步流 	ll my_base, my_exp, result;	clock_t my_start, my_end;	cin >> my_base >> my_exp;	my_start = clock();	//该函数返回值是硬件滴答数	result = Pow3(my_base, my_exp);	cout << my_base << "^" << my_exp << "=" << result << endl;	my_end = clock();	cout << "time=" << ((double)my_end - my_start) / CLK_TCK << "s" << endl;	//要换算成秒，需要除以CLK_TCK或者 CLK_TCKCLOCKS_PER_SEC	return 0;}

运行结果：

六、高精度快速求幂：

代码块：

#include <bits/stdc++.h>using namespace std;typedef long long ll;const ll mod = 1e7;   //自定义取模的数据,视数据大小的情况而定//a ^ bll ksm(ll a, ll b, ll mod) {
       //time_complex=O(logn)	ll ans = 1, base = a;	while (b != 0) {
   		if ((b & 1) != 0) {
      //“b & 1”指取b的二进制数的最末位			ans = (ans * base) % mod;   //累乘，以便随时对ans做出贡献。		}		base = (base * base) % mod;		b >>= 1;    //右移1位，删去最低位。	}	return ans;}int main() {
   	ios::sync_with_stdio(false);	cin.tie(0); //断开同步流 	ll a, b, result;	clock_t my_start, my_end;	cin >> a >> b;	my_start = clock();	//该函数返回值是硬件滴答数	result = ksm(a, b, mod); 	cout << a << "^" << b << "=" << result << endl;	my_end = clock();	cout << "time=" << ((double)my_end - my_start) / CLK_TCK << "s" << endl;	//要换算成秒，需要除以CLK_TCK或者 CLK_TCKCLOCKS_PER_SEC	return 0;}

运行结果：

六、python高精度快速求幂：

代码块：

a, b = map(int, input().split())mod = 10000000result = pow(a, b, mod)print("{0}^{1}={2}".format(a, b, result))

运行结果：

七、实战演习：

题目来源：

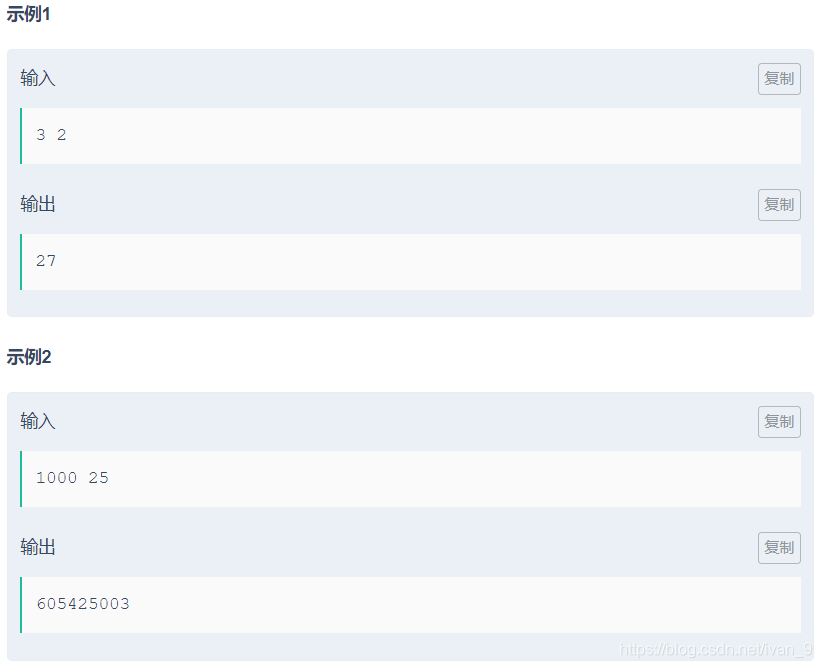
程序代码：
第一种写法：

#include<bits/stdc++.h>using namespace std;typedef long long ll;/*long long qmod(ll a,ll b,int c){    if(b==1) return a;    if(b&1) return a*qmod(a,b-1,c)%c;    else    {        ll m=qmod(a,b/2,c);        return m*m%c;    }    } *///用二分还是超时ll qmod(ll a,ll b,ll c)//快速幂{
       int r=1;    while(b)    {
           if(b&1) r=a*r%c;        a=a*a%c;        b>>=1; //b的二进制形式删除最后一位    }    return r;}int main(){
       long long a,b,c;    c=998244353;    cin>>a>>b;    if(a>c) a=a%c;    else    {
           ll ans=qmod(b+1,a,c);        cout<<ans<<endl;    }        }

第二种写法：

n, m = map(int, input().split())sum = pow(m+1,n,998244353)print(sum)

运行结果：

总结

本文讲述快速幂的基本用法。

如有错误，敬请指教！