本文共 1821 字，大约阅读时间需要 6 分钟。

分析

给出两个字符A和B，求A和B最长公共子序列长度以及最长的长度个数有几个。

###1. 首先求最长公共子序列
最长公共子序列问题：

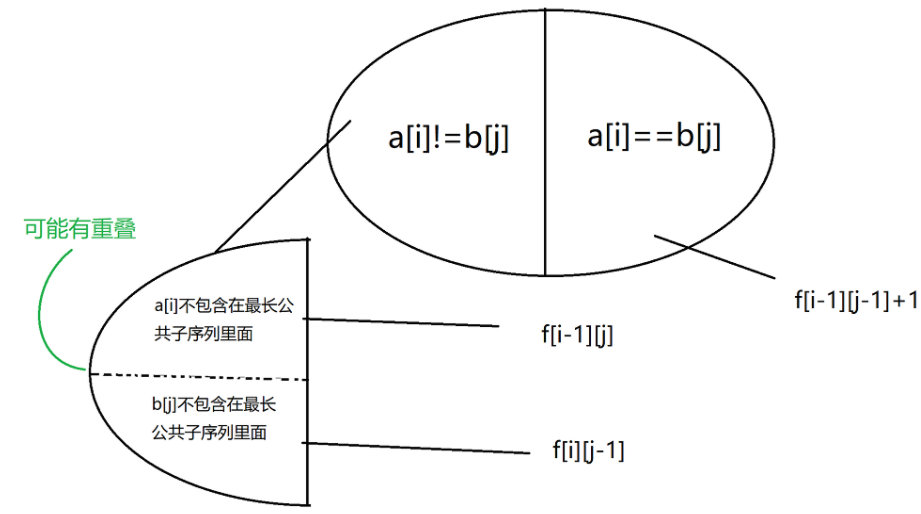
###2. 求出了最长的长度，之后要同时把长度的数目计算清楚。
用cnt[i][j]表示A前i位，B前j位的最长公共子序列数目。
对于每个f[i][j]:
1. 若f[i][j]==f[i-1][j],说明状态是从f[i-1][j]转移来的，cnt[i][j]要加上cnt[i-1][j]
2. 若f[i][j]==f[i][j-1],说明状态是从f[i][j-1]转移来的，cnt[i][j]要加上cnt[i][j-1]
3. 若a[i]==b[j]且f[i][j]==f[i-1][j-1]+1,说明状态是从f[i-1][j-1]转移来的，cnt[i][j]要加上cnt[i-1][j-1]
4. 若a[i]!=b[j]且f[i][j]==f[i-1][j-1],那么状态cnt[i-1][j-1]会多加上一次，所以要让cnt[i][j]-=cnt[i-1][j-1]

C++ 代码

#include<bits/stdc++.h>using namespace std;const int N = 5010,mod = 1e8;int f[2][N],cnt[2][N];  //为防止内存溢出MLE，使用滚动数组，因为每个状态只与上一个状态有关char s[N],t[N];int main(){    scanf("%s%s",s+1,t+1);    int n=strlen(s+1)-1,m=strlen(t+1)-1;    for(int i=0;i<=m;i++)   //初始化，长度为0最长子序列方案数为1（第一个序列长度为0）         cnt[0][i]=1;    cnt[1][0]=1;    //初始化，长度为0最长子序列方案数为1（第二个序列长度为0）         for(int i=1;i<=n;i++)    {        int now=i&1,pre=now^1;  //当前状态为now,前一个状态为pre        for(int j=1;j<=m;j++)        {            f[now][j]=max(f[pre][j],f[now][j-1]);   //最长公共子序列前两种情况            cnt[now][j]=0;            if(s[i]==t[j])              {                f[now][j]=max(f[now][j],f[pre][j-1]+1); //最长公共子序列第三种种情况                if(f[now][j]==f[pre][j-1]+1) cnt[now][j]=cnt[pre][j-1];     //如果此时满足当前序列f[now][j]等于上一序列f[pre][j-1]+1，cnt当前状态则从上一个状态转移过来            }            else            {                if(f[now][j]==f[pre][j-1]) cnt[now][j]-=cnt[pre][j-1];  //s[i]!=t[j]并且满足当前序列f[now][j]等于上一序列f[pre][j-1],cnt要减去上一状态的数目，防止重复            }            if(f[now][j]==f[pre][j]) cnt[now][j]=(cnt[now][j]+cnt[pre][j])%mod; //状态是从f[i-1][j]转移来的，cnt[i][j]要加上cnt[i-1][j]            if(f[now][j]==f[now][j-1]) cnt[now][j]=(cnt[now][j]+cnt[now][j-1])%mod; //状态是从f[i][j-1]转移来的，cnt[i][j]要加上cnt[i][j-1]                }    }    printf("%d\n",f[n&1][m]);       printf("%d\n",cnt[n&1][m]);    return 0;}