本文共 1877 字，大约阅读时间需要 6 分钟。

1、定义

叶子结点的权值：对叶子结点赋予的一个有意义的数值量。

路径长度：从树中一个结点到另一个结点之间的分支数目称作路径长度。

树的路径长度：从树根到每一结点的路径长度之和。

树的带权路径长度：设树具有n个带权值的 叶子结点，从根节点到各个叶子结点的路径长度与相应叶子结点权值的乘积之和称为树的带权路径长度。记为：
$WPL={\sum }_{i=0}^n{w}_k{l}_k$,
其中$w_k$为第k个叶子结点的权值，$l_k$为从根结点到第k个叶子结点的路径长度。

赫夫曼树：带权路径长度WPL最小的二叉树称作赫夫曼树或哈夫曼树或最优二叉树。

2、赫夫曼树的特点

1、权值越大的叶子结点越靠近根结点，而权值越小的叶子结点越远离根结点。

2、赫夫曼树只有度为0（叶子结点）和度为2（分支结点）的结点，不存在度为1的结点。

3、赫夫曼算法

赫夫曼算法——构造赫夫曼树——基本思想：

• 1、初始化:由给定的n个权值{ $w_1,w_2,...,w_n$}构造只有一个根结点，左、右子树为空的二叉树，从而得到一个二叉树集合F={ $T_1,T_2,...,T_n$}；
• 2、选取与合并：在F中选取根结点的权值最小的两棵二叉树分别作为左、右子树构造一棵新的二叉树，这棵新二叉树的根结点的权值为其左、右子树根结点的权值之和；
• 3、删除与加入：在F中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到F中；
• 4、重复2、3两步，当集合F中只剩下一棵二叉树时，这棵二叉树便是赫夫曼树。

例子：



集合中剩下的最后一棵二叉树便是赫夫曼树。

伪代码：

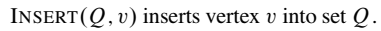
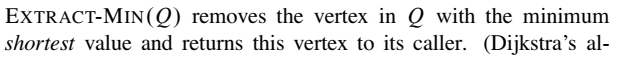
python 实现之

def Build_Huffman_Tree(char,freq,n):#char:叶子结点，freq:权值    Q=[]    for i in range(n):        z=[]        z.append(char[i])        z.append(freq[i])        Q.append(z)     for _ in range(n-1):        Q=sorted(Q,key=lambda x:x[1])        x=EXTRACT_MIN(Q)        Q.remove(Q[0])        Q=sorted(Q,key=lambda x:x[1])        y=EXTRACT_MIN(Q)        Q.remove(Q[0])        z=[x[0]+y[0],x[1]+y[1]]        INSERT(Q,z)        print(Q)    return EXTRACT_MIN(Q)[1]def EXTRACT_MIN(Q):    x=Q[0]    return xdef INSERT(Q,z):    Q.append(z)    return Qchar=[1,5,2,10]freq=[10,6,2,0.2]n=4Build_Huffman_Tree(char,freq,n)

结果：

[[5, 6], [1, 10], [12, 2.2]][[1, 10], [17, 8.2]][[18, 18.2]]Process finished with exit code 0

霍夫曼编码(Huffman Codes)
通过霍夫曼树来构造的编码称为哈弗曼编码（huffman code）。

霍夫曼编码是一种编码方法，属于一种程序算法。
霍夫曼编码是 可变字长编码(VLC) 的一种，由霍夫曼提出，又称之为最佳编码。在计算机数据处理中，霍夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码。
霍夫曼编码是霍夫曼树在通讯领域的经典应用之一。
霍夫曼编码广泛用于数据文件的压缩，压缩率通常在20% 到90%，通常数据的重复率越高，那么压缩率就越高。
霍夫曼编码(Huffman Codes)的基本步骤：

利用字符集中每个字符的使用频率作为权值构造一个哈夫曼树；
从根结点开始，为到每个叶子结点路径上的左分支赋予0，右分支赋予1，并从根到叶子方向形成该叶子结点的编码。