本文共 31976 字，大约阅读时间需要 106 分钟。

1.what Are Algorithms and why should you care?

1.1Algorithms-what?

俗称：算法是完成任务的一组步骤。

1.2Algorithms-get?

给一个问题一个输入，他总是应该为该问题提供正确的解决方案，并且应该同时有效的利用计算资源。

1.3Algorithms-correctness

给出对应问题的正确解。（如果能够控制错误解的执行频率，我们可以接受计算机算法可能会产生错误的答案）

Loop invariants
循环不变式可以帮助我们辩解算法的正确性。
循环不变式的三条性质：
初始化：循环的第一次迭代之前，它为真。
保持：如果循环的某次迭代之前它为真，那么下次迭代之前它仍为真。
终止：在循环终止时，不变式为我们提供一个有用的性质，该性质有助于证明算法是正确的。

正确性correctness是另一类算法的棘手问题，称为近似算法。
近似算法适用于优化问题。

2.How to Decribe and Evaluate Compute Algorithms?

2.1How to Decribe Compute Algorithms?

将计算机算法描述为使用常用编程语言（例如Java,C,C++,python等）的可运行程序。

2.2How to Evaluate Compute Algorithms?

常用时间复杂度与空间复杂度评估算法

2.3Recurion

递归：其实就是函数调用其本身来实现某些算法。
每个递归定义必须至少有一个条件，当满足条件时递归不再进行。 递归的优点：结构更清晰，代码更简洁，更容易让人理解，从而减少代码的阅读时间。
例子：计算n!
伪代码

python

def factional(n):    if n==0:        return 1    else:        return n*factional(n-1)    

3. Algorithms for Sorting and Searching

3.1Algorithms-search（搜索）

3.1.1线性搜索linear-search

（遍历所有的数据）
伪代码：

python

def linear_search(A,x):    n=len(A)    answer = "NOT FOUND"    for i in range(n):        if A[i]==x:            answer=i    return answer

递归法实现线性搜索

def Recursive_linear_search(A,i,x):    n=len(A)    if i>n:        return "NOT-FOUND"    else :        if A[i]==x:            return i        else:            return  Recursive_linear_search(A,i+1,x)   

输入函数中i=0

3.1.2较好的线性搜索better-linear-search

(找到值就不再遍历，跳出循环)
伪代码

python

def better_linear_search(A,x):    n=len(A)    for i in range(n):        if A[i]==x:            return i    return print("NOT FOUND")    

3.1.3哨兵线性搜索sentinel-linear-search

(在最后的位置上放置一个空盒子，并令这个变量等于x即我们要寻找的值：这样可以减少判断i《n的循环)
伪代码

python

def sentinel_linear_search(A,x):    n=len(A)    last=A[n-1]#b保存数组最后一个元素    A[n-1]=x#用x替换数组最后一个元素    i=0    while A[i]!=x:        i+=1    A[n-1]=last#还原数组最后一个元素    if i<n-1 or A[n-1]==x:        return i     else:        print("NOT FOUND")

3.1.4二分查找/二分搜索Binary search

(要求数组已排序)
假设表中元素是有序的，将表的中间位置的关键字与所需的关键字比较，相等则成功，否则分为前后两个子表，若所需的值大于中间元素，则在后半部分查找，否则在前半部分查找。重复上述过程，直到查询到结果。需要两个指针p,r
优点：比较次数少，速度快
缺点：要求待查表为有序表。
时间复杂度：O(logn)
伪代码

#非递归实现import numpy as npdef binary_search(A,x):    A=np.sort(A)#先将A排序    n=len(A)    p=1#p:头指针    r=n-1#r:尾指针    while p<=r:        q=(p+r)//2#//符号：商取整        if A[q]==x:            return q        elif A[q]>x:            r=q-1        else:            p=q+1    return print("NOT FOUND")

#递归实现(p,r)一般刚开始是（0，len(A)_1)也就是列表中第一个与最后一个位置def recursive_binary_search(A,p,r,x):    A=np.sort(A)#先将A排序    if p>r:        return print("NOT FOUND")    else:        q=(p+r)//2        if A[q]==x:            return q        elif A[q]>x:            return recursive_binary_search(A,p,q-1,x)        else:            return recursive_binary_search(A,q+1,r,x)   

3.2Algorithms-sort（排序）

4.A Lower Bound for Sorting and How to Beat It

4.1Rules for sorting

1.比较排序：元素的排序键比较大小，如归并排序，快排等
2.排序键为固定的几个值：如每个排序键为1或2，并且元素仅由排序键构成，而没有卫星数据。对于这样的数组来说，采用Really-simple-sort。
伪代码

def really_simple_sort(A):    k=0    for i in range(len(A)):        if A[i]== 1:            k+=1    for i in range(k):        A[i]=1    for i in range (k+1,len(A)):        A[i]=2    return A

时间复杂度：Θ(n）

4.2Beating the lower bound

突破时间的下限：
1.排序键只有两个可能的值，每一个元素仅由一个排序键构成，没有卫星数据；在此限制的情况下，我们可以仅用Θ(n）对n个元素排序，而无需比较元素。如Really-simple-sort。
2.推广：排序键是m个连续整数（例如0到m）范围内的整数，并且还可以允许元素具有卫星数据。如计数排序Count sort，基数排序Radix sort。

5 Directed Acyclic Graphs

5.1 Graphs

1.
2.Directed Acyclic Graphs
The directed graphs that we have seen have another property: there
is no way to get from a vertex back to itself by following a sequence
of one or more edges. We call such a directed graph a directed acyclic
graph, or dag.

5.2 Algorithm-Topological sorting

定义：对于一个有向无环图G=(V,E)来说，其拓扑排序是G中所有顶点的一种线性次序，该次序满足如下条件：如果图G包含边（u，v)，则顶点u在拓扑排序中处于顶点v的前面。
特点：由拓扑排序产生的线性次序不一定是唯一的。
实现：使用深度优先搜索DFS可对有向无环图进行拓扑排序或者是按照入度为0的顶点。

伪代码：

python：

def Topological_sort(G):    in_degrees = dict((u, 0) for u in G)#创建入度字典并将入度初始化为0    for u in G:        for v in  G[u]:            in_degrees[v] += 1                                    # 每一个节点的入度    NEXT = [u for u in G if in_degrees[u] == 0]                                    # 入度为 0 的节点放到NEXT列表中    S = []                          # 创建一个空列表    while NEXT:                    # NEXT非空时        u = NEXT.pop()                 # 默认从最后一个移除 list.pop()                                            S.append(u)                 #将取出的元素放在列表S中        for v in G[u]:            in_degrees[v] -= 1                                    # 并移除其指向            if in_degrees[v] == 0:                NEXT.append(v)    return SG = {       'a':'bf',    'b':'cdf',    'c':'d',    'd':'ef',    'e':'f',    'f':''}Topological_sort(G)

时间复杂度：$\Theta (n+m)$

5.3 Critical path

关键路径：关键路径是在所有路径上任务时间总和最大的路径。

6 Shortest Paths

1.从某个源点到其余各顶点的最短路径
2.找到每对顶点之间的最短路径。

6.1 Algorithm-Dijkstra’s algorithm

目的：
给定一个图和图中的一个源顶点，找到从源到给定图中所有顶点的最短路径。

特点：
1.边权重非负。
2.图可能包含循环。

伪代码：
算法步骤如下：
G={V,E}

1. 初始时令 S={V0},T=V-S={其余顶点}，T中顶点对应的距离值D
   若存在<V0,Vi>，d(V0,Vi)为<V0,Vi>弧上的权值
   若不存在<V0,Vi>，d(V0,Vi)为∞
2. 从T中选取一个与S中顶点有关联边且权值最小的顶点W，加入到S中
3. 对其余T中顶点的距离值进行修改：若加进W作中间顶点，从V0到Vi的距离值缩短，则修改此距离值
   重复上述步骤2、3，直到S 中包含所有顶点，即W=Vi为止

python：

import sys '该模块提供对解释器使用或维护的一些变量的访问，以及与解释器强烈交互的函数。它始终可用。'class Graph(): #定义图类      def __init__(self, vertices):         self.V = vertices         self.graph = [[0 for column in range(vertices)]                      for row in range(vertices)]       def printSolution(self, dist):         print("Vertex \tDistance from Source")        for node in range(self.V):             print(node, "\t", dist[node] )      # A utility function to find the vertex with      # minimum distance value, from the set of vertices      # not yet included in shortest path tree     def minDistance(self, dist, sptSet):           # Initilaize minimum distance for next node         min = sys.maxsize #平台的Py_ssize_t类型支持的最大正整数          # Search not nearest vertex not in the          # shortest path tree         for v in range(self.V):             if dist[v] < min and sptSet[v] == False:                 min = dist[v]                 min_index = v           return min_index       # Funtion that implements Dijkstra's single source      # shortest path algorithm for a graph represented      # using adjacency matrix representation     def dijkstra(self, src):           dist = [sys.maxsize] * self.V         dist[src] = 0        sptSet = [False] * self.V           for cout in range(self.V):               # Pick the minimum distance vertex from              # the set of vertices not yet processed.              # u is always equal to src in first iteration             u = self.minDistance(dist, sptSet)               # Put the minimum distance vertex in the              # shotest path tree             sptSet[u] = True              # Update dist value of the adjacent vertices              # of the picked vertex only if the current              # distance is greater than new distance and             # the vertex in not in the shotest path tree             for v in range(self.V):                 if self.graph[u][v] > 0 and sptSet[v] == False and dist[v] > dist[u] + self.graph[u][v]:                         dist[v] = dist[u] + self.graph[u][v]           self.printSolution(dist)   # Driver program g = Graph(9) g.graph = [[0, 4, 0, 0, 0, 0, 0, 8, 0],         [4, 0, 8, 0, 0, 0, 0, 11, 0],         [0, 8, 0, 7, 0, 4, 0, 0, 2],         [0, 0, 7, 0, 9, 14, 0, 0, 0],         [0, 0, 0, 9, 0, 10, 0, 0, 0],         [0, 0, 4, 14, 10, 0, 2, 0, 0],         [0, 0, 0, 0, 0, 2, 0, 1, 6],         [8, 11, 0, 0, 0, 0, 1, 0, 7],         [0, 0, 2, 0, 0, 0, 6, 7, 0]         ];   g.dijkstra(0); 

6.2Algorithm-Bellman-Ford algorithm

目的：查找从单个源顶点到所有其他顶点的最短路径，确定图是否包含负权循环。

特点：

• 非常简单的方法，边缘权重可以是负的。

• 可以使用Bellman-Ford算法的结果来确定图是否包含负权循环，如果包含负权循环， 以识别循环中的顶点和边。

伪代码：
算法步骤如下：
输入：图和源顶点src
输出：从src到所有顶点的最短距离。如果存在负权循环，则不计算最短距离，报告负权循环。Create an array dist[] of size |V| with all values as infinite except dist[src] where src is source vertex.

• 1.创建一个大小为顶点总数的多维数组dist[]记录源顶点到各顶点的距离,并初始化源顶点到其他顶点的距离为无穷远，到自身的距离为0。

• 2.此步骤计算最短距离。重复以下步骤| V |-1次，其中| V |是给定图中的顶点数。

  • 对每一边 edge u-v作以下松弛操作：
    如果dist[v] > dist[u] + weight of edge uv，
    则更新dist[v]：dist[v] = dist[u] + weight of edge uv

• 3.此步骤报告图中是否存在负权重循环。对每个边u-v执行以下操作：

  • 如果dist[v]>dist[u]+边uv的权重，则“图形包含负权重循环”

注：步骤3的思想是，如果图不包含负权循环，步骤2保证最短距离。如果我们再遍历所有边一次，得到任意顶点的较短路径，则存在一个负权循环。

python:

class Graph:        def __init__(self, vertices):          self.V = vertices # No. of vertices          self.graph = []        # function to add an edge to graph      def addEdge(self, u, v, w):          self.graph.append([u, v, w])                # utility function used to print the solution      def printArr(self, dist):          print("Vertex Distance from Source")          for i in range(self.V):              print("{0}\t\t{1}".format(i, dist[i]))            # The main function that finds shortest distances from src to      # all other vertices using Bellman-Ford algorithm. The function      # also detects negative weight cycle      def BellmanFord(self, src):            # Step 1: Initialize distances from src to all other vertices          # as INFINITE          dist = [float("Inf")] * self.V          dist[src] = 0            # Step 2: Relax all edges |V| - 1 times. A simple shortest          # path from src to any other vertex can have at-most |V| - 1          # edges          for _ in range(self.V - 1):              # Update dist value and parent index of the adjacent vertices of              # the picked vertex. Consider only those vertices which are still in              # queue              for u, v, w in self.graph:                  if dist[u] != float("Inf") and dist[u] + w < dist[v]:                          dist[v] = dist[u] + w            # Step 3: check for negative-weight cycles. The above step          # guarantees shortest distances if graph doesn't contain          # negative weight cycle. If we get a shorter path, then there          # is a cycle.            for u, v, w in self.graph:                  if dist[u] != float("Inf") and dist[u] + w < dist[v]:                          print("Graph contains negative weight cycle")                         return                                  # print all distance          self.printArr(dist)    g = Graph(5)  g.addEdge(0, 1, -1)  g.addEdge(1, 0, -1)  g.addEdge(1, 2, 3)  g.addEdge(1, 3, 2)  g.addEdge(1, 4, 2)  g.addEdge(3, 2, 5)  g.addEdge(3, 1, 1)  g.addEdge(4, 3, -3)    # Print the solution  g.BellmanFord(0) 

输出结果：
Graph contains negative weight cycle

6.3 Floyd-Warshall algorithm

目的： 在给定的带权有向图中求对顶点之间的最短距离。
python:

在这里插入代码片

**时间复杂度：**O($n^3$)

参考资料：
https://zh.wikipedia.org/wiki/%E6%88%B4%E5%85%8B%E6%96%AF%E7%89%B9%E6%8B%89%E7%AE%97%E6%B3%95

https://www.geeksforgeeks.org/dijkstras-shortest-path-algorithm-greedy-algo-7/

7 Algorithms on String

7.1

7.2 Longest common subsequence

最长公共子序列，简称LCS

基本概念：

• 序列：按某种顺序排列的一张表。
• 子序列：一个字符串 s 被称作另一个字符串 S 的子序列，说明从序列 S 通过去除某些元素但不破坏余下元素的相对位置（在前或在后）可得到序列 s 。有m个不同字符的字符串有$2^m$个子序列。
• 子串：串中任何连续字符组成。一个字符串 s 被称作另一个字符串 S 的子串，表示 s 在 S 中出现了。
  注：子串与子序列的概念不同，例子：对于字符串CATCGA，子序列ATCG是子字符串，但子序列CTCA不是。
• 公共子序列(common subsequence): 给定序列X和Y，序列Z是X的子序列，也是Y的子序列，则Z是X和Y的公共子序列。
• LCS:给定序列X和Y,从它们的所有公共子序列中选出长度最长的那一个或几个。
• 最长公共子串：LCS与最长公共子串的区别是子串要求连续的，子序列不需要连续。
• 前缀：给定一个序列X=[$x_1$,$x_2$,$x_3$,…,$x_m$],X的第i前缀为$X_i$=[$x_1$,$x_2$,$x_3$,…,$x_i$]。

Question:给定两个字符串X与Y，找出X与Y的LCS？
方法：
动态归划：其基本思想将待求解问题分解成若干个子问题，先求解子问题，然后从这些子问题的解得到原问题的解。

特征分析：
LCS的最优子结构：

7.2.1 Algorithm-Computing the length of an LCS

计算𝑋𝑖,𝑌𝑗 两者LCS的长度

伪代码：

python：

import numpy as npdef compute_lcs_table(X,Y):    m=len(X)    n=len(Y)    l=np.zeros((m+1,n+1),dtype=np.int)    for i in range(1,m+1):        for j in range(1,n+1):            if X[i-1]==Y[j-1]:#python 对列表的索引从0开始，指向数组的索引                l[i,j]=l[i-1,j-1]+1            else:                l[i,j]=max(l[i,j-1],l[i-1,j])    return l                

时间复杂度：$\Theta (mn)$
its lowerright entry, $l[m,n]$, gives us the length of an LCS of X and Y.

7.2.2 Algorithm- Constructing an LCS

伪代码：

python：

def assemble_lcs(X,Y, l,i,j):#i,j分别指向X和Y的索引，以及数组LCS_length的索引    if  l[i,j]==0:#最长公共子序列长度为0        return     if X[i-1]==Y[j-1]:        assemble_lcs(X,Y, l,i-1,j-1)        print(X[i-1],end="")#输出不换行    elif X[i-1]!=Y[j-1]and  l[i,j-1]> l[i-1,j]:         assemble_lcs(X,Y, l,i,j-1)    elif X[i-1]!=Y[j-1]and l[i,j-1]<= l[i-1,j]:#=号时向上走         assemble_lcs(X,Y, l,i-1,j)

时间复杂度：O(m+n)
LCS总时间复杂度：$\Theta (mn)$+O(m+n)

7.3 Tranfroming one string to another

Question：字符串X转换为字符串Y
基本操作：
1.建立一新空字符串Z，使Y与Z相同
2.复制，替代，删除，插入

3.定义$X_i$转换为$Y_j$最优方法的代价为cost[i,j].
4.计算代价表
伪代码：

python：

def Computer_Transform_Tables(X,Y,Cc,Cr,Cd,Ci):#参数为两字符串，操作代价：复制，替代，删除，插入    m=len(X)    n=len(Y)    cost= np.zeros((m+1, n+1), dtype=np.int)    op= np.zeros((m+1, n+1), dtype="<U16")#字符串类型    for i in range(1,m+1):        cost[i,0]=i*Cd        op[i,0]='del '+X[i-1]    for j in range(1,n+1):        cost[0,j]=j*Ci        op[0,j]='ins '+Y[j-1]    for i in range(1,m+1):        for j in range(1,n+1):            if X[i-1]==Y[j-1]:                cost[i,j]=cost[i-1,j-1]+Cc                op[i,j]='copy '+X[i-1]            else:                cost[i,j]=cost[i-1,j-1]+Cr                op[i,j]='rep '+X[i-1]+" by "+Y[j-1]            if cost[i-1,j]+Cd<cost[i,j]:                cost[i,j]=cost[i-1,j]+Cd                op[i,j]='del '+X[i-1]            if cost[i,j-1]+Ci<cost[i,j]:                cost[i,j]=cost[i,j-1]+Ci                op[i,j]='ins '+Y[j-1]    return cost,op

5.重组
伪代码：

python：

def Assemble_Transformatiomn(X,Y,op,i,j):    if i==0 and j==0:        return     else:        if op[i,j]=='copy '+X[i-1] or op[i,j]=='rep '+X[i-1]+' by '+Y[j-1]:            Assemble_Transformatiomn(X,Y,op,i-1,j-1)            print(op[i,j])        elif op[i,j]=='del '+X[i-1]:            Assemble_Transformatiomn(X,Y,op,i-1,j)            print(op[i,j])        elif op[i,j]=='ins '+Y[j-1]:            Assemble_Transformatiomn(X,Y,op,i,j-1)            print(op[i,j])        

7.4 String matching

Question：
T：a text string(consist of n characters) T=$t_1{t}_2...t_n$
P: a pattern string(consist of m characters) P=$p_1{p}_2...p_m$
m<=n
找出模板P在文本T中出现的所有位置即偏移值。
偏移：若$ts+1=p1$,$ts+2=p2$…$ts+m=pm$,则P以偏移值s出现在文本T中。

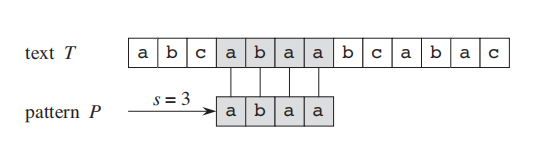
常见算法：

7.4 .1 Algorithm-Naive

朴素字符串匹配算法，又称暴力匹配法:
通过一个循环找到所有有效偏移，该循环对 𝑛−𝑚+1 个可能的s值进行检测，看是否满足条件 𝑃[1…𝑚]=𝑇[𝑠+1,…,𝑠+𝑚]
伪代码：

python：

def naive_string_matcher(T,P):#输入文本与模板字符串    n=len(T)    m=len(p)    for s in range(n-m+1):        if p[1:m]==T[s+1:s+m]:            print('pattern occurs with shift',s)

缺点：朴素算法效率不高，无效的s值存在时，浪费时间

优点：不需要预处理

7.4 .2 Algorithm-Rabin-Karp

步骤：
1.预处理：

• 预处理就是计算出字符串m的哈希值，我们计算哈希值的算法就是把这些字符关联在一个多项式里面；
• 多项式的模式就是 m[0]*x^lm-1 + m[1]*x^lm-2 + … + m[lm-1]*x^0 这种形式的，这样就把一串字符关联在了一个多项式里面；
• 然后我们利用霍纳法则优化多项式的计算，这样的话，我们可以在O(m)时间内，计算出字符串的哈希值

2.搜索

• 搜索的话就是从字符串n里面第一个lm长的字符串开始，不断地比较这个字符串与字符串m的哈希值，如果哈希值相等的话，
• 就再去一个字符一个字符的比较一下是否相等，这样，我们最快，可以在O(n-m+1)的时间内比较完，最坏的情况是O((n-m+1)*m)
• 但是平均时间来看，rk算法要比朴素算法快得多

关键点：

• 1.哈希算法的关键，就是计算关联这一串字符串的多项式，每个字符值都是多项式的一个系数
• 2.利用霍纳法则优化多项式的计算
• 3.如果明白了哈希值的计算是多项式相加的结果，就不难明白计算n字符串里面其余lm长度字符串大小的哈希值的算法了。
  伪代码：
  
  python：

def Rabin_Kapp_Matcher(pat, txt, q,d):     M = len(pat)     N = len(txt)     i = 0    j = 0    p = 0    # hash value for pattern     t = 0    # hash value for txt     h = 1      # The value of h would be "pow(d, M-1)%q"     for i in range(M-1):         h = (h*d)%q       # Calculate the hash value of pattern and first window     # of text     for i in range(M):         p = (d*p + ord(pat[i]))%q         t = (d*t + ord(txt[i]))%q       # Slide the pattern over text one by one     for i in range(N-M+1):         # Check the hash values of current window of text and         # pattern if the hash values match then only check         # for characters on by one         if p==t:             # Check for characters one by one             for j in range(M):                 if txt[i+j] != pat[j]:                     break              j+=1            # if p == t and pat[0...M-1] = txt[i, i+1, ...i+M-1]             if j==M:                 print("Pattern found at index " + str(i))          # Calculate hash value for next window of text: Remove         # leading digit, add trailing digit         if i < N-M:             t = (d*(t-ord(txt[i])*h) + ord(txt[i+M]))%q               # We might get negative values of t, converting it to             # positive             if t < 0:                 t = t+q

7.4 .3 Algorithm-Finite Automata

有限自动机（finite automaton），简称FA，只是状态和基于输入序列的从一个状态到另一个状态的方法。

在我们的字符串匹配应用程序中，输入序列将是 文本T的字符，FA将有𝑚+1个状态， 比模式P中出现的字符数多1，从0到m。

FA从状态0开始。当它处于k状态时，k 它使用的最新文本字符与模式的前k个字符匹配 。因此，每当FA进入m状态时 在文中看到了整个模式。

FA在内部存储一个表next-state，它由所有状态(m+1个）和文本T中所有可能的输入字符(总数记为q)构成一个二维表。

𝑛𝑒𝑥𝑡−𝑠𝑡𝑎𝑡𝑒[𝑠,𝑎]表示FA当前处于s状态，则要移动到的状态的编号它刚刚消耗了文本中的字符a。
1.预处理：填充next—state
伪代码：

python：

import pandas as pdimport numpy as npdef next_state(T,P):    m=len(p)    different=list(set(T))#将文本T不重复的字符转化为列表 set函数创建不重复元素集合    q=len(different)#文本T中所有可能的输入字符    next_state=pd.DataFrame(np.zeros((m+1,q),dtype=np.int),index=[x for x in range(m+1)],columns=different)    state=0    while state<m:        for x in different:            j=min(state+1,m)            while j>0:                pka=p[:j-1]+x#更新后的字符                if pka==p[:j]:#前缀等于后缀                    next_state.loc[state,x]=j                    break                j-=1        state+=1    next_state.loc[m,p[0]]=1    return next_state

2.匹配：

python：

def fa_string_matcher(T,next_state,m):    n=len(T)    state=0    for i in range(n):        t_i=T[i]        state=next_state.loc[state,t_i]        if state==m:            print('pattern occurs with shift %d'%(i-m+1))        

7.4 .4 Algorithm-Knuth-Morris-Pratt

基本概念：

• 最长前缀后缀(Longest Prefix Suffix)
  即 最长相等前后缀长度
  

• next数组：把模式串各个位置的i值的变化定义为一个next数组。next数组的数值只与模式串本身有关。next[i]=j,含义是：下标为i 的字符前的字符串最长相等前后缀的长度为j。
  例子：模式串p= "abcabcmn"的next数组为next[0]=-1(前面没有字符串单独处理)，next[1]=0；next[2]=0；next[3]=0；next[4]=1；next[5]=2；next[6]=3；next[7]=0。
  

解题步骤：
1.预处理：
计算next数组。

接下来，假设我们从左到右依次计算next数组，在某一时刻，已经得到了next[0]~next[i],现在要计算next[i+1]，设j=next[i]，由于知道了next[i]，所以我们知道T[0,j-1]=T[i-j,i-1],现在比较T[j]和T[i]，如果相等，由next数组的定义，可以直接得出next[i+1]=j+1。
python：

def gen_next(p):    j,k,m=0,-1,len(p)    next=[-1]*m    #j表示p中的第几个元素，k表示当前元素前面子串中最长公共前缀长度后的字符索引    while j <m-1:        if k==-1 or p[j]==p[k]:            k,j=k+1,j+1            next[j]=k        else:            k=next[k]    return next    

2.匹配
当模式串中的某个字符跟文本串中的某个字符匹配失配时，模式串下一步应该跳到哪个位置。如模式串中在j 处的字符跟文本串在i 处的字符匹配失配时，下一步用next [j] 处的字符继续跟文本串i 处的字符匹配，相当于模式串向右移动 j - next[j] 位。
python：

def matching_KMP(t,p,next):    """KMP串匹配，主函数"""    i,j=0,0    n,m=len(t),len(p)    while i<n and j<m:        if j==-1 or t[i]==p[j]:            i,j=i+1,j+1        else:            j=next[j]        if j==m:            print("pattern occurs with shift %d"%(i-j))            j=0

KMP算法通过一个预处理来构建一个模式串p的前缀数组（即计算字符串p每一个位置的字符串的前缀和后缀公共部分的最大长度，不包括字符串本身，否则最大长度始终是字符串本身）
接下来的匹配过程会不断地使用到该前缀数组（而且对于主串T只需遍历一次），使匹配的复杂度降为O(n+m)

8 Foundations of Cryptography

密码学基础：
1.encryption(加密):converts plaintext to ciphertext.
2.decryption(解密):converts ciphertext back to its original plaintext.

基本术语：
1.plaintext(明文）：the original information
2.ciphertext(密文)：the encryptd version
3.key:the information needed to convert

加密方式有以下几种：

8.1Simple substitution cipher

简单替换式密码
定义：通过将每个字符转换成其他的、唯一的字符（但不一定是在字母表后面出现固定位置的字符），使密码更安全一些。
例子：
plaintext: Send me a hundred more soldiers
ciphertext: Krcz sr h byczxrz sfxr kfjzgrxk
解密的人只要与加密的人有共同的密钥，就可以解密。

密码系统有两种，对称密钥密码系统和非对称密钥密码系统。

8.2 Symmetric-key cryptography

对称密钥密码学
1.定义:对称加密算法即，加密和解密使用相同密钥的算法。（加密Key=解密key）；对称密钥算法又分为分组密码 (Block Cipher)和流密码(Stream Cipher)。

• 序列密码（stream cipher，流加密）:一次加密明文中的一个位;序列密码是由一种专业的密码，一次性密码本（one-time pads）发展而来的。
• 分组密码（block cipher，块加密）:一次加密明文中的一个块
  ①电子编码本（ECB: Electronic Code Book ）
  ②密码分组链接（CBC: Cipher Block Chaining ）
  ③密码反馈（CFB: Cipher Feedback ）
  ④输出反馈（OFB: Output Feedback ）

2.Stream cipher : One-time pads（OPT）

一次型密码在位上工作，一个位只能接受两个值：0和1。

OPT apply the XOR（exclusive-or）, operation to bits.
①if x is a bit, then x⊕0=x and x⊕1 gives the opposite of x ;
②if x and y are bits, then (x⊕y)⊕y=x : XORing x with the same value twice gives x.

• 异或是一个数学运算符。它应用于逻辑运算。异或的数学符号为“⊕”，其运算法则为：
  a⊕b = (¬a ∧ b) ∨ (a ∧¬b)
• 如果a、b两个值不相同，则异或结果为1。如果a、b两个值相同，异或结果为0。
• 异或也叫半加运算，其运算法则相当于不带进位的二进制加法：二进制下用1表示真，0表示假，则异或的运算法则为：0⊕0=0，1⊕0=1，0⊕1=1，1⊕1=0（同为0，异为1），这些法则与加法是相同的，只是不带进位，所以异或常被认作不进位加法。

例子：
加密

解密：

要求：

• 密钥所需的位与明文所需的位一样多
• 这些位应该随机选择
• 密钥钥需要事先在双方之间共享。

3.Block ciphers

分组密码
1.定义：
他们使用一个较短的键，然后将明文分割成几个块，依次对每个块应用该键。也就是说，他们认为明文是l块t1，t2，t3，…，tl，并且他们将这些明文块加密成密文的l块c1，c2，c3，…，cl。这种系统被称为分组密码。每次只能处理特定长度的一块数据的密码算法（一块是指分组），一个分组的比特数称为分组长度；处理完一个分组就结束了，不需通过内部状态来记录加密的进度。
2.分组密码的模式：

分组密码只能加密固定长度的分组，需要加密的明文长度可能超过分组密码的分组长度，此时就需要对分组密码算法进行迭代，以便将长明文进行加密，迭代的方法就称为分组密码的模式。

1）ECB（电子密码本模式）：
ECB 模式是最简单的加密模式，明文消息被分成固定大小的块（分组），并且每个块被单独加密。每个块的加密和解密都是独立的，且使用相同的方法进行加密，所以可以进行并行计算，但是这种方法一旦有一个块被破解，使用相同的方法可以解密所有的明文数据，安全性比较差。适用于数据较少的情形，加密前需要把明文数据填充到块大小的整倍数。

ECB算法优点：简单、孤立，每个块单独运算。适合并行运算。传输错误一般只影响当前块。

ECB算法缺点：同明文输出同密文，可能导致明文攻击。

2）CBC模式（密码分组链接：Cipher-block chaining）
CBC 模式中每一个分组要先和前一个分组加密后的数据进行XOR异或操作，然后再进行加密。这样每个密文块依赖该块之前的所有明文块，为了保持每条消息都具有唯一性，第一个数据块进行加密之前需要用初始化向量（initialization vector or IV ）进行异或操作。CBC模式是一种最常用的加密模式，它主要缺点是加密是连续的，不能并行处理，并且与ECB一样消息块必须填充到块大小的整倍数。

初始化向量（IV）：在加密第一个明文分组时，需要事先准备一个长度为一个分组的比特序列代替；每次加密时，都会随机产生一个不同的比特序列作为初始化向量。

CBC算法优点：串行化运算，相同明文不同密文。

CBC算法缺点：需要初始向量。

3）CFB模式(密文反馈:Cipher feedback)

CFB 模式和CBC模式比较相似，前一个分组的密文加密后和当前分组的明文XOR异或操作生成当前分组的密文。CFB模式的解密和CBC模式的加密在流程上其实是非常相似的。

CFB算法优点：同明文不同密文，分组密码转换为流密码。

CFB算法缺点：串行运算不利并行，传输错误可能导致后续传输块错误。

4）OFB模式（输出反馈：Output feedback）
OFB 模式将分组密码转换为同步流密码，也就是说可以根据明文长度先独立生成相应长度的流密码。通过流程图可以看出，OFB和CFB非常相似，CFB是前一个分组的密文加密后XOR当前分组明文，OFB是前一个分组与前一个明文块异或之前的流密码XOR当前分组明文。由于异或操作的对称性，OFB模式的解密和加密完全一样的流程。

OFB算法优点：同明文不同密文，分组密码转换为流密码。

OFB算法缺点：串行运算不利并行，传输错误可能导致后续传输块错误。

8.3对称密钥算法

常用算法包括DES(Data Encryption Standard，数据加密算法) 、3DES(Triple Data Encryption Algorithm，三重数据加密算法)、 AES(Advanced Encryption Standard，高级加密标准，又称Rijndael加密法) 、PBE(Password-based encryption，基于密码验证)、RC4（来自Rivest Cipher 4的缩写）、 SM1 、SM4（国产）

8.4Public-key cryptography

公钥密码学，又称非对称密钥密码学
1.定义:
非对称密码体制也叫公开密钥密码体制、双密钥密码体制。其原理是加密密钥与解密密钥不同，形成一个密钥对，用其中一个密钥加密的结果，可以用另一个密钥来解密 。

目前普遍使用的非对称加密算法主要有RSA、Elgamal（离散对数）、ECC（椭圆曲线）等

2.特点：

加密和解密使用不同的密钥；一个密钥公开，称公钥a public key （P）；一个密钥保密，称私钥a secret key（S）。

公钥和密钥有一种特殊的关系：
$t=F_s(F_p(t))$：如果您使用我的公钥将明文加密为密文，然后我使用我的密钥解密密文，我将得到原始明文。
$t=F_p(F_s(t))$：如果我用我的密钥加密明文，任何人都可以解密密文

其他人的公钥和私钥也一样：公钥函数FP是有效可计算的，但只有密钥持有者才能合理地计算密钥函数FS。

3.优点：

密钥分配，不必保持信道的保密性 ；可以用来签名和防抵赖

4.比较：

• 对称密码中加密与解密使用的是同样的密钥，所以速度快，但由于需要将密钥在网络传输，所以安全性不高。

• 非对称密码中使用了一对密钥，公钥与私钥，所以安全性高，但加密与解密速度慢。

5.常用算法：

RSA 、ECC、 DSA（Digital Signature Algorithm）

The RSA cryptosystem

1.RSA算法

1977年，三位数学家Rivest、Shamir 和 Adleman 设计了一种算法，可以实现非对称加密。这种算法用他们三个人的名字命名，叫做RSA算法。从那时直到现在，RSA算法一直是最广为使用的"非对称加密算法"。毫不夸张地说，只要有计算机网络的地方，就有RSA算法。

这种算法非常可靠，密钥越长，它就越难破解。根据已经披露的文献，目前被破解的最长RSA密钥是768个二进制位。也就是说，长度超过768位的密钥，还无法破解（至少没人公开宣布）。因此可以认为，1024位的RSA密钥基本安全，2048位的密钥极其安全。

RSA依赖于数论的多个方面，其中许多与模块化算法有关。

2.数学基础
为了使RSA满足公钥密码体制的标准，与质数有关的两个数论性质必须成立。
1）RSA依赖的第一个属性是，如果您有一个数字是两个大的秘密质数的乘积，那么没有其他人可以在任何合理的时间内确定这些因素。（大数分解）
2）第二个属性是，即使很难计算一个大质数，但不难确定一个大数是否是质数。（素数判定）
两种方法：
①AKS primality test : O($n^c$)
②Miller-Rabin primality test : $2^{5}0$
modular arithmetic(模运算）

质数

除了1和该数自身外，无法被其他自然数整除的数（也可定义为只有1该数本身两个正因数]的数）。

互质关系

如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系（coprime）。比如，15和32没有公因子，所以它们是互质关系。这说明，不是质数也可以构成互质关系。

关于互质关系，不难得到以下结论：

1. 任意两个质数构成互质关系，比如13和61。

2. 一个数是质数，另一个数只要不是前者的倍数，两者就构成互质关系，比如3和10。

3. 如果两个数之中，较大的那个数是质数，则两者构成互质关系，比如97和57。

4. 1和任意一个自然数是都是互质关系，比如1和99。

5. p是大于1的整数，则p和p-1构成互质关系，比如57和56。

6. p是大于1的奇数，则p和p-2构成互质关系，比如17和15。

3.RSA算法的过程

• 1. 寻找两个不相同的大质数p，q
  这两个质数越大，就越难破解。
  如：p=17,q=29

• 2.计算n=pq。
  n的二进制表示时所占用的位数，就是所谓的密钥长度。
  如：n=pq=493,493写成二进制是111101101，一共有9位，所以这个密钥长度就是9位。实际应用中，RSA密钥一般是1024位，重要场合则为2048位。

• 3.计算r:r=(p-1)(q-1)
  如：r=(p-1)(q-1)=448

• 4.随机选择一个小于r并与r互质的奇整数e
  如：选择e=5

• 5.计算d:d是e关于r的模反元素。
  所谓"模反元素"就是指有一个整数d，可以使得ed被r除的余数为1。即ed mod r =1.
  如：d=269。
  ed=5*269=1345,and ed%448=1

• 6.将e和n封装成公钥P=(e,n)
  如：P=（5,493)

• 7.将d和n封装成密钥S=(d,n)
  如：S=（269，493）

• 8.定义函数$F_p$与$F_s$
  $F_p(x)=x^{e}mod$ n
  $F_s(x)=x^{d}mod$ n

总结，实际上就是计算n,e,d的过程。

4.python RSA加解密

python3 可以使用 Crypto.PublicKey.RSA 和 rsa 生成公钥、私钥。
rsa 加解密的库使用 pip install rsa 就行了

import rsa# rsa加密def rsaEncrypt(str):#str:加密的文本    # 生成公钥、私钥    (pubkey, privkey) = rsa.newkeys(512)    print("公钥:\n%s\n私钥:\n:%s" % (pubkey, privkey))    # 明文编码格式    content = str.encode("utf-8")    # 公钥加密    crypto = rsa.encrypt(content, pubkey)    return (crypto, privkey)  # rsa解密def rsaDecrypt(str, pk):    # 私钥解密    content = rsa.decrypt(str, pk)    con = content.decode("utf-8")    return con  if __name__ == "__main__":     str, pk = rsaEncrypt("hello，world")    print("加密后密文：\n%s" % str)    content = rsaDecrypt(str, pk)    print("解密后明文：\n%s" % content)

8.5利用cryptography 进行加密和解密

from cryptography.fernet import Fernet#生成秘钥cipher_keycipher_key = Fernet.generate_key()print(cipher_key)cipher = Fernet(cipher_key)text = b'My name is PanChao.'#进行加密encrypted_text = cipher.encrypt(text)print(encrypted_text)#进行解密decrypted_text = cipher.decrypt(encrypted_text)print(decrypted_text)

9 Data Compression

数据压缩
Q: Why would we want to compress information？
A: to save time and space
Q: What is the quality of the compressed information?
A：lossless compression and lossy compression（无损压缩和有损压缩）
Q： Why is it possible to compress information?
A：

• for lossy compression:you just tolerate how the precision decreases.
• for lossless compression:Digital information often contains redundant （冗余的）or useless （无用的）bits

9.1Huffman codes（霍夫曼编码）

霍夫曼编码又称之为哈夫曼编码,无损压缩的一种。
prefix-free code(无前缀代码)
The code for A is 0, and no other code starts with 0; the code for T is 11, and no other code starts with 11; and so on. We call such a code a prefix-free code。
A的代码是0，没有其他代码以0开头；T的代码是11，没有其他代码以11开头；依此类推。我们称这种代码为无前缀代码。
通讯领域中常用的编码方式
1.定长编码
对原始数据不加任何的修改，按照对应的编码集，转成二进制代码进行存储。占用空间大。
2.变长编码

• 按照字符出现的频率进行编码，原则上频率越高，其编码长度越小。如出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码。。
• 是比较简洁，但是会出现多义性，因为代码彼此之间有重复。
• 无前缀编码：字符的编码不是其余字符编码的前缀。

霍夫曼树(哈夫曼树）

• 霍夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。
• 路径： 树中一个结点到另一个结点之间的分支构成这两个结点之间的路径。
• 路径长度：路径上的分枝数目称作路径长度。
• 树的路径长度：从树根到每一个结点的路径长度之和。
• 权值：就是定义的路径上面的值。可以这样理解为节点间的距离。通常指字符对应的二进制编码出现的概率。至于霍夫曼树中的权值可以理解为：权值大表明出现概率大！
• 树的带权路径长度(WPL)，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1L1+W2L2+W3L3+…+WnLn），N个权值Wi（i=1,2,…n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,…n）。可以证明霍夫曼树的WPL是最小的。
  
  上面三个二叉树的带权路径长度分别为：
  (1)$WPL=7\ast 2+5\ast 2+2\ast 2+4\ast 2=36$
  (2)$WPL=4\ast 2+7\ast 3+5\ast 3+2\ast 1=46$
  (3)$WPL=7\ast 1+5\ast 2+2\ast 3+4\ast 3=35$
  通过上面三个二叉树的WPL分析知一棵二叉树要使其WPL值最小，必须使权值越大的叶子结点越靠近根结点，而权值越小的叶子结点越远离根结点。

霍夫曼树的构造
基本思想

例子：

伪代码：


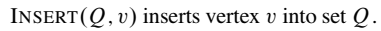
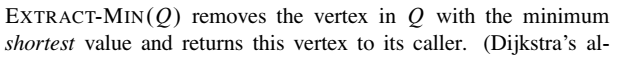
python：

def Build_Huffman_Tree(char,freq,n):    Q=[]    for i in range(n):        z=[]        z.append(char[i])        z.append(freq[i])        Q.append(z)     for _ in range(n-1):        Q=sorted(Q,key=lambda x:x[1])        x=EXTRACT_MIN(Q)        Q.remove(Q[0])        Q=sorted(Q,key=lambda x:x[1])        y=EXTRACT_MIN(Q)        Q.remove(Q[0])        z=[x[0]+y[0],x[1]+y[1]]        INSERT(Q,z)        print(Q)    return EXTRACT_MIN(Q)[1]def EXTRACT_MIN(Q):    x=Q[0]    return xdef INSERT(Q,z):    Q.append(z)    return Q

霍夫曼编码(Huffman Codes)
通过霍夫曼树来构造的编码称为哈弗曼编码（huffman code）。

• 霍夫曼编码是一种编码方法，属于一种程序算法。
• 霍夫曼编码是 可变字长编码(VLC) 的一种，由霍夫曼提出，又称之为最佳编码。在计算机数据处理中，霍夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码。
• 霍夫曼编码是霍夫曼树在通讯领域的经典应用之一。
• 霍夫曼编码广泛用于数据文件的压缩，压缩率通常在20% 到90%，通常数据的重复率越高，那么压缩率就越高。

霍夫曼编码(Huffman Codes)的基本步骤：

• 利用字符集中每个字符的使用频率作为权值构造一个哈夫曼树；
• 从根结点开始，为到每个叶子结点路径上的左分支赋予0，右分支赋予1，并从根到叶子方向形成该叶子结点的编码。

9.2 LZW compression

LZW和哈夫曼编码一样，是无损压缩中的一种。该算法通过建立字典，实现字符重用与编码，适用于source中重复率很高的文本压缩。

ASCII 字符代码表

9.2.1 LZW compressor

LZW压缩基本原理：
提取原始文本文件数据中的不同字符，基于这些字符创建一个编码表，然后用编码表中的字符的索引来替代原始文本文件数据中的相应字符，减少原始数据大小。
核心思想：利用字符的可重用性，每当往结果输出一个编码，就将一个新的string存入dictionary
编码：
对于文本来说，依次往后读取每一个字符。

• 编码0～255是固定的，用来存储Ascii码为[0,255]的字符，放在字典里。
• 编码从256开始，每次读入一个字符，如果发现和前缀加起来在字典中不存在，那么就建立码表，并输出前缀的值，将后读取的字符赋给前缀；如果存在就将前缀和后缀一起赋给前缀，继续读取下一个字符给后缀，如此往复。直到读取完整个字符串。

例子：压缩文本 TATAGATCTTAATATA

伪代码：

python：

#LZW编码def lzw_compressor(text):    dictionary={   chr(i):i for i in range(1,123)}#chr(i) 返回整数i对应的ASCII字符    last=256#从256开始建立新的编码    result=[]    s=''    while s == '':        for c in text:            sc=s+c            if sc in dictionary:                s=sc            else:                result.append(dictionary[s])                dictionary[sc]=last                last+=1                s=c    result.append(dictionary[s])    return resulttext = "TAGTA" lzw_compressor(text)

9.2.2 LZW decompressor

lZW解压即译码，核心思想在于解码需要还原出编码时的用的字典，然后一边读取一边解码，然后扩充码表。
译码：

1. 初始状态，字典里只有所有的默认项，例如0->a，1->b，2->c。此时pW和cW都是空的。
2. 读入第一个的符号cW，解码输出。注意第一个cW肯定是能直接解码的，而且一定是单个字符。
3. 赋值pW=cW。
4. 读入下一个符号cW。
5. 在字典里查找cW，如果:
   a. cW在字典里：
   (1) 解码cW，即输出 Str(cW)。
   (2) 令P=Str(pW)，C=Str(cW)的第一个字符。
   (3) 在字典中为P+C添加新的记号映射。
   b. cW不在字典里:
   (1) 令P=Str(pW)，C=Str(pW)的第一个字符。
   (2) 在字典中为P+C添加新的记号映射，这个新的记号一定就是cW。
   (3) 输出P+C。
6. 返回步骤3重复，直至读完所有记号。
   伪代码：
   
   python：

#LZW译码def lzw_decompressor(indices):    dictionary = {   i:chr(i) for i in range(1,123)}    last = 256    result = []    s = arr.pop(0)#pop(i)移除列表中第i个元素    result.append(dictionary[s])    for c in indices:        if c in dictionary:            entry = dictionary[c]        result.append(entry)        dictionary[last] = dictionary[s] + entry[0]        last += 1        s = c    print(''.join(result))indices = [84, 65, 256, 71, 257, 67, 84, 256, 257, 264]lzw_decompressor(indices)

可以将编码，译码结合起来，计算压缩比。

string =input('请输入需要压缩的字符串：')a=lzw_compressor(stringb=lzw_decompressor(a)print('压缩后的编码:'a)print('解压后的译码:'b)n1=len(string)#计算原字符串长度n2=len(a)#计算编码长度X=(n2*9)/(n1*8)#计算压缩比print('LZW的压缩比:'X)

10 Hard? Problems

10.1The classes P and NP and NP-completeness

• P:P类问题就是在多项式时间内可以解决的问题。

• NP:NP类问题就是指那些在多项式时间内可以被证明的问题。所有的P类问题同时也是NP问题。

• NP-hard:一个问题，如果有一个多项式时间算法可以解决该问题，那么我们可以将NP中的每个问题转换为该问题，从而以多项式时间解决NP中的每一个问题。

• NP-complete:如果一个问题既是NP问题又是NP-hard问题，则它是NP完全的。准确的来说，如果对于这些问题来说，有一个多项式时间O($n^c$)运行的算法，其中c是一个常数，那么对于所有的问题，都将以O($n^c$)时间运行，称这些问题为NP完全。
  例子：一个连通的，无向的图是否有哈密顿圈，这就是一个NP完全问题。

证明NP完全问题，依赖与以下几个方面：

1.决定问题：回答“是”或“否”的问题称为决定问题
2.最优化问题均可以转换为决定问题。
3.减少：如果Y有多项式时间算法，那么X就有多项式时间算法。我们称这种转换为减少，因为我们正在将解决问题X“减少”到解决问题Y。
如果问题X是NP-hard的，我们可以在
多项式时间内将其减少到问题Y，那么问题Y也是NP-hard的。

10.2 NP-complete

Hamiltonian cycle and hamiltonian path

1.哈密顿回路问题：一个连通的无向图是否包含一个哈密顿回路（一条路径在同一顶点处开始和结束，并访问所有其他顶点一次）？

-存在哈密顿回路的图就是哈密顿图.哈密顿图就是从一点出发,经过除起点所有的顶点必须且只能一次,最终回到起点的路径.图中有的边可以不经过,但是不会有边被经过两次.

• 证明:需要检查每个顶点在列表中是否恰好出现一次，并且该图形在顺序中每对连续的顶点之间是否都包含一条边，第一个顶点与最后一个顶点之间是否存在一条边。

• 哈密顿回路问题是NP完全问题。

2.哈密顿路径问题：询问连通的无向图图是否包含一次访问每个顶点的路径，但不要求该路径为闭合循环。

• 证明:需要检查每个顶点在列表中是否恰好出现一次，并且该图形在顺序中每对连续的顶点之间是否都包含一条边。
• 哈密顿路径问题是NP完全问题。

3.将哈密顿回路问题化简为哈密顿路径问题，如果证明哈密顿路径问题是NP完全问题，则哈密顿回路问题也是NP完全问题

10.3最短Hamilton路径

问题概要：
给定一张 n个点的带权无向图，点从0∼n−1标号，求起点 0 到终点 n-1 的最短Hamilton路径。Hamilton路径的定义是从 0 到 n-1 不重不漏地经过每个点恰好一次。

思路分析：
输入：

• 一个整数n,表示最短路径的长度
• 邻接矩阵表示距离矩阵，其中第i行第j个整数表示点i到j的距离

输出：遍历点过程

过程：

• Hamilton路径需要0 到 n-1 每个点恰好一次经过，因此我们将一次经过设置成一个0或1的状态：0表示未经过，1表示经过
• 由于路径最短，那么要求子路径也最短+距离最小值，根据两个条件确定使用动态规划解题。

python：

"""halmilton question"""__revision__ = '0.1'def isOK(k,x,c):    for i in range (0,k):        if x[k]==x[i] or not c[x[k]][x[k-1]]:            return 0    return 1def hamilton(n, x, c):    for i in range(0,n):        x[0]=i        k=1        while k>0:            while k<n and x[k]<n and not isOK(k,x,c):                 x[k]=x[k]+1            if x[k]<n:                if k==n-1:                    if c[x[0]][x[k]]:                        print("%d,%d,%d,%d,%d" % (x[0],x[1],x[2],x[3],x[4]))                    k=k-1                    x[k]=x[k]+1                else:                    k=k+1                    x[k]=0            else:                k=k-1                x[k]=x[k]+1if __name__=="__main__":    c=[ [0,1,0,1,0],        [1,0,1,1,1],        [0,1,0,1,1],        [1,1,1,0,1],        [0,1,1,1,0] ]    x=[0,0,0,0,0]    n=5    hamilton(n,x,c)# zou@ICT-FFC822E11FE:~/Code/algorithm$ python hamilton.py# 0,1,2,4,3# 0,1,4,2,3# 0,3,2,4,1# 0,3,4,2,1

参考资料：
https://blog.csdn.net/qq_41137136/article/details/86433998