本文共 5516 字，大约阅读时间需要 18 分钟。

Lasso概念

• 定义

LASSO是由1996年Robert Tibshirani首次提出，全称Least absolute shrinkage and selection operator。该方法是一种压缩估计。它通过构造一个惩罚函数得到一个较为精炼的模型，使得它压缩一些回归系数，即强制系数绝对值之和小于某个固定值；同时设定一些回归系数为零。因此保留了子集收缩的优点，是一种处理具有复共线性数据的有偏估计。

除了岭回归之外,最常被人们提到就是模型 Lasso。和岭回归一样,Lasso来作用于多重共线性问题的算法,不过 Lasso使用的是系数w的L1范式(L1范式则是系数w的绝对值)乘以系数α,所以 Lasso的损失函数表达式为:

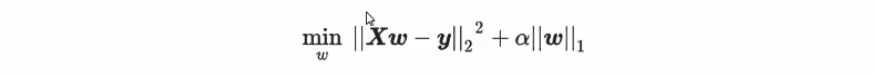
• Lasso处理多重共线性原理

一般来说, Lasso与岭回归非常相似,都是利用正则项来对原本的损失函数形成一个惩罚,以此来防止多重共线性。但是其实这种说法不是非常严谨,我们来看看 Lasso的数学过程。当我们使用最小二乘法来求解 Lasso中的参数w,我们依然对损失函数进行求导:

所有这些让 Lasso成为了一个神奇的算法,尽管它是为了限制多重共线性被创造出来的,然而大部分地方并不使用它来抑制多重共线性,反而接受了它在其他方面的优势。在逻辑回归中涉及到，L1和L2正则化一个核心差异就是他们对系数w的影响:两个正则化都会压缩系数w的大小,对标签贡献更少的特征的系数会更小,也会更容易被压缩。不过,L2正则化只会将系数压缩到尽量接近0,但L1正则化主导稀疏性,因此会将系数压缩到0。这个性质,让 Lasso成为了线性模型中的特征选择工具首选,接下来,我们就来看看如何使用 Lasso来选择特征。

二、linear_model.Lasso 类

class sklearn.linear_model.Lasso(alpha=1.0, *, fit_intercept=True, normalize=False, precompute=False,                                  copy_X=True, max_iter=1000, tol=0.0001, warm_start=False,                                  positive=False, random_state=None, selection='cyclic')[source]

sklearn中我们使用Lasso类来调用lasso回归,众多参数中我们需要比较在意的就是参数α,正则化系数。要注意的就是参数 positive.当这个参数为True的时候,我们要求 Lasso回归处的系数必须为正数,以此证我们的α一定以增大来控制正则化的程度。

在skLearn中的Lasso使用的损失函数是：

案例：Lasso特征选取

① 读取数据集

# -*- coding: utf-8#  @Time    : 2021/1/15 15:14#  @Author  : ZYX#  @File    : Example6_Lasso.py# @software: PyCharmimport numpy as npimport pandas as pdfrom matplotlib import pyplot as pltfrom sklearn.linear_model import Lasso,Ridge,LinearRegressionfrom sklearn.model_selection import train_test_split,cross_val_scorefrom sklearn.datasets import fetch_california_housing as fch# 获取数据集house_value = fch()x = pd.DataFrame(house_value.data)y = house_value.targetx.columns = ["住户收入中位数","房屋使用年代中位数","平均房间数目","平均卧室数目","街区人口","平均入住率","街区的纬度","街区的经度"]

② 划分训练集、测试集

# 划分测试集和训练集xtrain,xtest,ytrain,ytest = train_test_split(x,y,test_size=0.3,random_state=420)# 重置索引for i in [xtrain,xtest]:    i.index = range(i.shape[0])

③ 对线性回归、岭回归、Lasso进行对比

# 线性回归进行拟合reg = LinearRegression().fit(xtrain,ytrain)reg_list = (reg.coef_*100).tolist()#[43.73589305968403, 1.0211268294494038, -10.780721617317715, 62.64338275363783, 5.216125353178735e-05, -0.33485096463336095, -41.30959378947711, -42.621095362084674]# 岭回归进行拟合Ridge_ = Ridge(alpha=0).fit(xtrain,ytrain)Ridge_list = (Ridge_.coef_*100).tolist()#[43.735893059684045, 1.0211268294494151, -10.780721617317626, 62.64338275363741, 5.2161253532713044e-05, -0.3348509646333588, -41.3095937894767, -42.62109536208427]# Lasso进行拟合Lasso_ = Lasso(alpha=0).fit(xtrain,ytrain)Lasso_list = (Lasso_.coef_*100).tolist()#[43.735893059684045, 1.0211268294494151, -10.780721617317626, 62.64338275363741, 5.2161253532713044e-05, -0.3348509646333588, -41.3095937894767, -42.62109536208427]

我们可以看出，当岭回归和Lasso中的alpha都设定为0的时候，拟合的w都几乎差不了多少。但是Lasso尽管运行除了结果，却报了三个UserWarning：

UserWarning: With alpha=0, this algorithm does not converge well. You are advised to use the LinearRegression estimator  Lasso_ = Lasso(alpha=0).fit(xtrain,ytrain)UserWarning: Coordinate descent with no regularization may lead to unexpected results and is discouraged.  positive)ConvergenceWarning: Objective did not converge. You might want to increase the number of iterations. Duality gap: 3769.8607714139102, tolerance: 1.917255476913148  positive)

这三条分别是这样的内容:

• 1.正则化系数为0,这样算法不可收敛!如果你想让正则化系数为0,请使用线性回归吧
• 2.没有正则项的坐标下降法可能会导致意外的结果,不鼓励这样做!
• 3.目标函数没有收敛,你也许想要增加迭代次数,使用一个非常小的 alpha来拟合模型可能会造成精确度问题!

看到这三条内容,大家可能会难以理解 ---- 怎么出现了坐标下降?这是由于 sklearn中的Lasso类不是使用最小二乘法来进行求解,而是使用坐标下降。考虑一下 Lasso既然不能够从根本解决多重共线性引起的最小二乘法无法使用的问题,那我们为什么要坚持最小二乘法呢?明明有其他更快更好的求解方法,比如。

有了坐标下降,就有迭代和收敛的问题,因此 sklearn不推荐我们使用0这样的正则化系数。如果我们的确希望取到0,那我们可以使用一个比较很小的数,比如0.01,或者10*e-3这样的值:

# 更改alpha# 岭回归进行拟合Ridge_ = Ridge(alpha=0.01).fit(xtrain,ytrain)Ridge_list1 = (Ridge_.coef_*100).tolist()#[43.73575720621605, 1.0211292318121836, -10.780460336251702, 62.64202320775686, 5.217068073243689e-05,# -0.3348506517067627, -41.3095714322911, -42.62105388932374]# Lasso进行拟合Lasso_ = Lasso(alpha=0.01).fit(xtrain,ytrain)Lasso_list1 = (Lasso_.coef_*100).tolist()# [40.10568371834486, 1.0936292607860143, -3.7423763610244487, 26.524037834897207, # 0.0003525368511503945, -0.3207129394887799, -40.06483047344844, -40.81754399163315]

[43.73589305968403, 1.0211268294494038, -10.780721617317715, 62.64338275363783, 5.216125353178735e-05,  -0.33485096463336095, -41.30959378947711, -42.621095362084674]

通过对比可以发现，Lasso相对于岭回归而言，对于alpha的变化十分敏感。

假设我们对alpha再进行更改：

# 岭回归进行拟合Ridge_ = Ridge(alpha=10**4).fit(xtrain,ytrain)Ridge_list2 = (Ridge_.coef_*100).tolist()#[34.620815176076945, 1.5196170869238694, 0.3968610529210133, 0.9151812510354866, 0.002173923801224843, # -0.34768660148101016, -14.736963474215257, -13.43557610252691]# Lasso进行拟合Lasso_ = Lasso(alpha=10**4).fit(xtrain,ytrain)Lasso_list2 = (Lasso_.coef_*100).tolist()# [0.0, 0.0, 0.0, -0.0, -0.0, -0.0, -0.0, -0.0]

将alpha扩大至10000的时候，可以发现岭回归和Lasso的结果完全不同，岭回归仅有部分特征被压缩至趋近于0，而Lasso的所有特征全部压缩至了等于0,由此再次可以说明Lasso对于alpha的敏感。

④ 学习曲线

reg = LinearRegression().fit(xtrain,ytrain)Ridge_ = Ridge(alpha=10**4).fit(xtrain,ytrain)Lasso_ = Lasso(alpha=1).fit(xtrain,ytrain)# 绘制学习曲线plt.plot(range(1,9),(reg.coef_*100).tolist(),color='red',label='LR')plt.plot(range(1,9),(Ridge_.coef_*100).tolist(),color='green',label='Ridge')plt.plot(range(1,9),(Lasso_.coef_*100).tolist(),color='black',label='Lasso')plt.plot(range(1,9),[0]*8,color='grey',linestyle='--')plt.xlabel('w')plt.legend()plt.show()

通过图像可以看出，通过Lasso可以将特征系数压缩为0，而岭回归可以将特征系数压缩的无限逼近于0。可见,比起岭回归, Lasso所带的L1正则项对于系数的惩罚要重得多,并且它会将系数压至0，可以被用来做特征选择。也因此,我们往往让 Lasso正则化系数a在很小的空间中变动,以此来寻找最佳的正则化系数。