本文共 1169 字，大约阅读时间需要 3 分钟。

Description

学校有n台计算机，为了方便数据传输，现要将它们用数据线连接起来。两台计算机被连接是指它们之间有数据线连接。由于计算机所处的位置不同，因此不同的两台计算机的连接费用往往是不同的。
当然，如果将任意两台计算机都用数据线连接，费用将是相当庞大的。为了节省费用，我们采用数据的间接传输手段，即一台计算机可以间接的通过若干台计算机（作为中转）来实现与另一台计算机的连接。
现在由你负责连接这些计算机，你的任务是使任意两台计算机都连通（不管是直接的或间接的）。

Input

输入文件wire.in，第一行为整数n（2<=n<=100），表示计算机的数目。此后的n行，每行n个整数。第x+1行y列的整数表示直接连接第x台计算机和第y台计算机的费用。

Output

输出文件wire.out，一个整数，表示最小的连接费用。

Sample Input

3
0 1 2
1 0 1
2 1 0

Sample Output

2（注：表示连接1和2，2和3，费用为2）

解题思路

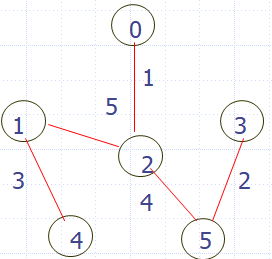
很明显的最小生成树模板

kruskal算法
每次找最小的边，如果边连接的两个点不是一个集合的，那么就把这两个点连起来

不断找最短的边，并且这条边的两个点不在一个集合里

最后

顺便推一下

#include<iostream>#include<cstdio>using namespace std;const int INF=0x7fffffff;int a[200][200],n,p[200],Gun;void kruskal(){   	for(int g=1;g<n;g++){   //因为必定只会连n-1条边		int mi=INF,k,l;		for(int i=1;i<=n;i++)		    for(int j=1;j<=n;j++)		        if(a[i][j]<mi&&a[i][j]&&p[i]!=p[j]){   //两点不在一个集合p[i]!=p[j]		        	mi=a[i][j];		        	k=i,l=j;		        }	    Gun+=a[k][l]; //累计答案	    int s=p[k];		for(int i=1;i<=n;i++)		    if(p[i]==s)//因为总有一个i==k,把p[k]赋成p[l],后面都赋值不了了		       p[i]=p[l];	}}int main(){   	scanf("%d",&n);	for(int i=1;i<=n;i++){   		p[i]=i;		for(int j=1;j<=n;j++)		    scanf("%d",&a[i][j]);	}	kruskal();	printf("%d",Gun);}