
本文共 6358 字,大约阅读时间需要 21 分钟。
目录
leetcode 455
你想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。对每个孩子 i ,都有一个胃口值 gi ,这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j ,都有一个尺寸 sj 。如果 sj >= gi ,我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
注意:
你可以假设胃口值为正。一个小朋友最多只能拥有一块饼干。
示例 1:
输入: [1,2,3], [1,1]输出: 1解释: 你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。所以你应该输出1。
示例 2:
输入: [1,2], [1,2,3]输出: 2解释: 你有两个孩子和三块小饼干,2个孩子的胃口值分别是1,2。你拥有的饼干数量和尺寸都足以让所有孩子满足。所以你应该输出2.
思路
先排序,然后从后往前依次对比。
- 如果糖果能满足孩子,则继续向前对比;
- 如果糖果不能满足孩子,则孩子继续向前因为排序之后孩子的g值是从小到大排列的,当前糖果满足不了当前的孩子,但是也许可以满足前一个孩子)。
- 当糖果的索引值小于0或者孩子的索引值小于0时,对比结束,输出累计的所有满足条件(g<=s)的成果。

class Solution {public: int findContentChildren(vector & g, vector & s) { //胃口是g,冰棍是s if(g.empty()|| s.empty()) return 0; sort(g.begin(),g.end()); sort(s.begin(),s.end()); int res=0, index=s.size()-1; for(int i=g.size()-1;i>=0;){ if(index>=0){ if(g[i]<=s[index]){ res++; index--; } i--; }else{ break; } } return res; }}; 
leetcode 376 ——划分状态的思想
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为摆动序列。第一个差(如果存在的话)可能是正数或负数。少于两个元素的序列也是摆动序列。
例如, [1,7,4,9,2,5] 是一个摆动序列,因为差值 (6,-3,5,-7,3) 是正负交替出现的。相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
给定一个整数序列,返回作为摆动序列的最长子序列的长度。 通过从原始序列中删除一些(也可以不删除)元素来获得子序列,剩下的元素保持其原始顺序。
示例 1:
输入: [1,7,4,9,2,5]输出: 6 解释: 整个序列均为摆动序列。
示例 2:
输入: [1,17,5,10,13,15,10,5,16,8]输出: 7解释: 这个序列包含几个长度为 7 摆动序列,其中一个可为[1,17,10,13,10,16,8]。
示例 3:
输入: [1,2,3,4,5,6,7,8,9]输出: 2
进阶:
你能否用 O(n) 时间复杂度完成此题? 能!!!思考:
用贪心算法,如果出现两个连续的同符差值,差值为负则证明此段输入序列是三个递增的数,去掉中间的那个数,差值为正则证明此段序列是三个递减数,则去掉中间的数。如此,如果按例题2中的输入序列,最终保留的输出序列应为[1,17,5,15,5,16,8],与例子1给出的输出序列不一致,但是结果是对的。而且可以保证是O(n)。



class Solution {public: int wiggleMaxLength(vector & nums) { int len=nums.size(); if(len<2) return len; static const int BEGIN=0; static const int UP=1; static const int DOWN=2; int state=BEGIN; int max_len=1; for(int i=1;i nums[i-1]){ state=UP; max_len++; } else if(nums[i] nums[i-1]){ state=UP; max_len++; } break; } } return max_len; }}; 
leetcode 402 ——主要考察细节处理
给定一个以字符串表示的非负整数 num,移除这个数中的 k 位数字,使得剩下的数字最小。
注意:
- num 的长度小于 10002 且 ≥ k。
- num 不会包含任何前导零。
示例 1 :
输入: num = "1432219", k = 3输出: "1219"解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。
示例 2 :
输入: num = "10200", k = 1输出: "200"解释: 移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。
示例 3 :
输入: num = "10", k = 2输出: "0"解释: 从原数字移除所有的数字,剩余为空就是0。
思考


边界条件:

思路:
要确保较高位比较低位的值小。则利用栈:
将字符串中字符依次入栈,如果当前字符串比栈顶元素小,并且还可以继续删除元素,那么就将栈顶元素删掉,这样会得到最小数字序列。
class Solution {public: string removeKdigits(string num, int k) { vector S; string result=""; for(int i=0; i number && k>0){ S.pop_back(); k--; } if(number || S.size()){ S.push_back(number); } } //k不等于0,说明还可以继续删除元素 while(k && S.size()){ S.pop_back(); k--; } for(int i=0; i 
leetcode 55 ——就是一直考虑我还能不能再跳
给定一个非负整数数组,你最初位于数组的第一个位置。数组中的每个元素代表你在该位置可以跳跃的最大长度。判断你是否能够到达最后一个位置。
示例 1:
输入: [2,3,1,1,4]输出: true解释: 从位置 0 到 1 跳 1 步, 然后跳 3 步到达最后一个位置。
示例 2:
输入: [3,2,1,0,4]输出: false解释: 无论怎样,你总会到达索引为 3 的位置。但该位置的最大跳跃长度是 0 , 所以你永远不可能到达最后一个位置。
思路:
问能不能跳到数组的末尾位置,那就分别在数组的每个位置时所能跳到的最远位置。如果当前数组的位置超过了之前索引位置所能到达的最远位置,则说明跳不到。
比如说,[1, 0, 1] ,数组每个位置所能跳到的最远位置为[1, 1, x], 由于第二个索引位置所能到达的最远位置为 1, 因为无法到达数组索引位置为2的位置,并且索引位置为 1 之前的所有元素所能到达的最远距离都没有能到达位置为 2 的,因此,该数组无法到达数组的末尾。
不断更新能到达的最远位置,如果当前索引位置的值超出了所能到达的最远位置,则说明无法跳到当前索引位置,就更别提能跳到数组末尾了。所能到达的最远位置如果都超过数组的末尾了,那么就肯定能到达数组的末尾了。
class Solution {public: bool canJump(vector & nums) { if(nums.empty()) return true; int jump=0; int max_length=nums[0]; vector index; //记录每一步可以跳到的最远的地方 for(int i=0; i 
leetcode 45 ——考虑跳的步数最少
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
示例:
输入: [2,3,1,1,4]输出: 2解释: 跳到最后一个位置的最小跳跃数是 2。 从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
思路:
使用两个变量,一个记录当前所能到达的最远距离,一个记录未来所能到达的最远距离。
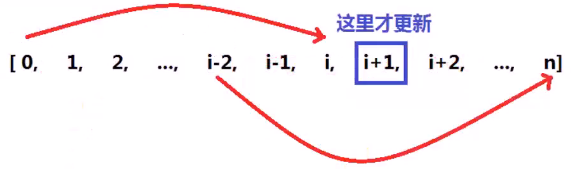
设定跳跃步数的初始值为1,,设定当前所能到达的最远距离的初始值为数组第0索引位置的值,之后依次计算未超过当前所能到达的最远距离的每一个位置所能到达的最远距离,记录这些距离中最远的当做未来所能到达的最远距离。
当当前到达的索引位置超过了当前所能到达的最远距离时,跳跃步数加一,更新当前所能到达的最远距离的值为未来所能到达的最远距离(即上图中num[0]=i ,设置 i 为,当前所能到达的最远距离, 不断计算0到 i 之间每一步所能跳的最远的地方,当遍历到 i+1 时,说明此时不得不跳了,选择位置 i-2 的那里作为起跳点,因为那里所能到达的位置最远)
class Solution {public: int jump(vector & nums) { //数组尺寸小于2,不用跳了 if(nums.size()<2) return 0; //当前所能到达的最远位置 int current_max_index=nums[0]; //未来所能到达的最远位置 int future_max_index=nums[0]; //跳跃步数 int jump_min=1; for(int i=0; i current_max_index){ jump_min++; current_max_index=future_max_index; } if(future_max_index 
leetcode 452
在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以y坐标并不重要,因此只要知道开始和结束的x坐标就足够了。开始坐标总是小于结束坐标。平面内最多存在104个气球。
一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
Example:
输入:[[10,16], [2,8], [1,6], [7,12]]输出:2解释:对于该样例,我们可以在x = 6(射爆[2,8],[1,6]两个气球)和 x = 11(射爆另外两个气球)。

思路:


下面的代码不给sort传比较方法cmp其实也可以,我留着,是为了多记录一下。
static const auto init = []() { std::ios::sync_with_stdio(false); std::cin.tie(nullptr); return nullptr;}();bool cmp(const pair &a, const pair &b){ return a.first >& points) { if(points.empty()) return 0; //按照气球第一个元素排序 sort(points.begin(),points.end(),cmp); int shoot_num=1; int shoot_begin=points[0].first; int shoot_end=points[0].second; for(int i=1; i points[i].second){ shoot_end=points[i].second; } //说明当前气球无法和之前的气球一起打 }else{ shoot_num++; shoot_begin=points[i].first; shoot_end=points[i].second; } } return shoot_num; }}; 
发表评论
最新留言
关于作者
