目录:
1、冒泡排序(Bubble Sort)
2、选择排序(Selection Sort)
3、插入排序(Insertion Sort)
4、希尔排序(Shell Sort)
5、归并排序(Merge Sort)
6、快速排序(Quick Sort)
7、堆排序(Heap Sort)
8、计数排序(Counting Sort)
9、桶排序(Bucket Sort)
10、基数排序(Radix Sort)
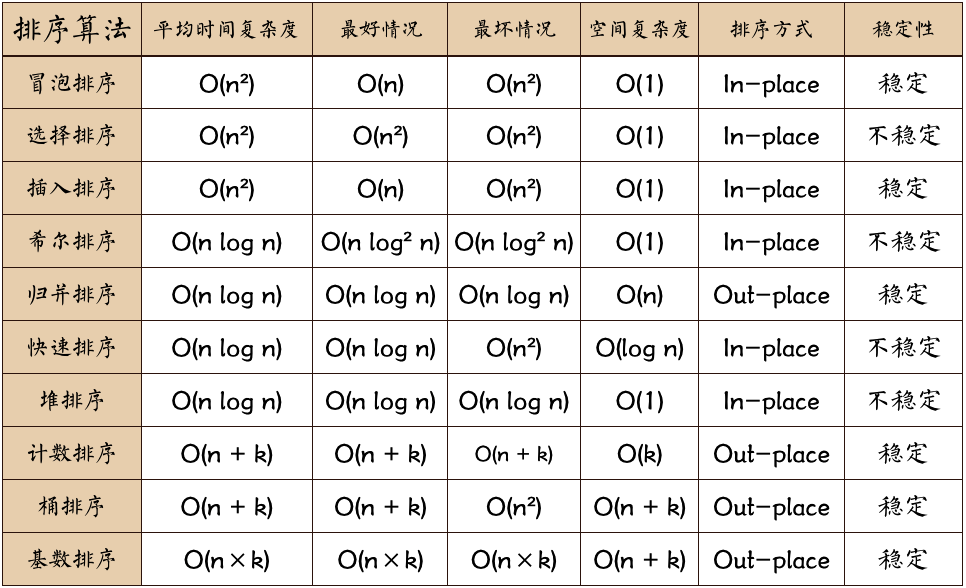
1、冒泡排序(Bubble Sort)
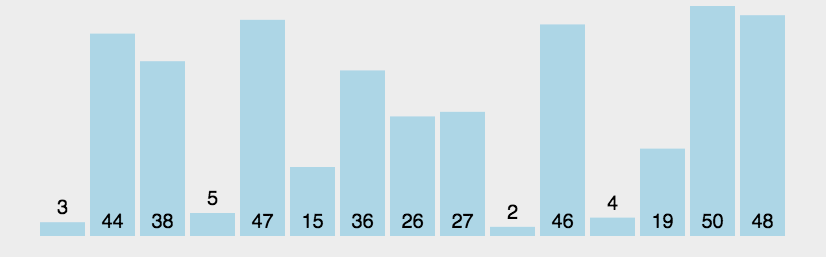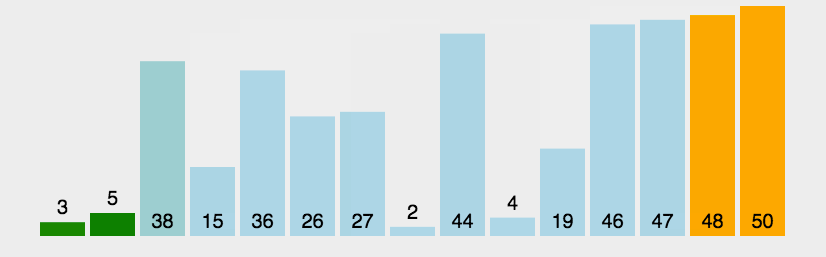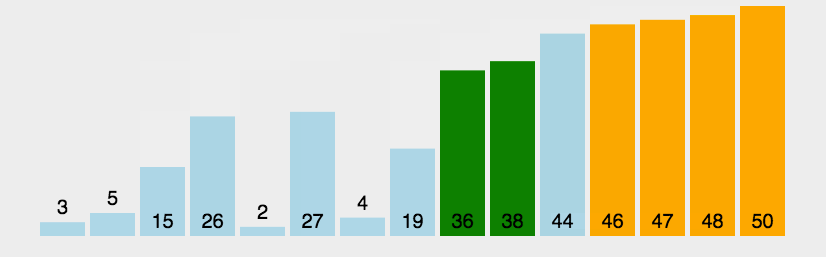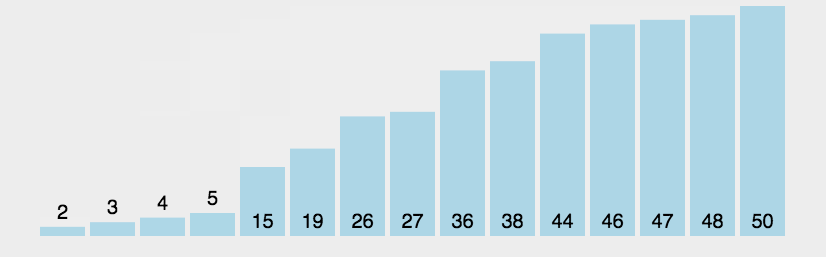
1、基本思想:两个数比较大小,较大的数下沉,较小的数冒起来。
2、算法描述:
比较相邻的元素。如果第一个比第二个大,就交换它们两个;
对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;针对所有的元素重复以上的步骤,除了最后一个;重复步骤1~3,直到排序完成。3、实现列子:public static void main(String[] args) {
int [] array={1,20,11,90,50,2000,39}; int steam; boolean flase; for(int i=0;i<array.length-1;i++){ flase=false; for (int j=array.length-1; j>i; j--) { if(array[j]<array[j-1]){ steam=array[j]; array[j]=array[j-1]; array[j-1]=steam; flase=true; } } if(!flase) break; } System.out.println(Arrays.toString(array)); }2、选择排序(Selection Sort)
1、动态图
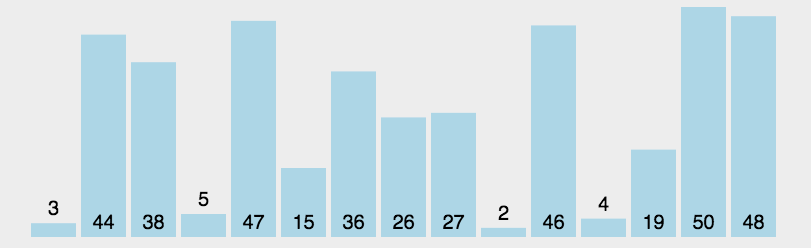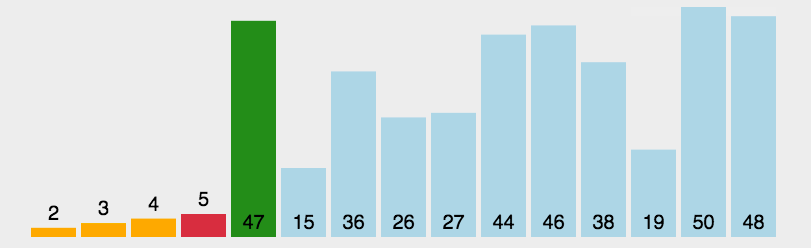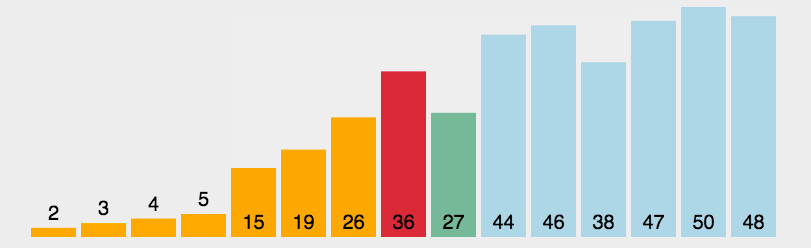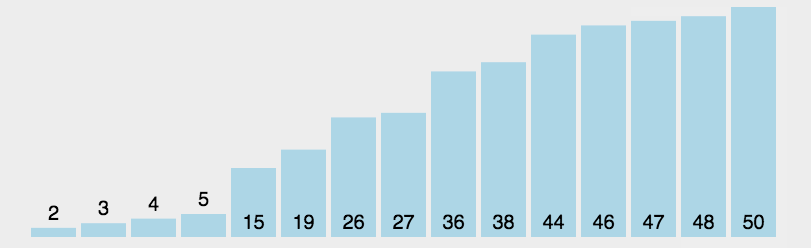
2、
表现最稳定的排序算法之一,因为无论什么数据进去都是O(n2)的时间复杂度,所以用到它的时候,数据规模越小越好。唯一的好处可能就是不占用额外的内存空间了吧。理论上讲,选择排序可能也是平时排序一般人想到的最多的排序方法了吧。
选择排序(Selection-sort)是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
2.1 算法描述
n个记录的直接选择排序可经过n-1趟直接选择排序得到有序结果。具体算法描述如下:
- 初始状态:无序区为R[1..n],有序区为空;
- 第i趟排序(i=1,2,3…n-1)开始时,当前有序区和无序区分别为R[1..i-1]和R(i..n)。该趟排序从当前无序区中-选出关键字最小的记录 R[k],将它与无序区的第1个记录R交换,使R[1..i]和R[i+1..n)分别变为记录个数增加1个的新有序区和记录个数减少1个的新无序区;
- n-1趟结束,数组有序化了。
3、实现列子:
public static void main(String[] args) {
int[] array = { 11, 1, 22, 33, 55, 44, 3 }; for (int i = 0; i < array.length; i++) { //加入获取的第一个数字就是最小的开始与第二个数字进行比较 int min = i;for (int j = i + 1; j < array.length; j++) {//从第二个数字开始往后循环比较
if (array[j] < array[min]) { min = j; } } SelectionSort.swap(array, i,min); } System.out.println(Arrays.toString(array)); }private static void swap(int[] arr, int i, int j) {//比较值根据下表去相互替换
int temp = arr[i];//这是需要变更的下标值 arr[i] = arr[j]; arr[j] = temp; }3、插入排序(Insertion Sort)
1、动态图:
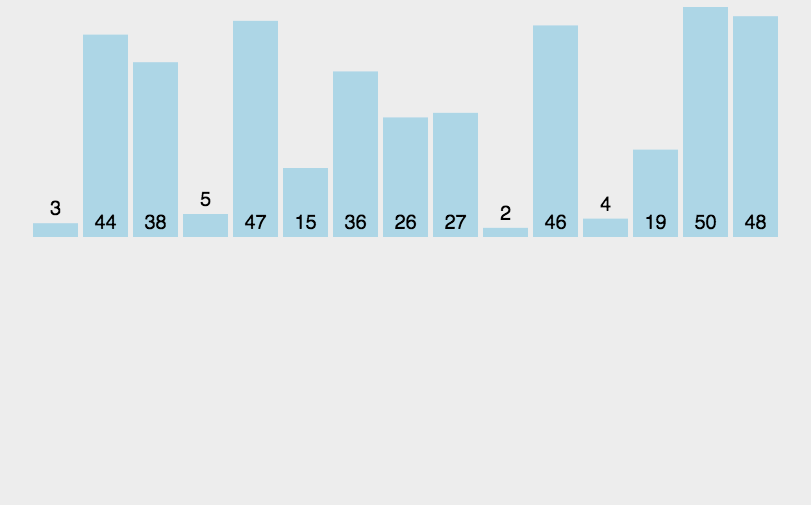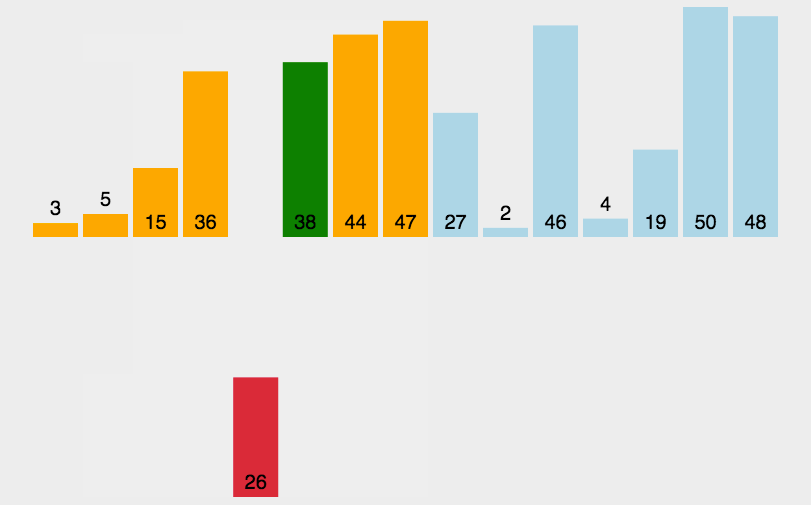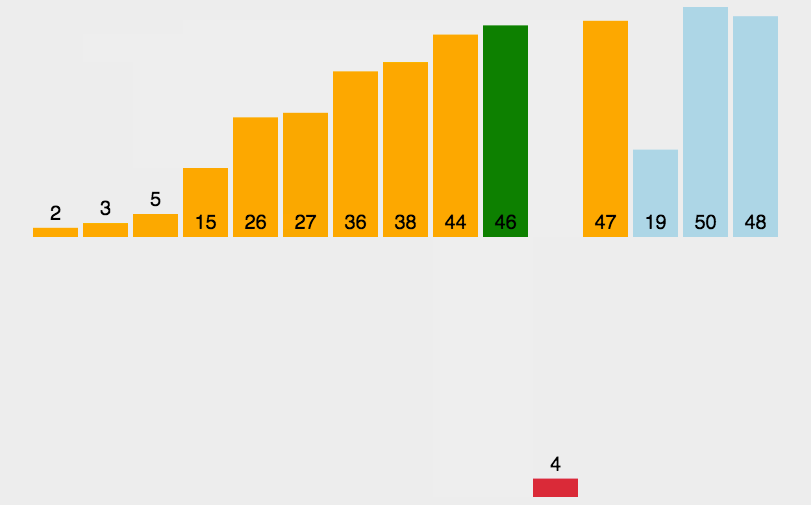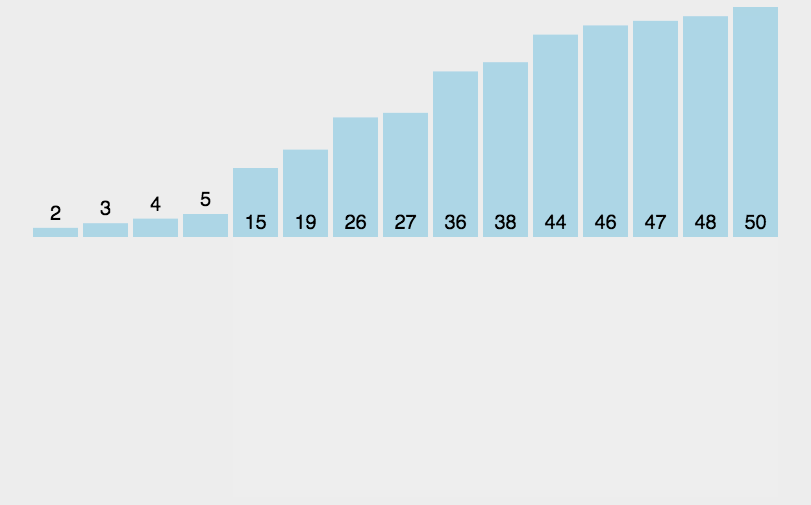
2、算法思想:
在要排序的一组数中,假定前n-1个数已经排好序,现在将第n个数插到前面的有序数列中,使得这n个数也是排好顺序的。如此反复循环,直到全部排好顺序。
3:列子:
Integer[] number = NumberUtil.getNumber(100000,1,100000);
long start=System.currentTimeMillis(); for (int i = 0; i < number.length - 1; i++) { int current = number[i + 1]; int preIndex = i; while (preIndex >= 0 && current < number[preIndex]) { number[preIndex + 1] = number[preIndex]; preIndex--; } number[preIndex + 1] = current;}long end=System.currentTimeMillis();System.out.println("用时:"+(end-start));System.out.println(Arrays.toString(number));4工具方法:
public static Integer[] getNumber(int n,int startNum,int endNum){
Integer [] val=new Integer[n]; for(int i=0;i<n;i++){ val[i]=new Integer((int)(Math.random()*(endNum-startNum))+startNum); } return val; }4、希尔排序(Shell Sort)
1、动态图
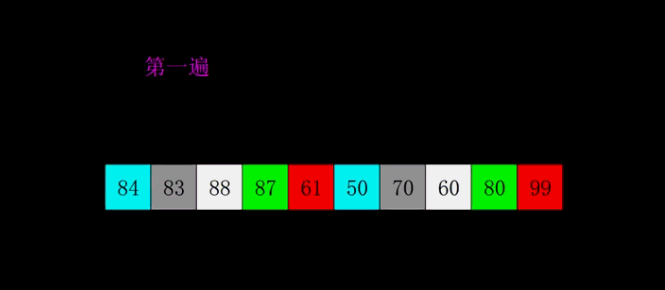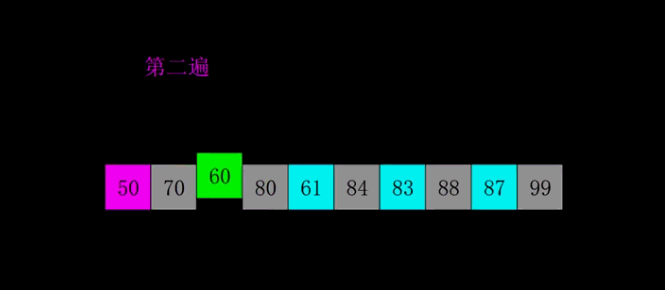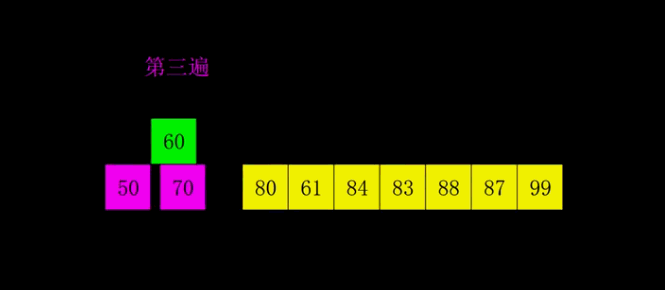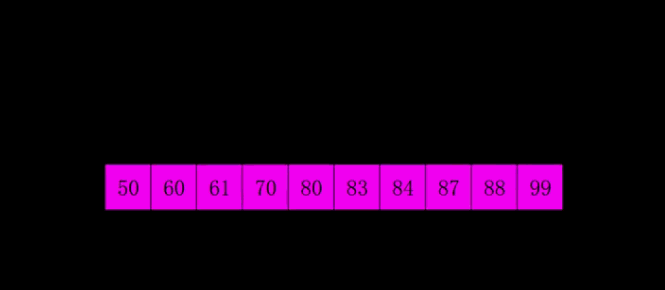
2、算法思想:
希尔排序也是一种插入排序,它是简单插入排序经过改进之后的一个更高效的版本,也称为缩小增量排序,同时该算法是冲破O(n2)的第一批算法之一。它与插入排序的不同之处在于,它会优先比较距离较远的元素。
3、实现列子:
public static void main(String[] args) {
int[] array = { 11, 1, 22, 33, 55, 44, 3 }; int arr1=array.length; int index1,index2=arr1/2; while (index2>0) { for (int i = index2; i < arr1; i++) { index1=array[i]; int preIndex =i-index2; while (preIndex>=0&&array[preIndex]>index1) { array[preIndex + index2] = array[preIndex]; preIndex -= index2; } array[preIndex + index2] = index1; } index2 /= 2; } System.out.println(Arrays.toString(array)); }5、归并排序(Merge Sort)
1、动态图:
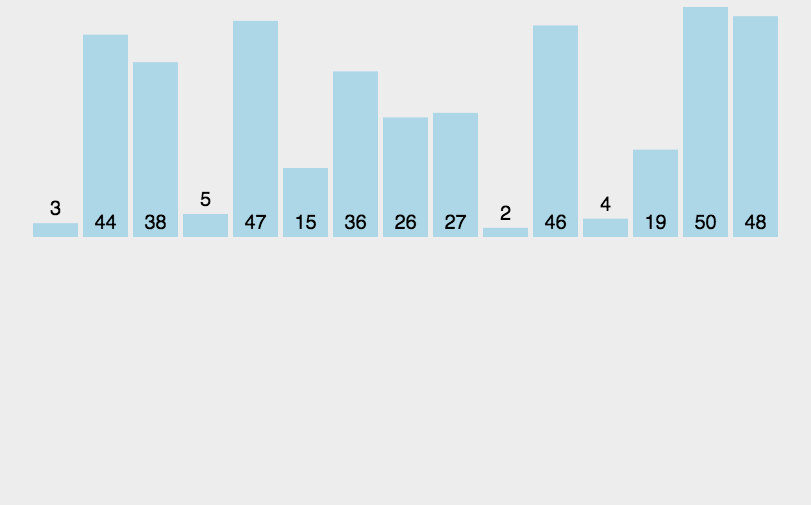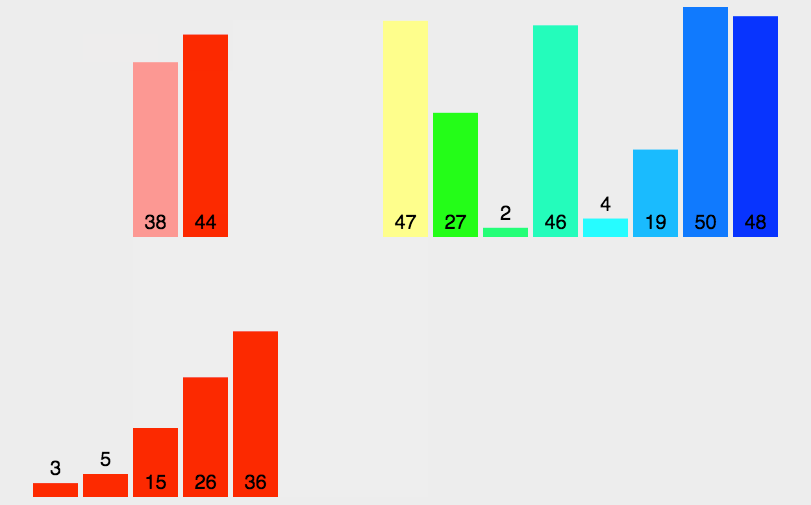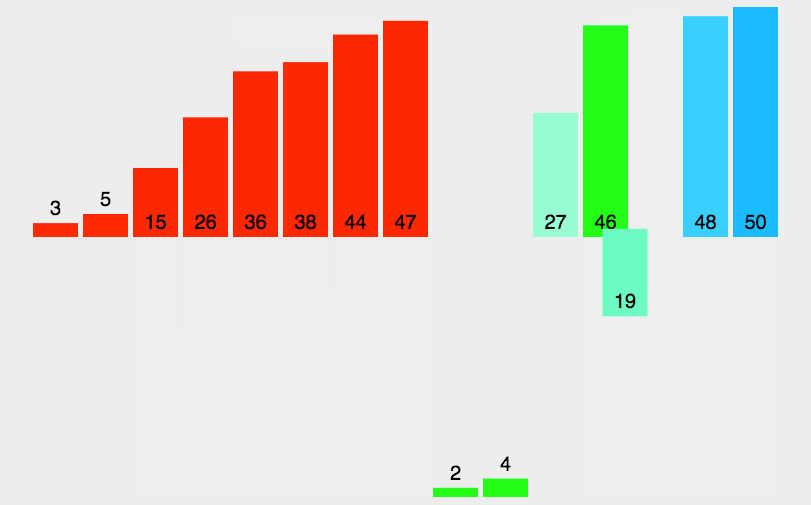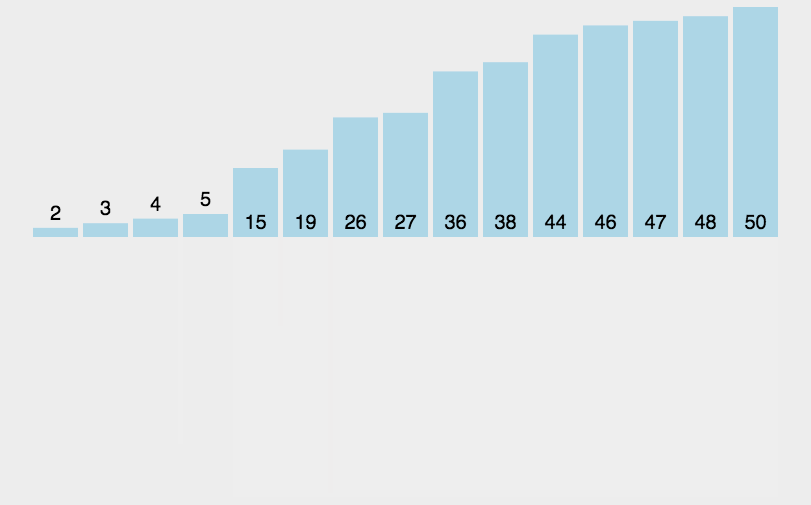
2、基本思想:
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列
3、实现列子:
Arrays.copyOfRange(array, 0, mid);
第一个参数表示源数组第二个参数表示开始位置(取得到)第三个参数表示结束位置(取不到)
public static void main(String[] args) {
int[] array = { 11, 1, 22, 33, 55, 44, 3 }; int[] sort2 = sort(array); System.out.println(Arrays.toString(sort2)); }private static int[] sort(int [] array) {
// TODO Auto-generated method stub if(array.length<2){ return array; } int mid = array.length / 2; int[] left = Arrays.copyOfRange(array, 0, mid); int[] right = Arrays.copyOfRange(array, mid, array.length); return merge(sort(left), sort(right));}
public static int[] merge(int[] left, int[] right) {
int[] result = new int[left.length + right.length]; for (int index = 0, i = 0, j = 0; index < result.length; index++) { if (i >= left.length) result[index] = right[j++]; else if (j >= right.length) result[index] = left[i++]; else if (left[i] > right[j]) result[index] = right[j++]; else result[index] = left[i++]; } return result; }
