本文共 5181 字，大约阅读时间需要 17 分钟。

1. 整型

有符号整型

类型	字节数	最大值	最小值
short	16	2^15 -1 （32767）	-2^15（-32768）
int	32	2^31 -1	-2^31
long	32位系统： long = int , 32； 64位系统： 64	32位系统： 2^31 -1； 64位系统： 2^63 -1	32位系统：- 2^31； 64位系统： -2^63
long long	64	2^63-1	-2^63

无符号整型

类型	字节数	最大值	最小值
short	16	2^16-1	0
int	32	2^32-1	0
long	32位系统： long = int , 32； 64位系统： 64	32位系统： 2^32-1； 64位系统： 2^64-1	0
long long	64	2^64-1	0

示例：

1000000000000001 有符号： -1 无符号： 32769

代码获取字节数， 最大最小值

cout << "short size:" << sizeof(short) << endl;    cout << "int size:" << sizeof(int) << endl;    cout << "long size:" << sizeof(long) << endl;    cout << "long long size:" << sizeof(long long) << endl;    	cout << INT_MAX << endl;    cout << UINT_MAX << endl;    cout << ULONG_LONG_MAX << endl;

溢出

int value1 = INT_MAX + 1;   	// 01111111111111111111111111111111 + 1 = 10000000000000000000000000000000 =  -0,	// 计算器默认赋值为INT_MIN = -2147483648    unsigned int value2 = UINT_MAX + 1;       // 11111111111111111111111111111111 + 1 = 100000000000000000000000000000000 = 0,33位，取32位为0		int value1 = INT_MAX + 2;   	// 10000000000000000000000000000000 + 1 = 10000000000000000000000000000001 =  -1,	// 计算器存储负数使用补码(符号位不变， 0->1, 1->0,再加1)	// 10000000000000000000000000000000  补码: 	// 11111111111111111111111111111111 + 1 = 10000000000000000000000000000000 = INT_MIN = -2147483648	// -2147483648 + 1 = -2147483647    unsigned int value2 = UINT_MAX + 2;       // 100000000000000000000000000000000 + 1 = 100000000000000000000000000000001 = 1,33位，取32位为1

---

2. 字符型

char

cout << "请输入一个字符：";    cin >> c;    // 输出为ASCII码    cout << "已经接收到的字符:" << c << endl; // 输入字符会输出字符，输入整数会输出数字    // 输出为字符,put方法用于向控制台输出字符，即使参数值类型是整数，也会按ASCII输出字符    cout.put(c);

char分为有符号和无符号类型

有符号取值范围为：-2^7 — 2^7-1 　　 [-128, 127] 无符号取值范围为：-0— 2^8-1 　　　 [0, 255]

宽字符

类型	字节数	赋值前缀
wchar_t	32	L
char16_t　 (c++ 11)	16	u
char32_t　 (c++ 11)	32	U

char c = 'a';    wchar_t c1 = L'a';    char16_t c2 = u'a';    char32_t c3 = U'a';        cout << c << endl;  // 输出a    wcout << c1 << endl; // 输出a      char16_t cc = u'中';    cout << cc << endl; // 输出 20013    cout << "\u4E2D" << endl; //转为16进制输出 中    // char16_t 转为 wchar_t    wcout << (wchar_t)c2 << endl; // 输出a

特殊字符

0 - 9 　0:48

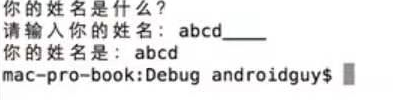
a - z 　a:97 A -Z 　A:65 \n：NewLine \t：tab（水平） \v：tab（垂直） \b：backspace \a：alert 输出警告音 \：输出“\” \’：输出单引号 \"：输出双引号

cout << argv[0] << endl;    cout << (char)7 << "你的姓名是什么？\n";    cout << "请输入你的姓名：________\b\b\b\b\b\b\b\b";    string name;    cin >> name;    cout << "\a你的姓名是：" << name << endl;

运行结果：

---

3. 布尔

ANSI/ISO C++ Standard 加入了bool类型

bool flag1 = true;    bool flag2 = false;    if(flag1 == true && flag2 == false)    {           cout << "条件满足" << endl;    }    //  0：false  非0：true    bool value1 = 100;    bool value2 = 0;    if(value1 && !value2)    {           cout << "value1等于true，value2等于false" << endl;    }

---

4. 浮点型

类型	字节数	取值范围（十进制）	精度
单精度浮点类型：float	4 sizeof(float)	-37 ~ +38	6到7位
双精度浮点类型：double	8 sizeof(double)	-307 ~ 308	15到16位
长双精度浮点类型：long double	16 sizeof(long double)	-4931 ~ 4932	18到19

精度是由尾数位决定的。浮点数在内存中是按照科学计数法来存储的，其整数部分始终是一个隐藏着的1。由于他是不变的，因此对精度不会造成影响

float 尾数为23位， 2^23 = 8,388,608, 7位数，并不是所有七位数都可以表示，所以精度为6到7位

double 尾数为52位， 2^52 = 4,503,599,627,370,496, 16位数

代码获取取值范围和精度

#include 
   
        int f_max = FLT_MAX_10_EXP;    int d_max = DBL_MAX_10_EXP;    int ld_max = LDBL_MAX_10_EXP;        int f_dig = FLT_DIG;  // 6    int d_dig = DBL_DIG;  // 15    int ld_dig = LDBL_DIG; // 18
   

十进制浮点数转换为二进制浮点数

十进制整数转换为二进制整数

// 将十进制整数转为二进制整数    bitset<32> myset(443);    cout << myset << endl;

十进制浮点数转为二进制浮点数

示例：20.5

20 -> 10100

小数位转二进制，每次取小数位2，取整数

0.52 = 1.0 (1)

02 = 0 (0)

02 = 0 (0) …

0.5 -> 1.0

20.5 -> 10100.1

示例： 20.3

20 -> 10100

0.32 = 0.6 (0)

0.62 = 1.2 (1)

0.22 = 0.4 (0)

0.42 = 0.8(0)

0.82=1.6 (1)

0.62 = 1.2 (1)

0.22 = 0.4 (0)

0.42 = 0.8(0)

0.8*2=1.6 (1)

0.3 -> 010011001…1001

20.3 -> 10100.0100110011001…1001

浮点类型的表达方式

采用科学计数法，分为三部分：

1. 尾数
2. E/e
3. 指数

举例 ： 1234500000000000 采用科学计数法 ： 1.2345E15

float f2 = 3e2; //3*10^2     cout << "f2 = " << f2 << endl;      float f3 = 3e-2; //3*0.1^2     cout << "f3 = " << f3 << endl;

浮点型存储方式

类型	符号位	指数位	尾数位
float	1	8	23
double	1	11	52
long double	1	64	63

float的指数范围为-127 ~ 128，double的范围是-1023 ~ 1024， long double的范围为 -2^63-1 ~ 2^63

示例：20.5

二进制： 10100.1

科学计数法： 1.01001E4 = 1.01001E100

存储： 0-10000011-01001000000000000000000

　科学计数法中的E是可以出现负数的，所以IEEE 754规定，E的真实值必须再减去一个中间数（以移位存储），对于8位的E，这个中间数是127；对于11位的E，这个中间数是1023

　2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即10001001

　2^4的E是4，所以保存成32位浮点数时，必须保存成4+127=131，即10000011

示例：20.3

二进制： 10100.0100110011001…1001

科学计数法： 1.01001E4 = 1.01000100110011001…E100

存储： 0-10000000011-01000100110011001…

代码转换（十进制浮点数 -> 存储方式）

float v1 = 20.3;    unsigned int *n = (unsigned int*)(&v1);    for(int i = 31; i >=0;i--)    {           cout << (*n>>i & 1) << (i == 31 || i == 23?"-":"") ;    }    cout << endl;    double v2 = 20.3;    unsigned long long *m = (unsigned long long*)(&v2);    for(int i = 63; i >=0;i--)    {           cout << (*m>>i & 1) << (i == 63 || i == 52?"-":"") ;    }    cout << endl;

浮点型的输出

// float类型赋值    float f_v = 123.4F;        float v1 = 565.292484256;       printf("%0.7f\n", v1);  // 565.2924805    printf("%0.12f\n", 1e7 / 9.0); // 1111111.111111111008    printf("%0.12f\n", 1e7F / 9.0F); // 11111111.125000000000

不同浮点类型，取相同精度获得的结果可能不一致，取精度时需要慎重考虑