本文共 8189 字，大约阅读时间需要 27 分钟。

优化有两大难题

一是：局部最小值

我们的目标是找到全局最小值，如果局部最小值太多，那我们的优化算法就很容易陷入局部最小而不能自拔，这很明显不是观众愿意看到的剧情。

二是：ill-condition病态问题

解释一下ill-condition。ill-condition对应的是well-condition。

那他们分别代表什么？假设我们有个方程组$AX=b$，我们需要求解$X$。如果$A$或者$b$稍微的改变，会使得$X$的解发生很大的改变，那么这个方程组系统就是ill-condition的，反之就是well-condition的。我们具体举个例子吧：
$$\begin{array}{rlrl}& \text{ equations }& \text{ solution }& \\ \left[\begin{array}{cc}1& 2\\ 2& 3.999\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{c}4\\ 7.999\end{array}\right]& \left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{l}2\\ 1\end{array}\right]\\ \left[\begin{array}{cc}1& 2\\ 2& 3.999\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{l}4.001\\ 7.998\end{array}\right]& \left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{c}-3.999\\ 4.000\end{array}\right]\\ \left[\begin{array}{cc}1.001& 2.001\\ 2.001& 3.998\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{c}4\\ 7.999\end{array}\right]& \left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{c}3.994\\ 0.001388\end{array}\right]\end{array}$$

$$\begin{array}{rlrl}& \text{ equations }& \text{ solution }& \\ \left[\begin{array}{ll}1& 2\\ 2& 3\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{l}4\\ 7\end{array}\right]& \left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{l}2\\ 1\end{array}\right]\\ \left[\begin{array}{ll}1& 2\\ 2& 3\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{l}4.001\\ 7.001\end{array}\right]& \left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{l}1.999\\ 1.001\end{array}\right]\\ \left[\begin{array}{cc}1.001& 2.001\\ 2.001& 3.001\end{array}\right]\left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{l}4\\ 7\end{array}\right]& \left[\begin{array}{l}x\\ y\end{array}\right]& =\left[\begin{array}{l}2.003\\ 0.997\end{array}\right]\end{array}$$

咱们先看上边的那个。第一行假设是我们的$AX=b$，第二行我们稍微改变下$b$，得到的$x$和$y$没改变前的差别很大。第三行我们稍微改变下系数矩阵$A$，可以看到结果的变化也很大。换句话来说，这个系统的解对系数矩阵$A$或者$b$太敏感了。又因为一般我们的系数矩阵$A$和$b$是从实验数据里面估计得到的，所以它是存在误差的，如果我们的系统对这个误差是可以容忍的就还好，但系统对这个误差太敏感了，以至于我们的解的误差更大，那这个解就太不靠谱了。所以这个方程组系统就是ill-conditioned病态的，不正常的，不稳定的，有问题的。

下边那个就叫well-condition的系统了。

对于一个ill-condition的系统，我的输入稍微改变下，输出就发生很大的改变，这不好啊，这表明我们的系统不能实用啊。你想想看，例如对于一个回归问题$y=f(x)$，我们是用训练样本$x$去训练模型$f$，使得$y$尽量输出我们期待的值，例如0。那假如我们遇到一个样本$x’$，这个样本和训练样本$x$差别很小，面对他，系统本应该输出和上面的y差不多的值的，例如0.00001，最后却给我输出了一个0.9999，这很明显不对呀。就好像，你很熟悉的一个人脸上长了个青春痘，你就不认识他了，那你大脑就太差劲了，哈哈。所以如果一个系统是ill-conditioned病态的，我们就会对它的结果产生怀疑。那到底要相信它多少呢？我们得找个标准来衡量吧，因为有些系统的病没那么重，它的结果还是可以相信的，不能一刀切吧。终于回来了，上一篇blog提到的condition number就是拿来衡量ill-condition系统的可信度的。condition number衡量的是输入发生微小变化的时候，输出会发生多大的变化。也就是系统对微小变化的敏感度。condition number值小的就是well-conditioned的，大的就是ill-conditioned的。

condition number定义

如果方阵$A$是非奇异的，那么$A$的condition number定义为：
$$\kappa (A)=\Vert A\Vert \Vert A^{-1}\Vert$$
也就是矩阵$A$的norm乘以它的逆的norm。所以具体的值是多少，就要看你选择的norm是什么了。如果方阵$A$是奇异的，那么$A$的condition number就是正无穷大了。实际上，每一个可逆方阵都存在一个condition number。但如果要计算它，我们需要先知道这个方阵的norm（范数）和Machine Epsilon（机器的精度）。

为什么要范数？范数就相当于衡量一个矩阵的大小，我们知道矩阵是没有大小的，上面例子中要衡量一个矩阵$A$或者向量$b$变化的时候，我们的解$X$变化的大小。所以肯定得要有一个东西来度量矩阵和向量的大小。就是范数，表示矩阵大小或者向量长度。

经过比较简单的证明，对于$AX=b$，我们可以得到以下的结论：
$$\begin{array}{r}\frac{\Vert \Delta x\Vert }{\Vert x\Vert }\le \Vert A\Vert \cdot \Vert A^{-1}\Vert \cdot \frac{\Vert \Delta b\Vert }{\Vert b\Vert }\\ \frac{\Vert \Delta x\Vert }{\Vert x\Vert }\le \kappa (A)\cdot \frac{\Vert \Delta b\Vert }{\Vert b\Vert }\\ \frac{\Vert \Delta x\Vert }{\Vert x+\Delta x\Vert }\le \kappa (A)\frac{\Vert \Delta A\Vert }{\Vert A\Vert }\end{array}$$
也就是我们的解$x$的相对变化和$A$或者$b$的相对变化是有像上面那样的关系的，其中$\kappa (A)$的值就相当于倍率，相当于$x$变化的界。

对condition number来个一句话总结：condition number是一个矩阵（或者它所描述的线性系统）的稳定性或者敏感度的度量，如果一个矩阵的condition number在1附近，那么它就是well-conditioned的，如果远大于1，那么它就是ill-conditioned的，如果一个系统是ill-conditioned的，它的输出结果就不要太相信了。

$L_2$范数对于condition number较差情况的缓解

从优化或者数值计算的角度来说，$L_2$范数有助于处理condition number不好的情况下矩阵求逆很困难的问题。因为目标函数如果是二次的，对于线性回归来说，那实际上是有解析解的，求导并令导数等于零即可得到最优解为：
$$\hat{\mathbf{w}}={\left(X^{T}X\right)}^{-1}{X}^T\mathbf{y}$$
然而，如果当我们的样本$X$的数目比每个样本的维度还要小的时候，矩阵$X^{T}X$将会不是满秩的，也就是$X^{T}X$会变得不可逆，所以$w_{\ast }$就没办法直接计算出来了。或者更确切地说，将会有无穷多个解（因为我们方程组的个数小于未知数的个数）。也就是说，我们的数据不足以确定一个解，如果我们从所有可行解里随机选一个的话，很可能并不是真正好的解，总而言之，我们过拟合了。

但如果加上$L_2$规则项，就变成了下面这种情况，就可以直接求逆了：
$$w^{\ast }={\left(X^{T}X+\lambda I\right)}^{-1}{X}^{T}y$$
这里面，专业点的描述是：要得到这个解，我们通常并不直接求矩阵的逆，而是通过解线性方程组的方式（例如高斯消元法）来计算。考虑没有规则项的时候，也就是$\lambda =0$的情况，如果矩阵XTX的condition number很大的话，解线性方程组就会在数值上相当不稳定，而这个规则项的引入则可以改善condition number。

另外，如果使用迭代优化的算法，condition number太大仍然会导致问题：它会拖慢迭代的收敛速度，而正则项从优化的角度来看，实际上是将目标函数变成λ-strongly convex（λ强凸）的了。这里又出现个λ强凸，啥叫λ强凸呢？

当$f$满足：
$$f(\mathrm{y})\ge \mathrm{f}(\mathrm{x})+<\nabla f(\mathrm{x}),\mathrm{y}-\mathrm{x}>+\frac{\lambda }{2}\Vert \mathrm{y}-\mathrm{x}{\Vert }^2$$
时，我们称f为λ-strongl yconvex函数，其中参数$\lambda >0$。当$\lambda =0$时退回到普通convex函数的定义。

在直观的说明强凸之前，我们先看看普通的凸是怎样的。假设我们让f在x的地方做一阶泰勒近似（一阶泰勒展开忘了吗？$f(x)=f(a)+f’(a)(x-a)+o(||x-a||)）$：
$$f(\mathrm{y})\ge \mathrm{f}(\mathrm{x})+<\nabla f(\mathrm{x}),\mathrm{y}-\mathrm{x}>+o(\Vert \mathrm{y}-\mathrm{x}\Vert )$$
直观来讲，convex 性质是指函数曲线位于该点处的切线，也就是线性近似之上，而 strongly convex 则进一步要求位于该处的一个二次函数上方，也就是说要求函数不要太“平坦”而是可以保证有一定的“向上弯曲”的趋势。专业点说，就是convex 可以保证函数在任意一点都处于它的一阶泰勒函数之上，而strongly convex可以保证函数在任意一点都存在一个非常漂亮的二次下界quadratic lower bound。当然这是一个很强的假设，但是同时也是非常重要的假设。可能还不好理解，那我们画个图来形象的理解下

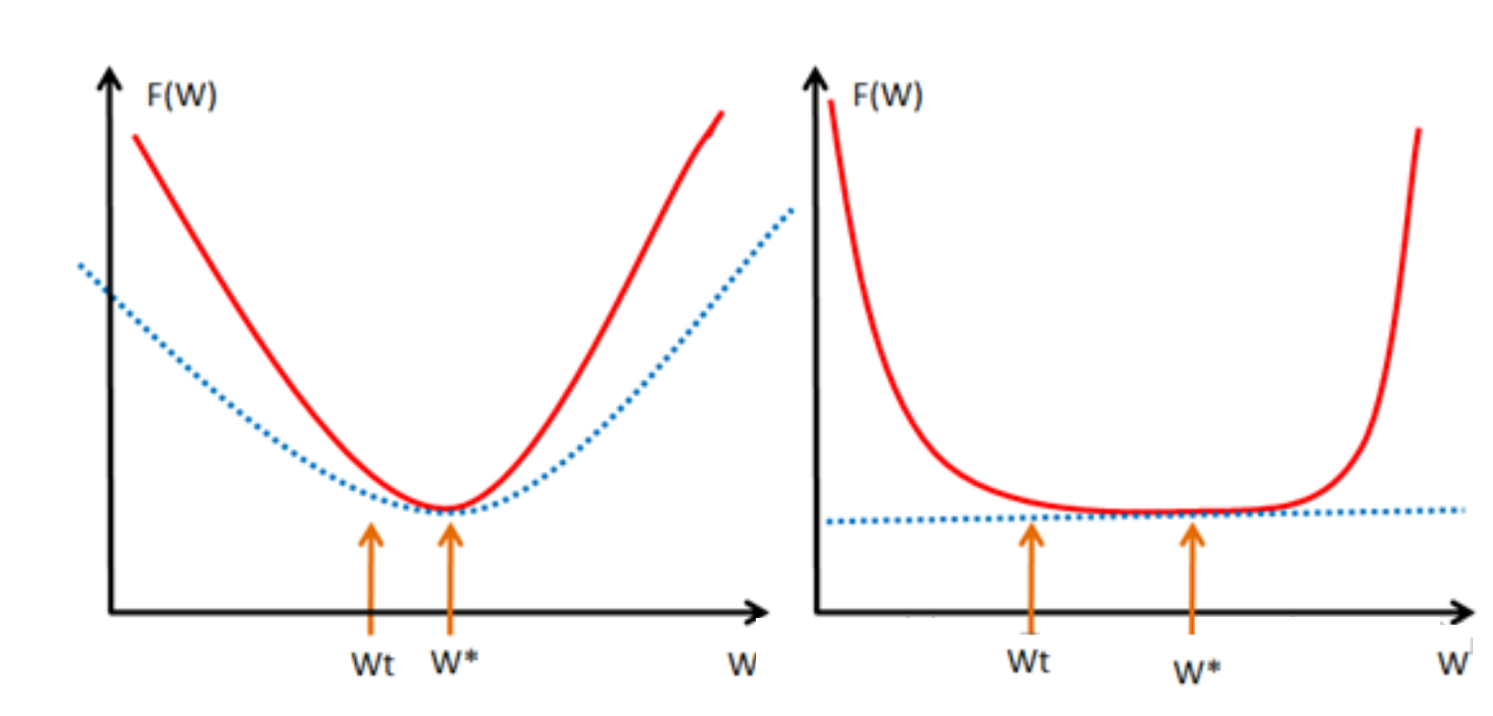
大家一看到上面这个图就全明白了吧。不用我啰嗦了吧。还是啰嗦一下吧。我们取我们的最优解$w_{\ast }$的地方。如果我们的函数$f(w)$，见左图，也就是红色那个函数，都会位于蓝色虚线的那根二次函数之上，这样就算$w_t$和$w_{\ast }$离的比较近的时候，$f(w_t)$和$f(w_{\ast })$的值差别还是挺大的，也就是会保证在我们的最优解$w_{\ast }$附近的时候，还存在较大的梯度值，这样我们才可以在比较少的迭代次数内达到$w_{\ast }$ 。但对于右图，红色的函数$f(w)$ 只约束在一个线性的蓝色虚线之上，假设是如右图的很不幸的情况（非常平坦），那在$w_t$还离我们的最优点$w_{\ast }$很远的时候，我们的近似梯度$\frac{f(w_t)-f(w_{\ast })}{w_t-w_{\ast }}$就已经非常小了，在$w_t$处的近似梯度$\frac{\partial f}{\partial u}$就更小了，这样通过梯度下降$w_t+1=w_t-\alpha \ast \frac{\partial f}{\partial u}$，我们得到的结果就是$w$的变化非常缓慢，像蜗牛一样，非常缓慢的向我们的最优点$w_{\ast }$爬动，那在有限的迭代时间内，它离我们的最优点还是很远。

所以仅仅靠convex 性质并不能保证在梯度下降和有限的迭代次数的情况下得到的点$w$会是一个比较好的全局最小点$w_{\ast }$的近似点（插个话，有地方说，实际上让迭代在接近最优的地方停止，也是一种规则化或者提高泛化性能的方法）。正如上面分析的那样，如果$f(w)$在全局最小点$w_{\ast }$周围是非常平坦的情况的话，我们有可能会找到一个很远的点。但如果我们有“强凸”的话，就能对情况做一些控制，我们就可以得到一个更好的近似解。至于有多好嘛，这里面有一个bound，这个 bound 的好坏也要取决于strongly convex性质中的常数$\alpha$的大小。看到这里，不知道大家学聪明了没有。如果要获得strongly convex怎么做？最简单的就是往里面加入一项$(\alpha /2)\ast ||w||2$。

呃，讲个strongly convex花了那么多的篇幅。实际上，在梯度下降中，目标函数收敛速率的上界实际上是和矩阵$X^{T}X$的 condition number有关，$X^{T}X$的 condition number越小，上界就越小，也就是收敛速度会越快。

$L_2$范数不但可以防止过拟合，还可以让我们的优化求解变得稳定和快速。

LAST、参考文献