本文共 9121 字，大约阅读时间需要 30 分钟。

400

class Solution {
       public int findNthDigit(int n) {
           // num表示具体的整数        int num = 1;        // count表示几位数        int count = 1;        // 9 * num * count 表示几位数总共有多少位数，比如，三位数从100~999，一共是 9 * 100 * 3 = 2700 位数        while (n > 9 * (long) num * count) {
               // 从小到到依次减去一位数、两位数、三位数，直到减不了为止            n -=  9 * num * count;            // num此时记录的是几位数的第一个数，依次是1、10、100、1000            num *= 10;            // count表示几位数，每经过一轮加1，表示下一次判断的位数加1            count++;        }        // 此时的 n 表示从 num 开始取第多少位        // 比如，此时n=5,num=100,count=3，表示从100开始取第5位        // 那么，100是三位，101是三位，所以，第5位肯定在101这个整数的第2位，也就是0        // num += (n - 1) / count; 用来确定是哪个具体的整数了，这里 n-1 是为了防止边界情况，比如n=3,count=3，这时候会取超了        // n -= (n - 1) / count * count; 用来确定是哪个具体的位，n=5-3=2，注意 4/3*3=3，不等于4        // count-n，上面算出来的n是从高到低的第几位，通过 count-n 转成第低到高的第几位        // (num / (int) Math.pow(10, count - n)) % 10; 取出那个位的数字                // 确定是具体哪个整数        num += (n - 1) / count;        // 确定是这个整数中的哪个位        n -= (n - 1) / count * count;        // 取出那个位的数字        return (num / (int) Math.pow(10, count - n)) % 10;    }}作者：tong-zhu链接：https://leetcode.cn/problems/nth-digit/solution/tong-ge-lai-shua-ti-la-zhao-gui-lu-by-to-nvfa/来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

根据

根据这个特性 我们可以逼近n的位数 如果N是个三位数

那么n的位置一定大于9+902

小于9+902+900*3

class Solution {
       public int findNthDigit(int n) {
           // num表示具体的整数        int num = 1;        // count表示几位数        int count = 1;        // 9 * num * count 表示几位数总共有多少位数，比如，三位数从100~999，一共是 9 * 100 * 3 = 2700 位数        while (n > 9 * (long) num * count) {
               // 从小到到依次减去一位数、两位数、三位数，直到减不了为止            n -=  9 * num * count;            // num此时记录的是几位数的第一个数，依次是1、10、100、1000            num *= 10;            // count表示几位数，每经过一轮加1，表示下一次判断的位数加1            count++;        }        // 此时的 n 表示从 num 开始取第多少位        // 比如，此时n=5,num=100,count=3，表示从100开始取第5位        // 那么，100是三位，101是三位，所以，第5位肯定在101这个整数的第2位，也就是0        // num += (n - 1) / count; 用来确定是哪个具体的整数了，这里 n-1 是为了防止边界情况，比如n=3,count=3，这时候会取超了        // n -= (n - 1) / count * count; 用来确定是哪个具体的位，n=5-3=2，注意 4/3*3=3，不等于4        // count-n，上面算出来的n是从高到低的第几位，通过 count-n 转成第低到高的第几位        // (num / (int) Math.pow(10, count - n)) % 10; 取出那个位的数字                // 确定是具体哪个整数        num += (n - 1) / count;        // 确定是这个整数中的哪个位        n -= (n - 1) / count * count;        // 取出那个位的数字        return (num / (int) Math.pow(10, count - n)) % 10;    }}

思路上说的就是是，

将1位数所有数位 + 两位数所有数位 +三位数所有数位减去 不断测试n应该是几位数。 数字长度和位置上个数对应的公式是 len * 9 * pow(10,len - 1)

找到对应的是几位数之后

我们根据几位数的起点 + 偏移量来定位具体是哪个数字 起点是 10 * pow(10,len - 1) 偏移量可以用剩下的n - 1 / (len)

当n价将前几位数的位数都减去之后，剩下的位数 / len就可以得到相对起点的偏移量

注意要用N - 1 因为当n = 15时候 以四位数为例子 1000 1001 1002 1003 1004 1005 1006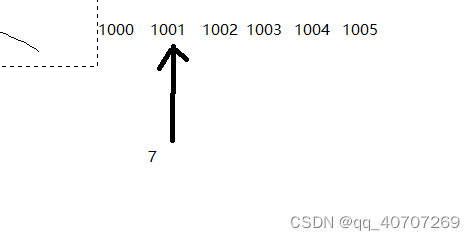 偏移量是 7 / len 得到商是1,也就是可以定位到1000起始点往后偏移1个 定位数字的话也很简单，7对4取余数，可以得到是第几个点

但是注意

如果n取得是4的倍数，那么n / len就是得到一个数

比如n = 8 偏移位就会变成两位，但是实际上是第二个数的最后一位。 所以N - 1是最好的办法，防止越界偏移。 取余数这里也要注意 当N是4的倍数时候，一定要注意，我们取到的是数字的最后一位。

ps:当len大于等于2时候，是从10或者100开始偏移的

当len小于2时候，是从1开始偏移的，这里可以分类讨论。

class Solution {
       public int findNthDigit(int n) {
           if(n < 10){
               return n;        }        // num表示具体的整数        int num = 1;        // count表示几位数        int count = 1;        // 9 * num * count 表示几位数总共有多少位数，比如，三位数从100~999，一共是 9 * 100 * 3 = 2700 位数        while (n > 9 * (long) num * count) {
               // 从小到到依次减去一位数、两位数、三位数，直到减不了为止            n -=  9 * num * count;            // num此时记录的是几位数的第一个数，依次是1、10、100、1000            num *= 10;            // count表示几位数，每经过一轮加1，表示下一次判断的位数加1            count++;        }        // 此时的 n 表示从 num 开始取第多少位        // 比如，此时n=5,num=100,count=3，表示从100开始取第5位        // 那么，100是三位，101是三位，所以，第5位肯定在101这个整数的第2位，也就是0        // num += (n - 1) / count; 用来确定是哪个具体的整数了，这里 n-1 是为了防止边界情况，比如n=3,count=3，这时候会取超了        // n -= (n - 1) / count * count; 用来确定是哪个具体的位，n=5-3=2，注意 4/3*3=3，不等于4        // count-n，上面算出来的n是从高到低的第几位，通过 count-n 转成第低到高的第几位        // (num / (int) Math.pow(10, count - n)) % 10; 取出那个位的数字                // 确定这个数位的第几个数        int pos = (n - 1) / count;        // 确定是哪个整数        //当前数位最小值 + num        int pos2 = n % count == 0 ? count : n % count;//知道是第几位        n =  (int)Math.pow(10,count - 1) + pos;//确认是谁        //                       // 取出那个位的数字        int result =  (n / (int) Math.pow(10, count - pos2)) % 10;        return result;    }}

42接雨水

一层一层计算，先从第I层开始

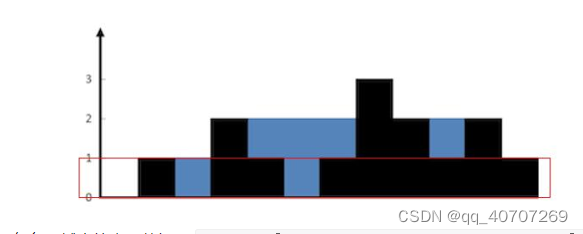
当计算第I层时候，用一个temp

和一个标志位flag 当遇到第一个height[]不为0的时候，说明标志位开始了，可以开始统计了，左边柱子有了，当heigh[]不为0，说明可以temp++啦，这里有水了，遇到height[] < i说明++存进来一格子水

遇到height[] >= i并且标志位为true，就可以将水放进总量ans里面了。如此循环，统计每一层，

如果flag始终为flase那么跳出循环返回结果

class Solution {
       public int trap(int[] height) {
           //需要一个flag位置为false        boolean flag = false;        int temp = 0;        int i = 1;//遍历每一层        int ans = 0;//用来返回结果        for(;;i++){
               //最外层是层层增加层数            //里面一层遍历数字,            for(int value : height){
                   //当当前值，小于当前层时候，就是没有墙                if(flag == false && value < i){
                       continue;//直接跳过去                }                //否则flag == true，除了上面那种情况不然必然是true                flag = true;//否则flag开始计算,说明开始计算了                //如果值大于等于i就是一堵墙                //一堵墙就要将前面temp的值放进ans里，temp重新算计                if(value >= i){
                       ans += temp;                    temp = 0;                                                        }                else{
                       //否则就是一个数                    temp++;                }            }            //整个数组这一层遍历好，如果flag没变，说明数组没了            if(!flag){
                   break;//跳出循环就得了            }            //不然重新放置回到false位置            flag = false;//            //temp也要清零，有可能有上面遗留的问题            temp = 0;        }        return ans;    }}

public int trap(int[] height) {
       int sum = 0;    int max = getMax(height);//找到最大的高度，以便遍历。    for (int i = 1; i <= max; i++) {
           boolean isStart = false; //标记是否开始更新 temp        int temp_sum = 0;        for (int j = 0; j < height.length; j++) {
               if (isStart && height[j] < i) {
                   temp_sum++;            }            if (height[j] >= i) {
                   sum = sum + temp_sum;                temp_sum = 0;                isStart = true;            }        }    }    return sum;}private int getMax(int[] height) {
   		int max = 0;		for (int i = 0; i < height.length; i++) {
   			if (height[i] > max) {
   				max = height[i];			}		}		return max;}作者：windliang链接：https://leetcode.cn/problems/trapping-rain-water/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-w-8/来源：力扣（LeetCode）著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

678有效括号字符串

解题思路

栈(先进后出) 定义两个栈，leftStack 存 ’ ( ’ 所在位置的下标，starStack 存 ‘*’ 所在位置的下标。

1.当遇到 ’ ( ’ 时，’ ( ’ 所在位置的下标入栈；当遇到 ’ * ’ 时，’ * ’ 所在位置的下标入栈。

2.当遇到 ’ ) ’ 时，要令 leftStack 中的栈顶元素出栈，若此时 leftStack 为空，则继续看 starStack 是否为空，若不为空则 starStack 栈顶元素出栈，若为空返回则 false (遇到了 ’ ) '，但在这之前一个 ’ ( ’ 和 ’ * ’ 都没遇到，则一定不会匹配)。

3.当字符串全部遍历完时，若 starStack 的长度比 leftStack 的长度要小，则返回 false (有剩余的 ’ ( '，但 ’ * ’ 的数量不够了，则一定不会匹配)；否则，比较两个栈的栈顶元素值的大小，要保证 ’ ( ’ 在 ’ * ’ 的左边(starStack.peek() > leftStack.peek())才能匹配成功，当遇到满足条件的栈顶元素时，栈顶元素出栈，继续比较下一个。只要有一次该条件不满足，则直接返回 false；否则，返回 true。

作者：Booooo_

链接：https://leetcode.cn/problems/valid-parenthesis-string/solution/you-xiao-de-gua-hao-zi-fu-chuan-zhan-lia-w0n2/ 来源：力扣（LeetCode） 著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

这个细节处理，非常好而且非常正确

对于*号来说。关键问题是，它可以随意变成任何东西，任何东西都是对的，

class Solution {
       public boolean checkValidString(String s) {
           int len = s.length();        Stack
   
     leftStack = new Stack<>();        Stack
    
      starStack = new Stack<>();        for (int i = 0; i < len; i++) {
               // 当遇到 ' ( ' 时，' ( ' 所在位置的下标入栈            if (s.charAt(i) == '(') {
                   leftStack.push(i);            // 当遇到 ' * ' 时，' * ' 所在位置的下标入栈            } else if (s.charAt(i) == '*') {
                   starStack.push(i);            // 当遇到 ' ) ' 时            } else {
                   // 如果leftstack不为空，先消耗'('                if (!leftStack.isEmpty()) {
                       leftStack.pop();                // 如果左括号消耗完了                // '*'当左括号来用                // 检查starStack是不是空                } else if (!starStack.isEmpty()) {
                       starStack.pop();                // '*'也消耗完了，现在又遇到')'，故返回false                } else {
                       return false;                }             }           }        // 当字符串全部遍历完时        // 若 starStack 的长度比 leftStack 的长度要小        // 有剩余的 ' ( '，但 ' * ' 的数量不够了，则一定不会匹配        if (starStack.size() < leftStack.size()) {
               return false;        // 如果剩余的 * 的数量大于等于 左括号的数量        // * 号要么当右括号来用， 要么为空         } else {
               while (!starStack.isEmpty() && !leftStack.isEmpty()) {
                   // 为了消耗剩下的左括号，* 的index 必须要比左括号大，才能在左括号的右边                if (leftStack.peek() > starStack.peek()) {
                       return false;                }                // 消耗一对左括号和*                leftStack.pop();                starStack.pop();            }        }        return true;    }}
    
   

必须要存下标，因为，最后只剩下*时候，*号的下标要比括号大。有可能剩下的，括号里，下标有比左括号在前头的。

左括号就没有这个问题，因为，、每一个右括号都优先消耗左括号，遇到一个右括号，就会消耗一个数值最大的左括号，这套体系保证了，不会有数值比较大的左括号存在，因为一定会被消耗，但是星号不一定，因为我们并不优先消耗星号。

转载地址：https://blog.csdn.net/qq_40707269/article/details/124934145 如侵犯您的版权，请留言回复原文章的地址，我们会给您删除此文章，给您带来不便请您谅解！