本文共 2120 字，大约阅读时间需要 7 分钟。

Problem Description
In mathematics, the function d(n) denotes the number of divisors of positive integer n.

For example, d(12)=6 because 1,2,3,4,6,12 are all 12’s divisors.

In this problem, given l,r and k, your task is to calculate the following thing :

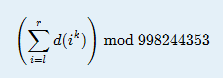
Input
The first line of the input contains an integer T(1≤T≤15), denoting the number of test cases.

In each test case, there are 3 integers l,r,k(1≤l≤r≤1012,r−l≤106,1≤k≤107).

Output
For each test case, print a single line containing an integer, denoting the answer.

Sample Input
3
1 5 1
1 10 2
1 100 3

Sample Output
10
48
2302

Source
2017 Multi-University Training Contest - Team 4
思路：方法都是很容易想到的，肯定是约数定理，k次方的话无非就是再乘k嘛，问题就是如何l和r很大，如何解决超时的问题？由于r-l不超过1e6，所以我么将【l，r】进行平移到【0，r-l】，然后打表1e6的素数，对于那些超过1e6的素数我们最后只要判断一下a【i】是否大于1就知道它本身是不是个素数了。有个细节注意一下，我们枚举素数的时候要从【l，r】中第一个是prime【i】的倍数开始算。

#include<bits/stdc++.h>using namespace std;#define ll long longconst int maxn=1e6+5;const int mod=998244353;int n,d,prime[maxn],top=0,pos[maxn],isprime[maxn]={   0};ll num[maxn],a[maxn];void Prime(int n){       for(int i=2;i<=n;++i)    {           if(!isprime[i]) prime[++top]=i,pos[i]=pos[i-1]+1;        else pos[i]=pos[i-1];         for(int j=1;j<=top;++j)        {               if(i*prime[j]>n) break;            isprime[i*prime[j]]=1;            if(i%prime[j]==0) break;        }    }}int main(){       int T;    Prime(maxn);    scanf("%d",&T);    while(T--)    {           ll ans=0,l,r,k;        scanf("%lld %lld %lld",&l,&r,&k);        for(int i=0;i<=r-l;++i) num[i]=1,a[i]=i+l;        for(int i=1;i<=top;++i)        {               ll s=(l/prime[i])*prime[i];            if(s<l) s+=prime[i];//【l，r】中第一个是prime【i】的倍数            for(ll j=s;j<=r;j+=prime[i])            {                   ll cnt=0;                while(a[j-l]%prime[i]==0)                {                       a[j-l]/=prime[i];                    cnt++;                }                num[j-l]=(num[j-l])*(cnt*k+1)%mod;            }        }        for(int i=0;i<=r-l;++i)        {               if(a[i]>1) num[i]=(num[i]*(k+1))%mod;            ans=(ans+num[i])%mod;         }          printf("%lld\n",ans);    }}