本文共 987 字，大约阅读时间需要 3 分钟。

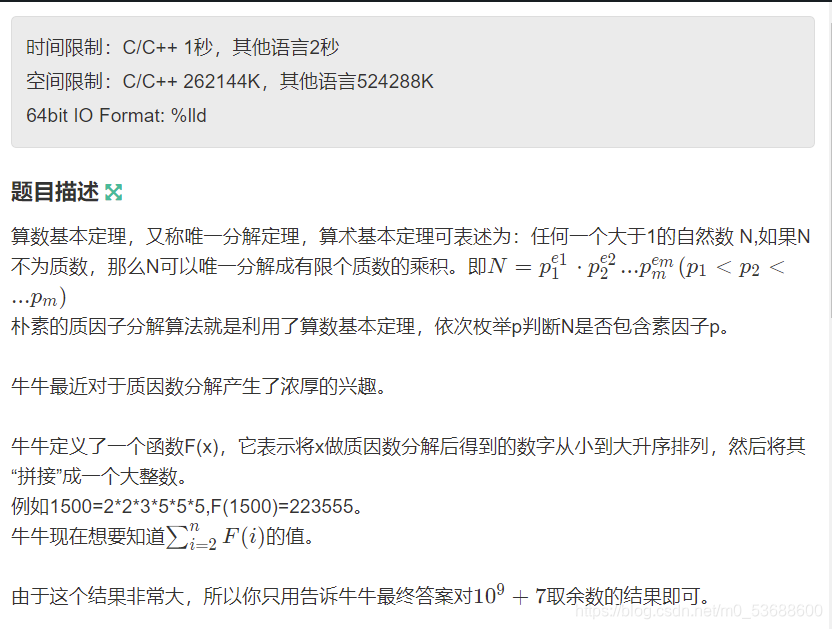
输出描述：

输入：

样例2

输出：

样例2

思路： 核心：素数筛+dp

// 素筛dp#include
   
    using namespace std;typedef long long ll;const int p=1e9+7;ll f[10000000];//每个数的处理后的大整数ll cal(int x) //计算10的x次方{       int ans=10;    while(x--)    {           ans*=10;    }    return ans;}int main(){       ios::sync_with_stdio(false);    cin.tie(0);cout.tie(0);    int n;    cin>>n;    //埃氏筛    for(int i=2; i<=n; i++)    {           if( !f[i] )//如果是素数        {               f[i]=i; //最大素数就是本身            //dp，用对数求要对f[j/i]乘多少个10，因为末尾素数可能很大，前面的数字要前移的位数等于末尾素数的位数            for(int j=i+i ;j<=n ;j+=i)   f[j]=( f[j/i] * cal(log10(i))%p + i)%p;        }    }    ll ans=0;    for(int i=2 ; i<=n ;i++) //最后求和    {           ans= ( ans+f[i] ) %p;    }    cout<
    
     <