本文共 2362 字，大约阅读时间需要 7 分钟。

1. 字典树

1.1 前缀树

前缀树又叫trie树，来自于retrieval，通常用于实现字典查询。本质上，Trie是一颗存储多个字符串的树，最多26叉。每个节点还需要存储引用计数，如果父节点和子节点的计数差1，说明存在到父节点为止的单词。相邻节点间的边代表一个字符，这样树的每条分支代表一则子串，而树的叶节点则代表完整的字符串。我们做即时响应用户输入的AJAX搜索框时，就是Trie树。

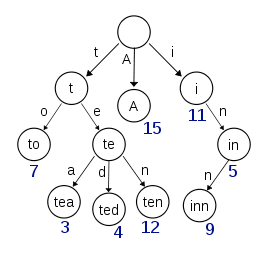
1.2 后缀树

后缀树，就是把一串字符的所有后缀保存并且压缩的字典树。相对于字典树来说，后缀树并不是针对大量字符串的，而是针对一个或几个字符串来解决问题，比如字符串的回文子串，两个字符串的最长公共子串等等。后缀树很容易让人联想到动态规划算法。下面看个例子：

比如单词banana，它的所有后缀显示到下面的。1代表从第一个字符为起点，终点不用说都是字符串的末尾。 以上面的后缀，我们建立一颗后缀树： 下面说下更加节省空间的方案，也就是上面提到的压缩，我们可以将没有分叉的子树用一个数字进行表示：

2. 排序树

索引是对数据库表中一个或多个列的值进行排序的结构。与在表中搜索所有的行相比，索引用指针指向存储在表中指定列的数据值，然后根据指定的次序排列这些指针，有助于更快地获取信息。通常情况下，只有当经常查询索引列中的数据时，才需要在表上创建索引。目前大部分数据库系统及文件系统都采用B-Tree或其变种B+Tree作为索引结构，数据库的IO次数为O(h)=O(logM(n))称为渐进复杂度，传输量为O(M)。

2.1 二叉搜索树(BST)

左树≤根节点≤右树。可以实现二叉搜索的数据结构，理想情况下查找的复杂度从O(n)变为O(log2(n))。

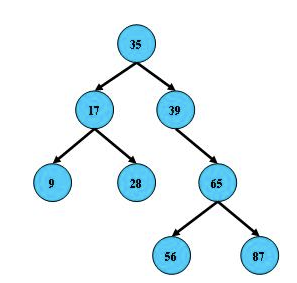但是多次插入与删除后，BST有可能会逐步退化：

2.2 平衡二叉搜索树(AVL)

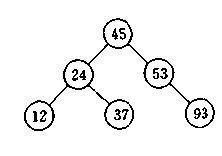
为了防止二叉搜索树退化，AVL要求所有节点的左右子树高度差不超过1。下图是上面的例子与AVL的对比图。

2.3 红黑树(RBT)

对于黑节点是平衡的，并且根节点为黑节点，红节点的子节点必须为黑。红黑是弱平衡的，用非严格的平衡来换取增删节点时候旋转次数的降低；所以简单说，搜索的次数远远大于插入和删除，那么选择AVL树，如果搜索，插入删除次数几乎差不多，应该选择RB树。

2.4 M阶B${}^{-}$树

可以看做是一个多叉排序树。除了根节点外，每个节点有$\lceil m/2\rceil$~$m$个分支，每个节点包含多个值用于分段。查找的复杂度变为O((M-1)logM(n))

2.5 M阶B${}^{+}$树

同样是一个多叉排序树，叶子节点中包含了所有的分叉点，这样全表扫描只需要简单的遍历叶子节点即可。

2.6 M阶B${}^{\ast }$树

在B+树的基础上(所有的叶子结点中包含了全部关键字的信息，及指向含有这些关键字记录的指针)，B树中非根和非叶子结点再增加指向兄弟的指针；B树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3（代替B+树的1/2）。给出了一个简单实例，如下图所示：

B${}^{+}$树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针。 B${}^{\ast }$树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针。 所以，B${}^{\ast }$树分配新结点的概率比B${}^{+}$树要低，空间使用率更高.

2.7 四叉树

将二叉树拓展到二维空间可以得到四叉树。四叉树索引的基本思想是将地理空间递归划分为不同层次的树结构。它将已知范围的空间等分成四个相等的子空间，如此递归下去，直至树的层次达到一定深度或者满足某种要求后停止分割。四叉树的结构比较简单，并且当空间数据对象分布比较均匀时，具有比较高的空间数据插入和查询效率，因此四叉树是GIS中常用的空间索引之一。

2.8 M阶R树

R树全称矩形树（Rectangle Tree），通过外接矩形的包含关系定义排序，是B树在多维下的拓展。和B树一样，所有叶子结点包含有m至M个记录索引（条目）。作为根结点的叶子结点所具有的记录个数可以少于m。通常，m=M/2。所有叶子结点都位于同一层，因此R树为平衡树。下图是一个例子，R8是待查找区域的最小外接矩形：

2.8 排序树应用

B系列的树索引是 MySQL 数据库中使用最为频繁的索引类型，除了 Archive 存储引擎之外的其他所有的存储引擎都支持 B-Tree 索引。Archive 引擎直到 MySQL 5.1 才支持索引，而且只支持索引单个 AUTO_INCREMENT 列。

不仅仅在 MySQL 中是如此，实际上在其他的很多数据库管理系统中B-Tree 索引也同样是作为最主要的索引类型，这主要是因为 B-Tree 索引的存储结构在数据库的数据检索中有非常优异的表现。 MyISAM引擎使用B+Tree作为索引结构，叶节点的data域存放的是数据记录的地址。下图是MyISAM主键索引的原理图： MyISAM索引文件和数据文件是分离的，索引文件仅保存数据记录的地址。而在InnoDB中，表数据文件本身就是按B+Tree组织的一个索引结构，这棵树的叶节点data域保存了完整的数据记录。这个索引的key是数据表的主键，因此InnoDB表数据文件本身就是主索引。