本文共 697 字，大约阅读时间需要 2 分钟。

卷积方式

一开始看到这些卷积名称有点懵，查询后发现就是卷积计算的几种形式，之前学的时候没有这么叫而已。

有效卷积（valid convolution）

使用原始图像，不增加padding。

相同卷积（same convolution）

增加padding使原图和特征图尺寸相等。

跨步卷积（strided convolution）

即为卷积计算设置不同的步长。

体积卷积（convolution over volume）

在处理多通道图像的时候需要用到体积卷积，要求卷积核的通道数与图像的通道数相等。可以看成是对应通道的2D卷积，最后将结果对应位相加，生成2D特征图。

转置卷积（deconvulotion）

转置卷积可以看做是卷积过程的逆运算。

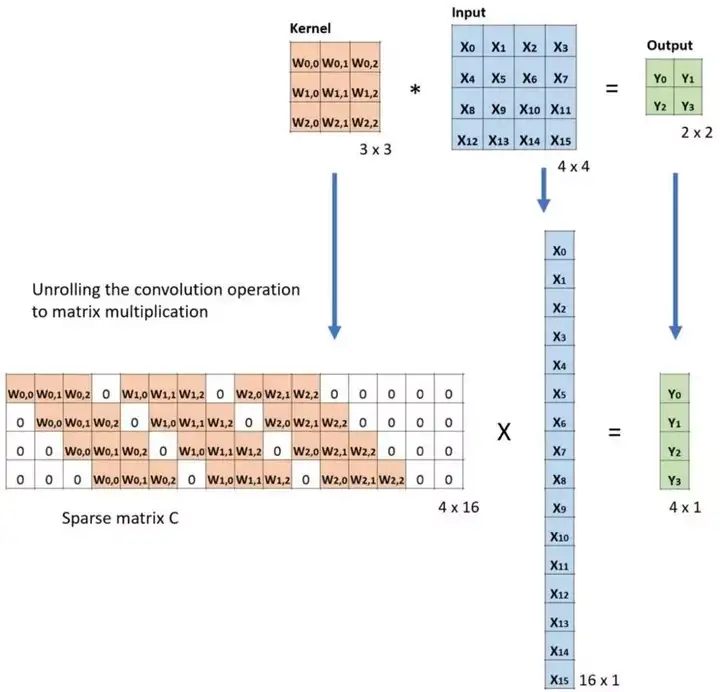
首先，我们可以将卷积的过程展开成矩阵运算：卷积核$\times$输入图像=输出图像。

两边同乘卷积矩阵的转置，得到：转置矩阵$\times$输出图像=输入图像。

从而可以将卷积过程还原，即执行了小图像到大图像的上采样。

卷积核尺寸

为什么常用奇数尺寸的卷积核

在深度学习中，我们用到的卷积核尺寸通常是奇数，如1*1,3*3等。原因有两点：

1. 如果是same convolution，大小为n*n，用k*k的卷积核卷积，步长S为1，满足$n-k+2p+1=n\Rightarrow k=2p+1$。故k为奇数。
2. 卷积核一般使用正方形的，尺寸为奇数才存在中心点。方便以中心点为基准移动，且将结果储存在中心点。如果是偶数则不方便。