本文共 7542 字，大约阅读时间需要 25 分钟。

目录

二分查找

搜索是在一个项目集合中找到一个特定项目的算法过程。搜索通常的答案是真的或假的，因为该项目是否存在。 搜索的几种常见方法：顺序查找、二分法查找、二叉树查找、哈希查找

二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。首先，假设表中元素是按升序排列，将表中间位置记录的关键字与查找关键字比较，如果两者相等，则查找成功；否则利用中间位置记录将表分成前、后两个子表，如果中间位置记录的关键字大于查找关键字，则进一步查找前一子表，否则进一步查找后一子表。重复以上过程，直到找到满足条件的记录，使查找成功，或直到子表不存在为止，此时查找不成功。

# 快排def quick_sort(list, start, end):    if start >= end:        return    low = start    high = end    mid = list[start]    while low < high:        while low < high and list[high] >= mid:            high -= 1        list[low] = list[high]        while low < high and list[low] < mid:            low += 1        list[high] = list[low]    list[low] = mid    quick_sort(list, start, low-1)    quick_sort(list, low+1, end)# 递归二分def recursion_binary_search(list,item):    n = len(list)    if n > 0:        mid = n//2        if list[mid] == item:            return True        elif list[mid] > item:            return recursion_binary_search(list[:mid], item)        elif list[mid] < item:            return recursion_binary_search(list[mid+1:], item)    return False# 非递归二分def binary_search(list,item):    n = len(list)    first = 0    last = n - 1    while first <= last:        mid = (first + last) // 2        if list[mid] == item:            return True        elif list[mid] > item:            last = mid - 1        elif list[mid] < item:            first = mid + 1    return Falseif __name__ == "__main__":    li = [54, 26, 93, 17, 55, 55, 44, 55, 20]    quick_sort(li, 0, len(li)-1)    print(li)    print(recursion_binary_search(li, 51))    li2 = [54, 226, 93, 17, 77, 31, 100, 55, 20]    quick_sort(li2, 0, len(li2) - 1)    print(li2)    print(binary_search(li2, 77))    print(binary_search(li2, 78))# /Users/mintou/Desktop/PYCharm/venv/bin/python /Users/mintou/Desktop/PYCharm/01-test.py# [17, 20, 26, 44, 54, 55, 55, 55, 93]# False# [17, 20, 31, 54, 55, 77, 93, 100, 226]# True# False## Process finished with exit code 0

这里可以和数据库Mysql索引相联系起来，其中索引是通过B-tree外键表来维护

MySQL官方对索引的定义为：索引（Index）是帮助MySQL高效获取数据的数据结构。提取句子主干，就可以得到索引的本质：索引是数据结构。

我们知道，数据库查询是数据库的最主要功能之一。我们都希望查询数据的速度能尽可能的快，因此数据库系统的设计者会从查询算法的角度进行优化。最基本的查询算法当然是（linear search），这种复杂度为O(n)的算法在数据量很大时显然是糟糕的，好在计算机科学的发展提供了很多更优秀的查找算法，例如（binary search）、（binary tree search）等。如果稍微分析一下会发现，每种查找算法都只能应用于特定的数据结构之上，例如二分查找要求被检索数据有序，而二叉树查找只能应用于上，但是数据本身的组织结构不可能完全满足各种数据结构（例如，理论上不可能同时将两列都按顺序进行组织），所以，在数据之外，数据库系统还维护着满足特定查找算法的数据结构，这些数据结构以某种方式引用（指向）数据，这样就可以在这些数据结构上实现高级查找算法。这种数据结构，就是索引。

时间复杂度

• 最优时间复杂度：O(1)
• 最坏时间复杂度：O(logn)

树的种类

• 无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树；
• 有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；
  • 二叉树：每个节点最多含有两个子树的树称为二叉树；
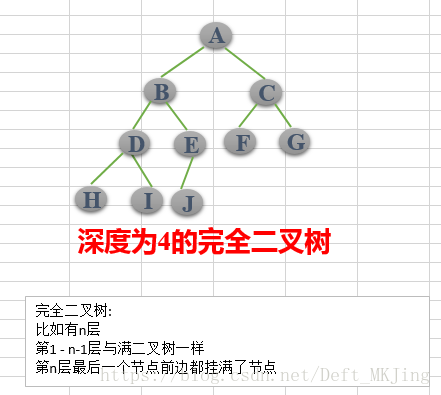
    • 完全二叉树：对于一颗二叉树，假设其深度为d(d>1)。除了第d层外，其它各层的节点数目均已达最大值，且第d层所有节点从左向右连续地紧密排列，这样的二叉树被称为完全二叉树，其中满二叉树的定义是所有叶节点都在最底层的完全二叉树;
    • 平衡二叉树（AVL树）：当且仅当任何节点的两棵子树的高度差不大于1的二叉树；
    • 排序二叉树（二叉查找树（英语：Binary Search Tree），也称二叉搜索树、有序二叉树）；
  • 霍夫曼树（用于信息编码）：带权路径最短的二叉树称为哈夫曼树或最优二叉树；
  • B树：一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多余两个子树。

二叉树的性质(特性)

性质1: 在二叉树的第i层上至多有2^(i-1)个结点（i>0）
性质2: 深度为k的二叉树至多有2^k - 1个结点（k>0）
性质3: 对于任意一棵二叉树，如果其叶结点数为N0，而度数为2的结点总数为N2，则N0=N2+1;
性质4:具有n个结点的完全二叉树的深度必为 log2(n+1)
性质5:对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号必为2i＋1；其双亲的编号必为i/2（i＝1 时为根,除外）

(1)完全二叉树——若设二叉树的高度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第h层有叶子结点，并且叶子结点都是从左到右依次排布，这就是完全二叉树

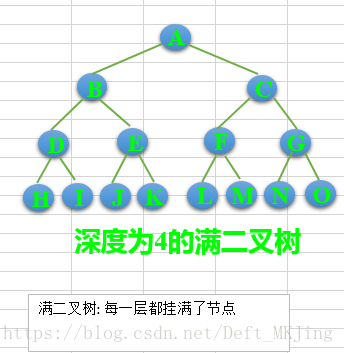
(2)满二叉树——除了叶结点外每一个结点都有左右子叶且叶子结点都处在最底层的二叉树。

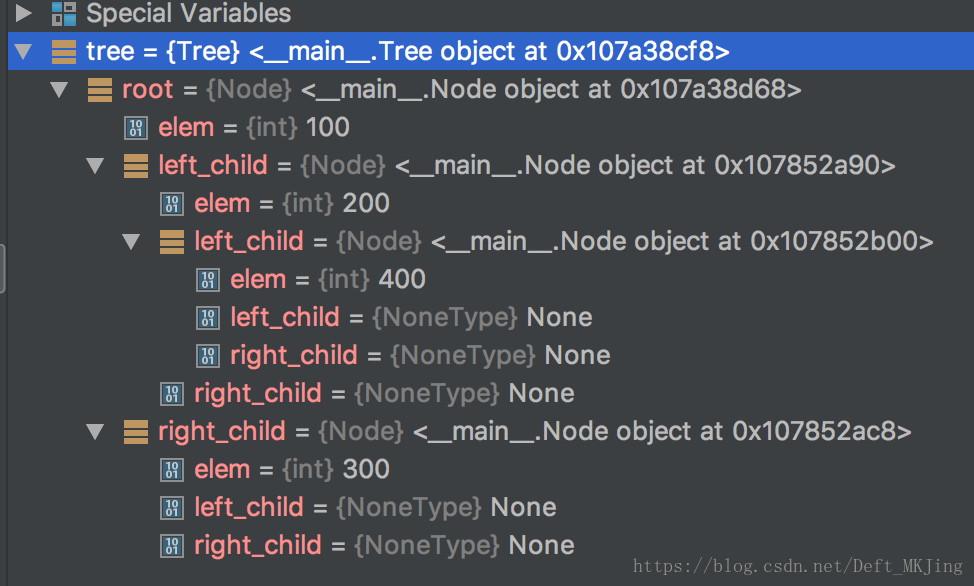
二叉树的节点表示以及树的创建

class Node(object):    """节点类"""    def __init__(self, elem):        self.elem = elem        self.left_child = None        self.right_child = Noneclass Tree(object):    def __init__(self):        self.root = None    def add(self, element_node):        node = Node(element_node)        if self.root is None:            self.root = node            return        queue = [self.root]        while queue:            cur_node = queue.pop(0)            if cur_node.left_child is None:                cur_node.left_child = node                return            elif cur_node.right_child is None:                cur_node.right_child = node                return            else:                queue.append(cur_node.left_child)                queue.append(cur_node.right_child)if __name__ == "__main__":    tree = Tree()    tree.add(100)    tree.add(200)    tree.add(300)    tree.add(400)    print(tree)

二叉树的遍历

树的遍历是树的一种重要的运算。所谓遍历是指对树中所有结点的信息的访问，即依次对树中每个结点访问一次且仅访问一次，我们把这种对所有节点的访问称为遍历（traversal）。那么树的两种重要的遍历模式是深度优先遍历和广度优先遍历,深度优先一般用递归，广度优先一般用队列。一般情况下能用递归实现的算法大部分也能用堆栈来实现。

广度遍历

    # 广度遍历 用队列    def breadth_travel(self):        if self.root is None:            return        queue = [self.root]        while queue:            cur_node = queue.pop(0)            print(cur_node.elem)            if cur_node.left_child is not None:                queue.append(cur_node.left_child)            if cur_node.right_child is not None:                queue.append(cur_node.right_child)

深度遍历（先序 中序 后序）

对于一颗二叉树，深度优先搜索(Depth First Search)是沿着树的深度遍历树的节点，尽可能深的搜索树的分支。
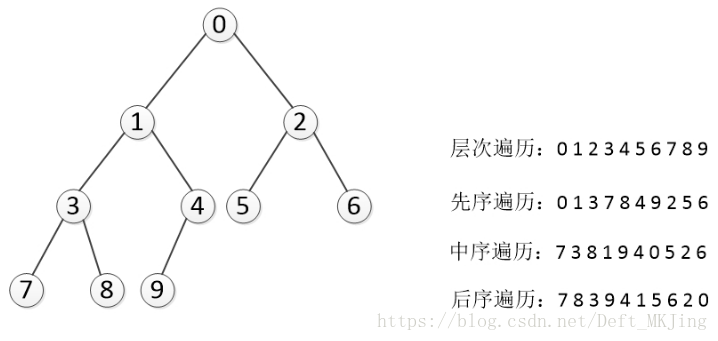
那么深度遍历有重要的三种方法。这三种方式常被用于访问树的节点，它们之间的不同在于访问每个节点的次序不同。这三种遍历分别叫做先序遍历（preorder 根 左 右），中序遍历（inorder 左 根 右）和后序遍历（postorder 左 右 根）。我们来给出它们的详细定义，然后举例看看它们的应用。

class Node(object):    """节点类"""    def __init__(self, elem):        self.elem = elem        self.left_child = None        self.right_child = Noneclass Tree(object):    def __init__(self):        self.root = None    def add(self, element_node):        node = Node(element_node)        if self.root is None:            self.root = node            return        queue = [self.root]        while queue:            cur_node = queue.pop(0)            if cur_node.left_child is None:                cur_node.left_child = node                return            elif cur_node.right_child is None:                cur_node.right_child = node                return            else:                queue.append(cur_node.left_child)                queue.append(cur_node.right_child)    # 广度遍历 用队列    def breadth_travel(self):        if self.root is None:            return        queue = [self.root]        while queue:            cur_node = queue.pop(0)            print(cur_node.elem, end=" ")            if cur_node.left_child is not None:                queue.append(cur_node.left_child)            if cur_node.right_child is not None:                queue.append(cur_node.right_child)    # 前序遍历 根 左 右    def pre_order(self, node):        if node is None:            return        print(node.elem, end=" ")        self.pre_order(node.left_child)        self.pre_order(node.right_child)    # 中序遍历 左 右 根    def mid_order(self, node):        if node is None:            return        self.mid_order(node.left_child)        print(node.elem, end=" ")        self.mid_order(node.right_child)    # 后序遍历    def last_order(self, node):        if node is None:            return        self.last_order(node.left_child)        self.last_order(node.right_child)        print(node.elem, end=" ")if __name__ == "__main__":    tree = Tree()    tree.add(0)    tree.add(1)    tree.add(2)    tree.add(3)    tree.add(4)    tree.add(5)    tree.add(6)    tree.add(7)    tree.add(8)    tree.add(9)    # 广度    print("广度遍历")    tree.breadth_travel()    print()    print("*"*50)    # 前序    print("前序遍历")    tree.pre_order(tree.root)    print()    print("中序遍历")    tree.mid_order(tree.root)    print()    print("后序遍历")    tree.last_order(tree.root)/Users/mintou/Desktop/PYCharm/binary_tree.py广度遍历0 1 2 3 4 5 6 7 8 9 **************************************************前序遍历0 1 3 7 8 4 9 2 5 6 中序遍历7 3 8 1 9 4 0 5 2 6 后序遍历7 8 3 9 4 1 5 6 2 0 Process finished with exit code 0

如何根据遍历顺序确定一棵树？

中序肯定是要有的，先序和后序可以选其一，先序或后序用来算出根节点，对应到中序分割左右子树，直至分割完成

结果：
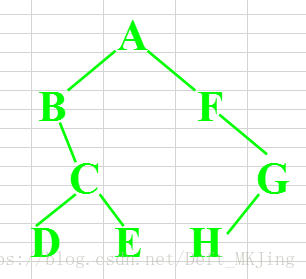
先序:a b c d e f g h
中序:b d c e a f h g
后序:d e c b h g f a

如上图，可以根据先序和中序或者后序和中序得出