
从求解周期矩形脉冲信号的傅里叶级数表达式到初识Gibbs现象
发布日期:2021-05-08 01:17:13
浏览次数:21
分类:精选文章
本文共 380 字,大约阅读时间需要 1 分钟。
[题目要求] 求下图所示周期矩形脉冲信号x(t)的傅里叶级数表达式, 并用Matlab求出由前N项傅里叶级数系数得出的信号近似波形.

[分析]
上述周期矩形脉冲信号的频谱函数Cn = 0.5 * Sa(n * pi / 2), 由连续周期信号的傅里叶级数表达式可知, xN(t) = 0.5 + ∑n = (1, N) Sa(n * pi / 2) * cos(n * pi * t).
[Gibbs现象简介]
一个连续周期信号可以表达为无限项虚指数信号的叠加, 但在实际工程应用中, 我们很难计算无限项虚指数信号的叠加, 我们往往取有限项来近似还原原来的x(t)信号. 当我们取有限项虚指数信号的叠加来表示原来的信号x(t)时, 在原信号的间断点处还是有跳跃, 而且这个跳跃值不随N的变化而变化, 这个值是原来信号幅值变化的9%. 这个现象由Gibbs发现.
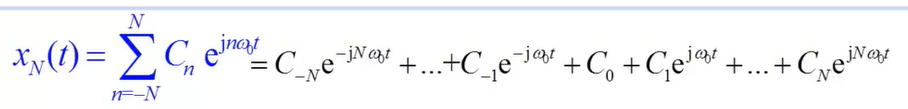
发表评论
最新留言
能坚持,总会有不一样的收获!
[***.219.124.196]2025年04月04日 21时17分55秒
关于作者

喝酒易醉,品茶养心,人生如梦,品茶悟道,何以解忧?唯有杜康!
-- 愿君每日到此一游!
推荐文章
上周热点回顾(1.23-1.29)
2021-05-09
上周热点回顾(3.20-3.26)
2021-05-09
上周热点回顾(6.19-6.25)
2021-05-09
云计算之路-阿里云上:docker swarm 集群故障与异常
2021-05-09
上周热点回顾(2.19-2.25)
2021-05-09
云计算之路-阿里云上:博客web服务器轮番CPU 100%
2021-05-09
云计算之路-阿里云上:服务器CPU 100%问题是memcached连接数限制引起的
2021-05-09
上周热点回顾(3.26-4.1)
2021-05-09
上周热点回顾(6.25-7.1)
2021-05-09
【故障公告】10:30-10:45 左右 docker swarm 集群节点问题引发故障
2021-05-09
工作半年的思考
2021-05-09
不可思议的纯 CSS 滚动进度条效果
2021-05-09
【CSS进阶】伪元素的妙用--单标签之美
2021-05-09
惊闻NBC在奥运后放弃使用Silverlight
2021-05-09
IE下尚未实现错误的原因
2021-05-09
创建自己的Docker基础镜像
2021-05-09
Python 简明教程 --- 20,Python 类中的属性与方法
2021-05-09
KNN 算法-理论篇-如何给电影进行分类
2021-05-09
Spring Cloud第九篇 | 分布式服务跟踪Sleuth
2021-05-09