
本文共 5524 字,大约阅读时间需要 18 分钟。
文章目录
前言
快速排序(Quicksort)是对冒泡排序的一种改进。
介绍
快速排序由C. A. R. Hoare在1960年提出。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
快速排序采用了一种分治的策略,通常称其为分治法(Divide-and-ConquerMethod)。动图演示
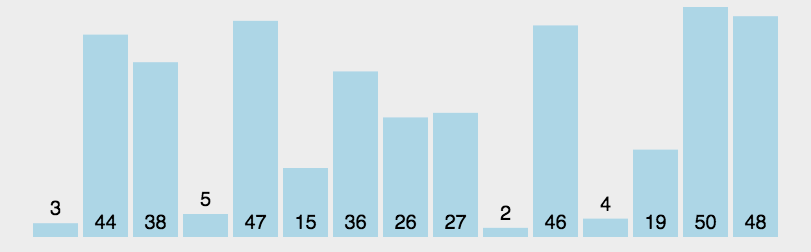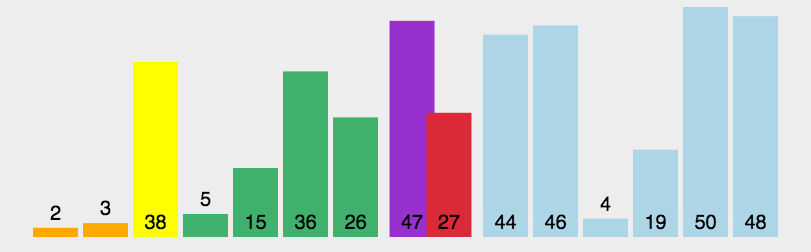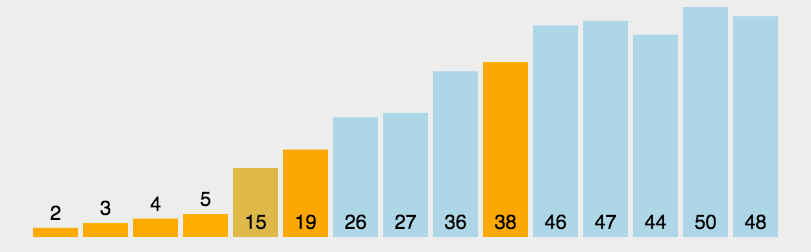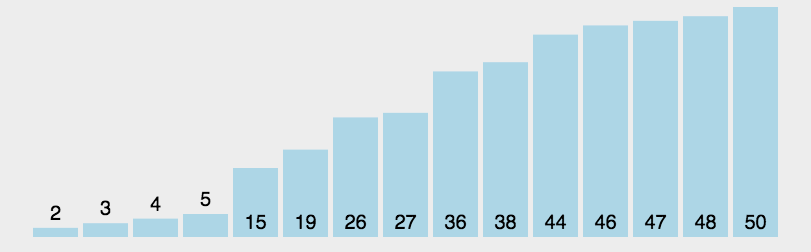
特点

基本思想
- 先从数列中取出一个数作为基准数。
- 分区过程,将比这个数大的数全放到它的右边,小于或等于它的数全放到它的左边。
- 再对左右区间重复第二步,直到各区间只有一个数。
在该篇博客中,将使用挖坑填数法+分治法来对快速排序作出介绍
实现(挖坑法)
假设存在这样一个数组a[10],数组中存在有10个100以下的数:
要使用快速排序给这个数组排序,第一步要做的,就是取基准数。
这里取数组的第一个数(即72)为基准数,为了更直观地体现快速排序的过程,这里用表格形式来显示该组数据:表格①
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 72 | 6 | 57 | 88 | 60 | 42 | 83 | 73 | 48 | 85 |
X=72,i=0,j=9
第一列为数组的索引值,第二列为该数组的每个值,而标红的值(72),即为此次快速排序的基准数
除了取基准值(设为X)之外,我们还要获得该数组开头的索引值(设为i)和结尾的索引值(设为j)。 由该表格可以看出,X=a[0]=72(我们刚刚取出来的),i=0(起始索引),j=9(结尾索引) 由于已经将 a[0] 中的数保存到 X 中,可以理解成在数组 a[0] 上挖了个坑,所以可以将其它数据填充到这来。 接下来,从j开始向前找一个比X小或等于X的数。从表格中可以得知,当j=8时,a[j]=a[8]=48<72,符合条件,于是将a[8]挖出再填到上一个坑a[0]中,即执行a[0] = a[8],并且让i++,这样一个坑a[0]就被填上了,变换后的数组如下所示:表格②
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 48 | 6 | 57 | 88 | 60 | 42 | 83 | 73 | 48 | 85 |
X=72(基准值虽然暂时消失了,但是只要定义了,就不会改变),i=1,j=8
但是不要高兴得太早,因为新坑a[8]出现了。为了处理这个问题,我们使用上次的方法,只不过,这次要从i开始向后找一个大于X的数。从表格中可以得知,当i=3时,a[i]=a[3]=88>72,符合条件,于是将a[3]挖出再填到上一个坑a[8]中,即执行a[8] = a[3],并且让j– ,这样第二个坑a[8]就被填上了,变换后的数组如下所示:
表格③
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 48 | 6 | 57 | 88 | 60 | 42 | 83 | 73 | 88 | 85 |
X=72,i=3,j=7
就跟前面的步骤相似的,这次轮到新坑a[3]出现了,还是参照上面的老方法,从j开始向前找一个比X小或等于X的数。从表格中可以得知,当j=5时,a[j]=a[5]=42<72,符合条件,于是将a[5]挖出再填到上一个坑a[3]中,即执行a[3] = a[5],并且让i++,这样第三个坑a[3]就被填上了,变换后的数组如下所示:
表格④
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 48 | 6 | 57 | 42 | 60 | 42 | 83 | 73 | 88 | 85 |
X=72,i=4,j=5
这次出现的是新坑a[5],按照老规矩,我们从i开始向后找一个大于X的数,但是知道i==j,即两个索引碰头时,也没有找到能大于X的数,那应该怎么填上这个坑呢?
还记得最开始挖的坑a[0] 吗?没错,要填上a[5]这个坑,只能用最开始选取的基准值来填进去,即X,变换后的数组如下:表格⑤
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 48 | 6 | 57 | 42 | 60 | 72 | 83 | 73 | 88 | 85 |
X=72,i=5,j=5
由这个表可以看出:a[5]前面的数字都小于它,a[5]后面的数字都大于它。至此,快速排序的第一轮就结束了。
等等!这个数组好像还没有排序成功吧!
这个时候,就需要用到分治法的思想了。现在整体大致排序好了,我们只需要再对a[0…4]和a[6…9]这二个子区间重复上述步骤就可以了。具体的过程,就不在这里赘述了。
总结
- i =0; j = a.length - 1; 将基准数挖出形成第一个坑(这里建议选择a[0],即数组的第一个值)。
- 由后向前找比它小的数,找到后挖出此数填前一个坑a[i]中,然后记得j–
- 由前向后找比它大的数,找到后也挖出此数填到前一个坑a[j]中,然后记得i++
- 再重复执行2,3二步(切记:顺序不能调换!),直到i==j,最后再将基准数填入a[i]中。
代码实现
/** * @author:Tokgo J * @date:2019/11/27 * @aim:填坑法实现的快速排序,代码使用了递归的方式 */public class QuickSort1 { /** * quickSort方法通过递归的方式,实现了分而治之的思想 * @param arr * @param startIndex * @param endIndex */ public static void quickSort(int[] arr,int startIndex,int endIndex){ //递归结束条件:startIndex大于等于endIndex的时候 if(startIndex>=endIndex){ return; } //得到基准元素位置 int pivotIndex = partition(arr,startIndex,endIndex); //用分治法递归数组的两部分 quickSort(arr,startIndex,pivotIndex-1); quickSort(arr,pivotIndex+1,endIndex); } /** * partition方法则实现元素的移动,让数列中的元素依据自身大小,分别移动到基准元素的左右两边。在这里,我们使用移动方式是挖坑法。 * @param arr * @param startIndx * @param endIndex * @return */ private static int partition(int[] arr,int startIndx,int endIndex){ //取第一个位置的元素作为基准元素 int pivot = arr[startIndx]; int left = startIndx; int right = endIndex; //坑的位置,初始等于pivot的位置 int index = startIndx; //大循环的左右指针重合或者交错时结束 while (right >= left){ //right指针从右向左进行比较 while (right >= left){ if (arr[right] < pivot){ arr[left] = arr[right]; index = right; left++; break; } right--; } //left指针从左向右进行比较 while(right >= left){ if (arr[left] > pivot){ arr[right] = arr[left]; index = left; right--; break; } left++; } } arr[index] = pivot; return index; } public static void main(String[] args) { int[] arr={ 12,23,34,54,12,34,45,56,67,87,54,234,45,65,65,67,87,98}; quickSort(arr,0,arr.length-1); System.out.println(Arrays.toString(arr)); }} 实现(指针交换法)
下面通过一个例子介绍快速排序算法的思想,假设要对数组a[10]={6,1,2,7,9,3,4,5,10,8}进行排序,首先要在数组中选择一个数作为基准值,这个数可以随意选择,在这里,我们选择数组的第一个元素a[0]=6作为基准值,接下来,我们需要把数组中小于6的数放在左边,大于6的数放在右边,怎么实现呢?
我们设置两个“哨兵”,记为“哨兵i”和“哨兵j”,他们分别指向数组的第一个元素和最后一个元素,即i=0,j=9。首先哨兵j开始出动,哨兵j一步一步地向左挪动(即j–),直到找到一个小于6的数停下来。接下来哨兵i再一步一步向右挪动(即i++),直到找到一个数大于6的数停下来。
最后哨兵j停在了数字5面前,哨兵i停在了数字7面前。此时就需要交换i和j指向的元素的值。

 第一次交换至此结束。接下来,由于哨兵i和哨兵j还没有相遇,于是哨兵j继续向前,发现比6小的4之后停下;哨兵i继续向前,发现比6大的9之后停下,两者再进行交换。交换之后的数组变为a[10]={6,1,2,5,4,3,9,7,10,8}。
第一次交换至此结束。接下来,由于哨兵i和哨兵j还没有相遇,于是哨兵j继续向前,发现比6小的4之后停下;哨兵i继续向前,发现比6大的9之后停下,两者再进行交换。交换之后的数组变为a[10]={6,1,2,5,4,3,9,7,10,8}。  第二次交换至此结束。接下来,哨兵j继续向前,发小比6小的3停下来;哨兵i继续向前,发现i==j了!!!于是,这一轮的探测就要结束了,此时交换a[i]与基准的值,数组a就以6为分界线,分成了小于6和大于6的左右两部分:a[10]={3,1,2,5,4,6,9,7,10,8}。
第二次交换至此结束。接下来,哨兵j继续向前,发小比6小的3停下来;哨兵i继续向前,发现i==j了!!!于是,这一轮的探测就要结束了,此时交换a[i]与基准的值,数组a就以6为分界线,分成了小于6和大于6的左右两部分:a[10]={3,1,2,5,4,6,9,7,10,8}。  至此,第一轮快速排序完全结束,接下来,对于6左边的半部分3,1,2,5,4,执行以上过程;对于6右边的半部分9,7,10,8,执行以上过程,直到不可拆分出新的子序列为止。最终将会得到这样的序列:1 2 3 4 5 6 7 8 9 10,到此,排序完全结束。
至此,第一轮快速排序完全结束,接下来,对于6左边的半部分3,1,2,5,4,执行以上过程;对于6右边的半部分9,7,10,8,执行以上过程,直到不可拆分出新的子序列为止。最终将会得到这样的序列:1 2 3 4 5 6 7 8 9 10,到此,排序完全结束。 /** * @author:Tokgo J * @date:2019/11/27 * @aim:指针交换法 */public class QuickSort2 { public static void quickSort(int[] arr,int startIndex,int endIndex){ //递归结束条件:startIndex大于等于endIndex的时候 if(startIndex >= endIndex){ return; } //得到基准元素位置 int pivotIndex = partition(arr,startIndex,endIndex); //根据基准元素,分成两部分递归排序 quickSort(arr,startIndex,pivotIndex-1); quickSort(arr,pivotIndex+1,endIndex); } private static int partition(int[] arr,int startIndx,int endIndex){ //取第一个位置的元素作为基准元素 int pivot = arr[startIndx]; int left = startIndx; int right = endIndex; while (left != right){ //控制right指针比较并左移 while (left pivot){ right--; } //控制right指针比较并右移 while (left 发表评论
最新留言
关于作者
