本文共 1212 字，大约阅读时间需要 4 分钟。

欧拉公式：log(n)+y+1.0/(2*n)

欧拉常数y：0.57721566490153286060651209

题：

In mathematics, the nth harmonic number is the sum of the reciprocals of the first n natural numbers:

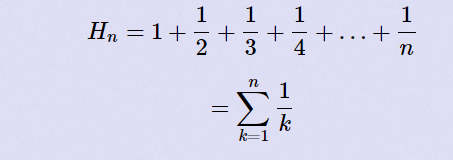
In this problem, you are given n, you have to find Hn.

Input

Input starts with an integer T (≤ 10000), denoting the number of test cases.

Each case starts with a line containing an integer n (1 ≤ n ≤ 10^8).

Output

For each case, print the case number and the nth harmonic number. Errors less than 10^-8 will be ignored.

Sample Input

12 1 2 3 4 5 6 7 8 9 90000000 99999999 100000000

Sample Output

Case 1: 1 Case 2: 1.5 Case 3: 1.8333333333 Case 4: 2.0833333333 Case 5: 2.2833333333 Case 6: 2.450 Case 7: 2.5928571429 Case 8: 2.7178571429 Case 9: 2.8289682540 Case 10: 18.8925358988 Case 11: 18.9978964039 Case 12: 18.9978964139

注：欧拉公式只有在n值大的时候比较准确

#include
   
    #include
    
     using namespace std;const double y=0.57721566490153286060651209;int main(){   	int t,o=0;	double a[10005];	a[1]=1;	for(int i=2;i<=10000;++i)	{   		a[i]=a[i-1]+1.0/i;	}	scanf("%d",&t);	while(t--)	{   		o++;		long n;		double s=0;		scanf("%d",&n);		if(n<10000)		{   			s=a[n];		}		else		{   			s=log(n)+y+1.0/(2*n);		}				printf("Case %d: %.10lf\n",o,s);			}	return 0; }