
大二数据结构(排序)
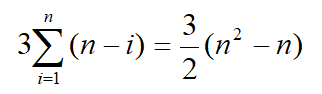
发布日期:2021-05-07 23:24:16
浏览次数:24
分类:精选文章
本文共 4139 字,大约阅读时间需要 13 分钟。
排序
排序
一.概念
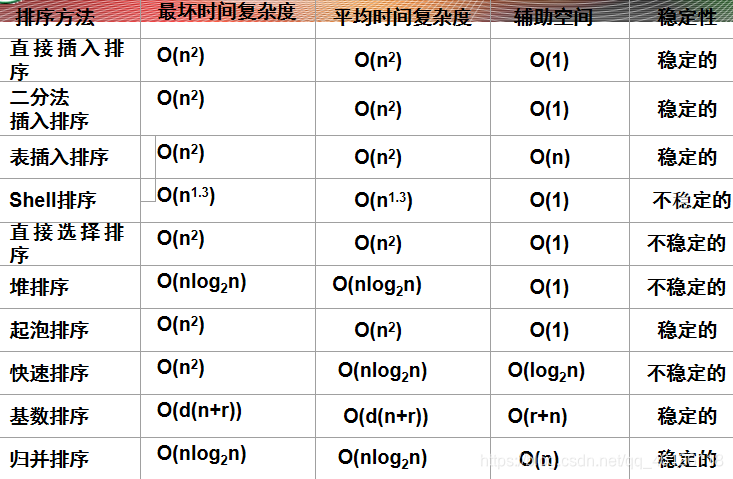
【1】稳定排序和不稳定排序
假设Ki=Kj(0<=i,j<=n-1,i不等于j),且在排序前的序列中Ri领先于Rj(即i<j),若在排序后的序列中Ri仍领先于Rj,则称所用的排序方法是稳定的,否则是不稳定的。
【2】排序分类
- 按待排序记录所在位置
- 内部排序:待排序记录存放在内存
- 外部排序:排序过程中需对外存进行访问的排序
- 按排序依据原则
- 插入排序:直接插入排序、折半插入排序、希尔排序、表插入排序*
- 交换排序:起泡排序、快速排序
- 选择排序:简单选择排序、堆排序
- 归并排序:2-路归并排序
- 分配排序
- 按排序所需工作量
- 简单的排序方法:T(n)=O(n²)
- 先进的排序方法:T(n)=O(logn)
- 排序算法的衡量标准:
- 空间开销:执行算法所需的附加空间
- 时间开销:执行算法所需的时间。通常用算法执行中的比较和移动次数来衡量。考虑最坏和平均情况。
二. 插入排序
【1】直接插入排序
1. 算法
整个排序过程为n-1趟插入,即先将序列中第1个记录看成是一个有序子序列,然后从第2个记录开始,逐个进行插入,直至整个序列有序
typedef struct{ int key; float info;}JD;void straisort(JD r[],int n){ int i,j; for(i=2;i<=n;i++) { r[0]=r[i]; j=i-1; while(r[0].key 2.算法实例

3. 算法评价
- 时间复杂度 T(n)=O(n2)
- 空间复杂度 S(n)=O(1)
【2】二叉法插入
1.算法
void binsort(JD r[],int n){ int i,j,x,s,m,k; for(i=2;i<=n;i++) { r[0]=r[i]; x=r[i].key; s=1; j=i-1; while(s<=j) { m=(s+j)/2; if(x =s;k--) r[k+1]=r[k]; r[s]=r[0]; }} 
2. 算法评价
- 时间复杂度:T(n)=O(n²)
- 空间复杂度:S(n)=O(1)
【3】希尔排序(缩小增量法)
1.算法过程
排序过程:先取一个正整数d1<n,把所有相隔d1的记录放一组,组内进行直接插入排序;然后取d2<d1,重复上述分组和排序操作;直至di=1,即所有记录放进一个组中排序为止。
2. 例子

3.算法
void shellsort(JD r[],int n,int d[T]){ int i,j,k; JD x; k=0; while(k 0)&&(x.key 4.希尔排序特点
- 子序列的构成不是简单的“逐段分割”,而是将相隔某个增量的记录组成一个子序列
- 希尔排序可提高排序速度,因为 :
- 分组后n值减小,n²更小,而T(n)=O(n²),所以T(n)从总体上看是减小了
- 关键字较小的记录跳跃式前移,在进行最后一趟增量为1的插入排序时,序列已基本有序
- 增量序列取法
- 无除1以外的公因子(或者di+1=|_ di/2 _|)
- 最后一个增量值必须为1
三.交换排列
【1】起泡排序
1.排序过程
- 将第一个记录的关键字与第二个记录的关键字进行比较,若为逆序r[1].key>r[2].key,则交换;然后比较第二个记录与第三个记录;依次类推,直至第n-1个记录和第n个记录比较为止——第一趟冒泡排序,结果关键字最大的记录被安置在最后一个记录上
- 对前n-1个记录进行第二趟冒泡排序,结果使关键字次大的记录被安置在第n-1个记录位置
- 重复上述过程,直到“在一趟排序过程中没有进行过交换记录的操作”为止
2. 算法
void bubble_sort(JD r[],int n){ int m,i,j,flag=1; JD x; m=n-1; while((m>0)&&(flag==1)) { flag=0; for(j=1;j<=m;j++) if(r[j].key>r[j+1].key) { flag=1; x=r[j]; r[j]=r[j+1]; r[j+1]=x; } m--; }} 3.算法评价
- 时间复杂度:T(n)=O(n²)
- 最好情况(正序)
- 比较次数:n-1 移动次数:0
- 最坏情况(逆序) 比较次数:
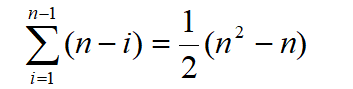
移动次数:
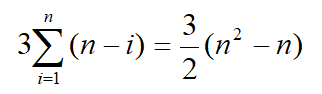
- 空间复杂度:S(n)=O(1)
【2】快速排序
1. 基本思想
通过一趟排序,将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录进行排序,以达到整个序列有序
排序过程:对r[s……t]中记录进行一趟快速排序,附设两个指针i和j,设枢轴记录rp=r[s],x=rp.key- 初始时令i=s,j=t
- 首先从j所指位置向前搜索第一个关键字小于x的记录,并和rp交换
- 再从i所指位置起向后搜索,找到第一个关键字大于x的记录,和rp交换
- 重复上述两步,直至i==j为止
- 再分别对两个子序列进行快速排序,直到每个子序列只含有一个记录为止
2.一个例子

3. 算法
void qksort(JD r[],int t,int w){ int i,j,k; JD x; if(t>=w) return; i=t; j=w; x=r[i]; while(i =x.key)) j--; if(i 4.算法评价
- 时间复杂度 T(n)=O(n²)
- 最好情况(每次总是选到中间值作枢轴)T(n)=O(nlog2n)
- 最坏情况(每次总是选到最小或最大元素作枢轴)T(n)=O(n²)
- 空间复杂度:需栈空间以实现递归
- 最坏情况:S(n)=O(n)
- 一般情况:S(n)=O(log2n)
四. 选择排序
【1】简单选择排序
1. 排序过程
- .首先通过n-1次关键字比较,从n个记录中找出关键字最小的记录,将它与第一个记录交换
- 再通过n-2次比较,从剩余的n-1个记录中找出关键字次小的记录,将它与第二个记录交换
- 重复上述操作,共进行n-1趟排序后,排序结束
2.一个例子

3. 算法
void smp_selesort(JD r[],int n){ int i,j,k; JD x; for(i=1;i 4. 算法评价
-
时间复杂度
-最好情况:0 最坏情况:3(n-1) T(n)=O(n2) -
空间复杂度
-
S(n)=O(1)
【2】堆排序
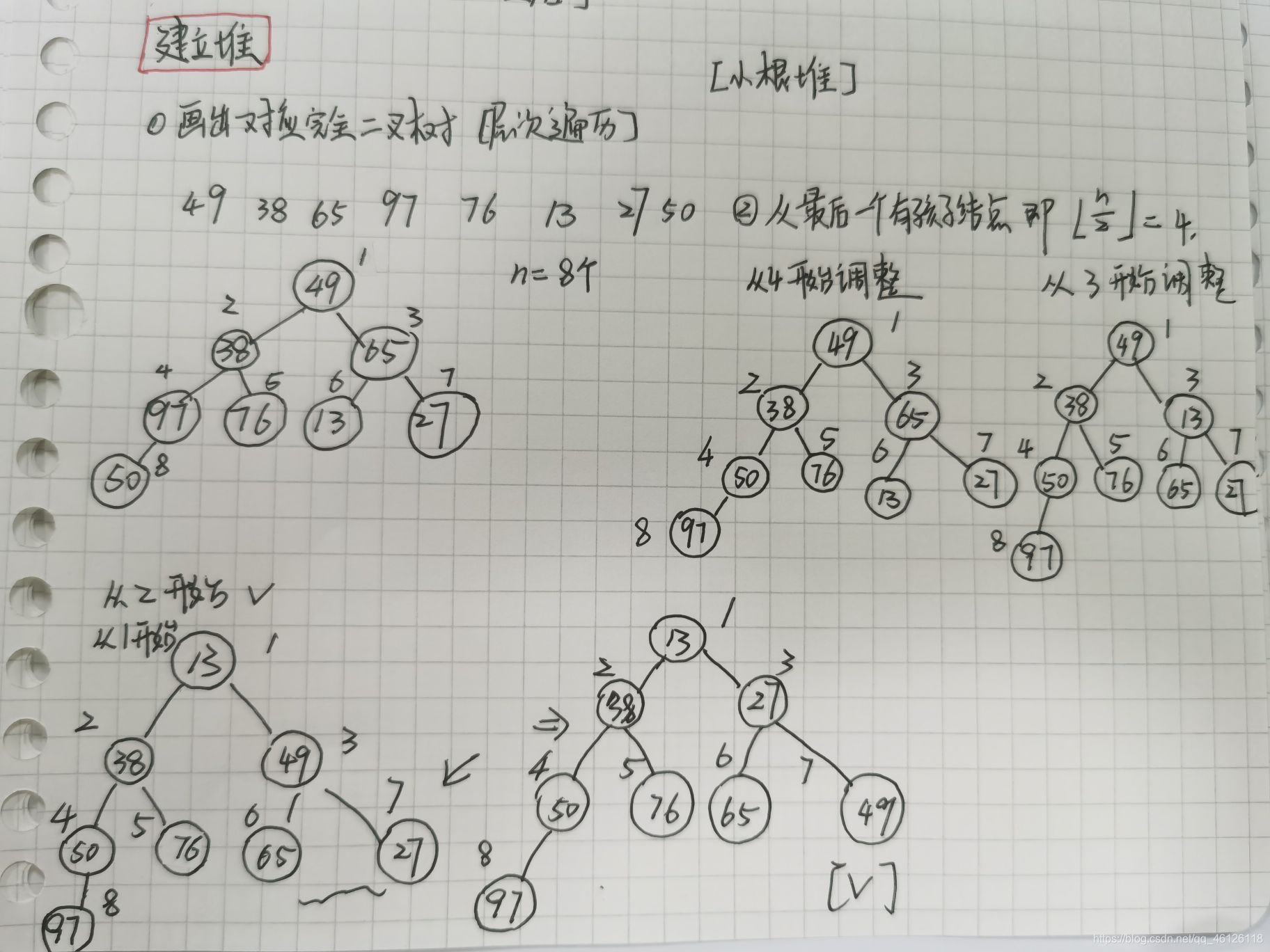
1.建立堆
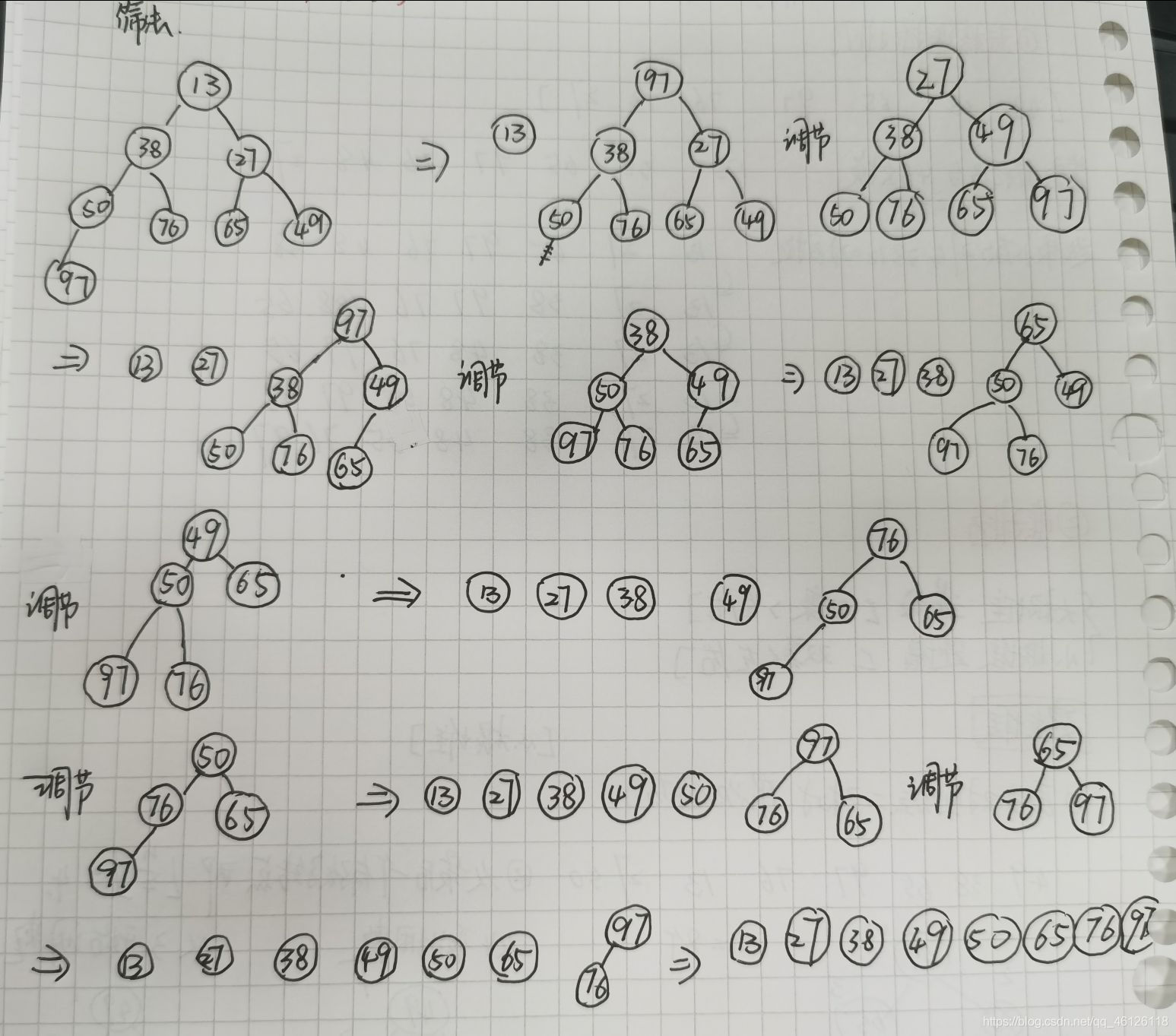
2.排序法
3.算法
void heapsort(JD r[],int n){ int i; JD x; for(i=n/2;i>=1;i--) sift(r,i,n); for(i=n;i>=2;i--) { x=r[1]; r[1]=r[i]; r[i]=x; sift(r,1,i-1); } } int sift(JD r[],int k,int m){ int i,j; JD x; i=k; x=r[i]; j=2*i; while(j<=m) { if((j r[j+1].key)) j++; if(x.key>r[j].key) { r[i]=r[j]; i=j; j=j*2; } else j=m+1; } r[i]=x; } 4.算法评价
- 时间复杂度
- 最坏情况下T(n)=O(nlogn)
- 空间复杂度:
- S(n)=O(1)
五.分配排序
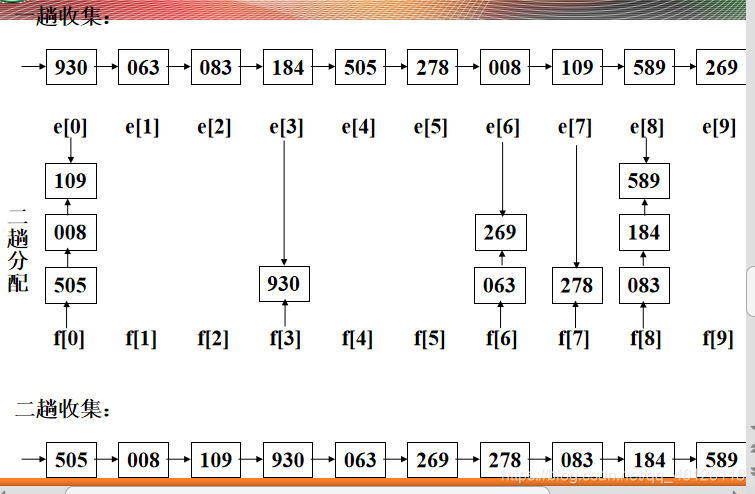
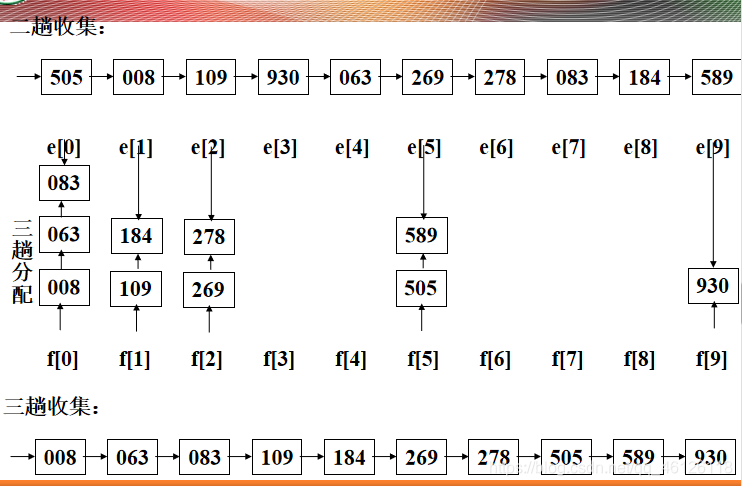
【1】分配排序的思想
把排序码分解成若干部分,然后通过对各个部分排序码的分别排序,最终达到整个排序码的排序
【2】一个例子
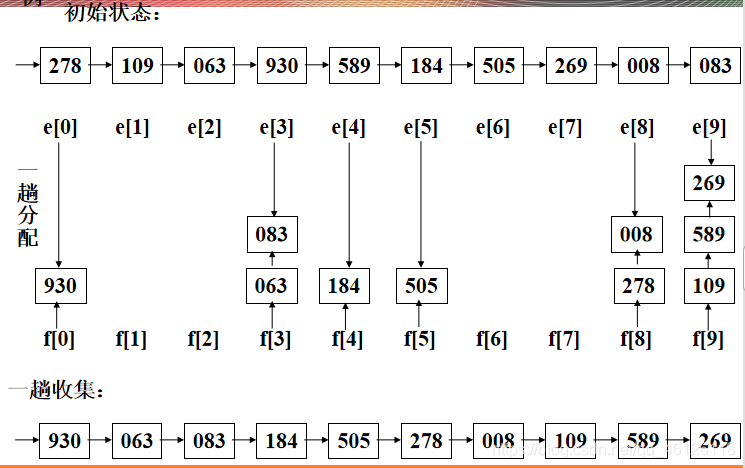


【3】算法评价
- 时间复杂度: T(n)=O(d*(r+n))。
基数排序算法中,时间耗费主要在修改指针上。一趟排序的时间为O(r+n)。总共要进行d趟排序;
当n较大、d较小,特别是记录的信息量较大时,基数排序非常有效。- 空间复杂度: S(n)=O(n+r)。
基数排序中,每个记录中增加了一个next字段,还增加了一个queue数组。
- 基数排序是稳定的。
六.归并排序
【1】排序过程
- 设初始序列含有n个记录,则可看成n个有序的子序列,每个子序列长度为1
- 两两合并,得到n/2个长度为2或1的有序子序列
- 再两两合并,……如此重复,直至得到一个长度为n的有序序列为止
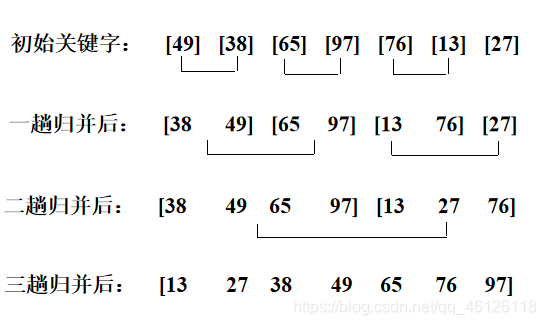
【2】算法评价
时间复杂度:T(n)=O(nlog2n)
空间复杂度:S(n)=O(n)七.总结
发表评论
最新留言
表示我来过!
[***.240.166.169]2025年04月13日 22时27分55秒
关于作者

喝酒易醉,品茶养心,人生如梦,品茶悟道,何以解忧?唯有杜康!
-- 愿君每日到此一游!
推荐文章
js求阶乘
2021-05-08
Nginx---惊群
2021-05-08
项目中常用的审计类型概述
2021-05-08
(九)实现页面底部购物车的样式
2021-05-08
python-day3 for语句完整使用
2021-05-08
基于LabVIEW的入门指南
2021-05-08
weblogic之cve-2015-4852
2021-05-08
Java注释
2021-05-08
C++ 函数重载
2021-05-08
使用mybatis-generator生成底层
2021-05-08
Mybatis【5】-- Mybatis多种增删改查那些你会了么?
2021-05-08
计算输入的一句英文语句中单词数
2021-05-08
lvs+keepalive构建高可用集群
2021-05-08
6 个 Linux 运维典型问题
2021-05-08
取消vim打开文件全是黄色方法
2021-05-08
一个系统部署多个tomcat实例
2021-05-08
HP服务器设置iLO
2021-05-08