本文共 2452 字，大约阅读时间需要 8 分钟。

NOJ-建立二叉树的二叉链表

实则为二叉树的重建

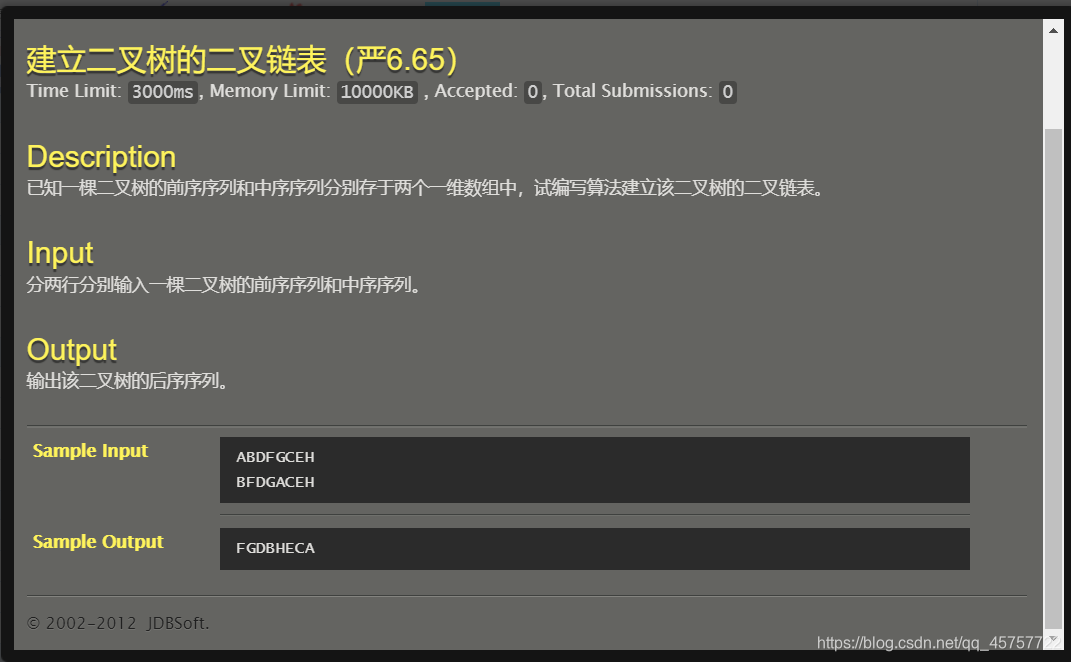
题目分析

输入：一颗二叉树的前序序列和中序序列
输出：一颗二叉树的后序序列。

解题思路

典型的二叉树的重建，如何去重建呢？
二叉树的遍历特点

1. 前序遍历，即是
   1. 访问根结点
   2. 先序遍历左子树
   3. 先序遍历右子树
2. 中序遍历
   1. 中序遍历左子树
   2. 访问根结点
   3. 中序遍历右子树

所以，我们很容易发现
在前序序列中找到的第一个结点就是整棵树的根结点，
而我们要在中序序列找到这个结点就必须遍历完整个左子树。
即：前序序列中找到的根结点，在去中序序列中找到这个结点时
中序序列中出现该元素的位置的左侧，是它的左子树，右侧是它的右子树
从这一基本特点，我们就可以通过递归，从根结点开始，逐次深入，直到叶子结点。

算法执行步骤

1. 创建根结点及其初始化。
2. 判断是否遍历完成，如果完成就返回这个根结点。
3. 设置temp指针记录当前中序序列的首元素的位置。
4. 在中序序列中查找根结点的值所在的位置，并更新I_start的值。
5. 用left来记录第4步中，右移的元素个数，即根结点的左子树元素个数。
6. 递归重建左右子树。

#include<stdio.h>#include<stdlib.h>#include<string.h>typedef struct BiTNode{       char data;    struct BiTNode *lchild, *rchild;//左右孩子指针} BiTNode, *BiTree;void PosOrderTraverse(BiTree T);//后序遍历BiTree Rebuild(char *P_start, char *P_last, char *I_start, char *I_last);//二叉树的重建BiTree Build(char *Ptree, char *Itree,int len);//int main(){       char Ptree[100];    char Itree[100];    int len = 0;    scanf("%s", Ptree);    scanf("%s", Itree);    len = strlen(Ptree);    BiTree T;    T = Build(Ptree, Itree, len);    PosOrderTraverse(T);}void PosOrderTraverse(BiTree T){       if(T->lchild){           PosOrderTraverse(T->lchild);    }    if(T->rchild){           PosOrderTraverse(T->rchild);    }    if(T){           printf("%c", T->data);    }}BiTree Rebuild(char *P_start, char *P_last, char *I_start, char *I_last)//P代表先序序列，I代表中序序列{       BiTree root;    root = (BiTree)malloc(sizeof(BiTNode));//创建一个根节点    root->data = P_start[0];//根节点的值设为前序序列的第一个元素    root->lchild = NULL;    root->rchild = NULL;//清空左右子树    if(P_start==P_last){           if(I_start==I_last&&*P_start==*P_last)        {               return root;//当前序和中序所有元素都被遍历，就返回根节点的值        }    }    char *temp = I_start;//设置一个字符指针去存储当前的中序序列的开始指针    int left = 0;//前序序列中的元素在中序序列中左边的元素个数    while((*I_start!=root->data)&&(I_start<I_last))    {           I_start++;//在中序序列查找到根结点所在位置    }    left = I_start - temp;//左边的元素个数即是目前中序序列start指针减去之前temp所存储的start指针的值    if(left>0){           root->lchild = Rebuild(P_start + 1, P_start + left, temp, I_start - 1);//递归建立左子树    }    //left>0表明左边还有元素说明此根节点可以建立左子树    //此时前序序列P应该向后移动一个位置，并且结束位置在P_start+left这是因为左子树一共有left个元素    //此时中序序列I应从原来的temp遍历到I_start-1，这一段也对应左子树的相应元素。    if(left<(P_last-P_start)){           root->rchild = Rebuild(P_start + left + 1, P_last, I_start + 1, I_last);    }    //右子树的思路同上    return root;}BiTree Build(char *Ptree, char *Itree,int len){       return Rebuild(Ptree, Ptree + len - 1, Itree, Itree + len - 1);}

题外话：最近学习好忙呀，各种考试，图论已经讲了一半了，我还没写图的NOJ，不过得缓一缓，先复习其他科目吧。