本文共 2849 字，大约阅读时间需要 9 分钟。

手写数字识别问题——逻辑回归

一、什么是分类问题？

• 有时我们需要对事物分类（classify）而不是去预测一个具体的数值，例如给定一张含有手写数字（0-9 十个数字中的一个）的图片，我们需要将其分类为 0，1，2，3，4，5，6，7，8，9 十类。
• 或者，我们需要将一首歌曲进行归类，如归类为流行，摇滚，说唱等。集合 [0,1,2，...，9]、[流行，摇滚，说唱，等等] 中的每一个元素都可以表示一个类。在计算机中，我们通常用数字对抽象名词进行表示，比如，pop = 0, rock = 1, 等等。

二、手写数字识别数据集MNIST

• MNIST是机器学习领域的一个经典数据集，包含一系列大小为28x28像素的手写数字灰度图像，分别代表0-9中的一个数字。
  • 训练集 60000
  • 测试集 10000

逻辑回归 Logistic Regression

三、逻辑回归与线性回归的比较

区别:

• 结果（y）：对于线性回归，结果是一个连续的标量值；对于逻辑回归，结果是一个离散整数。
• 特征（x）：对于线性回归，特征都表示为一个列向量；对于涉及二维图像的逻辑回归，特征是一个二维矩阵，矩阵的每个元素表示图像的像素值，每个像素值是属于 0 到 255 之间的整数，其中 0 表示黑色，255 表示白色，其他值表示具有某些灰度阴影。
• 成本函数（成本）：对于线性回归，成本函数是表示每个预测值与其预期结果之间的聚合差异的某些函数；对于逻辑回归，是计算每次预测的正确或错误的某些函数。

相似性

训练：线性回归和逻辑回归的训练目标都是去学习权重（W）和偏置（b）值。

结果：线性回归与逻辑回归的目标都是利用学习到的权重和偏置值去预测/分类结果。

调整

（1）特征 X：

我们可以将二维的图片特征（假设二维特征有 X 行，Y 列）转换成一维的行向量：将第一行以外的其它行数值依顺序放在第一行后面。

• 预测结果 y：
• 真实值应该是类别标签，将其转换为one-hot向量
• 模型输出应该是向量，该向量的每个元素代表逻辑回归模型认为属于某个特定类的得分。
• 具有最高分数的类成为被预测的类。

对于逻辑回归，y 不能作为标量，因为预测可能最终为 2.3 或 11，这不在可能的类 [0,1，...，9] 中。

为了解决这个问题，y 应该被转换成列向量，该向量的每个元素代表逻辑回归模型认为属于某个特定类的得分。在下面的示例中，预测结果为类'1'，因为它具有最高得分。

• 成本函数：交叉熵（cross entropy），信息论中的一个概念，在深度学习中常用于分类问题，衡量预测标签与真实标签之间的差异。
• 从信息量说起
• 假设我们听到了两件事，分别是：
  事件A：巴西队进入了世界杯决赛圈。
  事件B：中国队进入了世界杯决赛圈。
  仅凭直觉来说，显而易见事件B的信息量比事件A的信息量要大。
• 信息量与事件发生的概率有关。
• 因为事件A发生的概率很大，事件B发生的概率很小。所以当越不可能的事件发生了，我们获取到的信息量就越大。越可能发生的事件发生了，我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。

（2）熵 entropy

• 对于某个事件，有n种可能性，每一种可能性都有一个概率p(xi)，这样就可以计算出某一种可能性的信息量。
• 熵用来表示所有信息量的期望

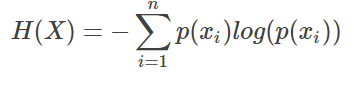
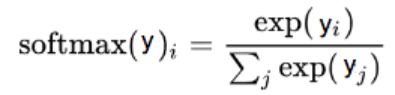
（3）相对熵 （KL散度）

• 如果对于同一个随机变量 x 有两个单独的概率分布 P(x) 和 Q(x)，就可以使用 KL 散度（Kullback-Leibler divergence）来衡量这两个分布的差异。
• 维基百科对相对熵的定义是
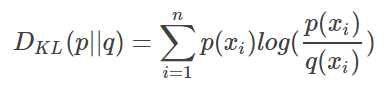
• 即如果用P来描述目标问题，而不是用Q来描述目标问题，得到的信息增量。
• 在机器学习中，P往往用来表示样本的真实分布，比如[1,0,0]表示当前样本属于第一类。Q用来表示模型所预测的分布，比如[0.7,0.2,0.1] 。KL散度越小，表面P和Q越相近。也就是说，模型预测接近于真实分布。
• 直观的理解就是如果用P来描述样本，那么就非常完美。而用Q来描述样本，虽然可以大致描述，但是不是那么的完美，信息量不足，需要额外的一些“信息增量”才能达到和P一样完美的描述。如果我们的Q通过反复训练，也能完美的描述样本，那么就不再需要额外的“信息增量”，Q等价于P。

（4）交叉熵 cross entropy

在机器学习中，我们需要评估label和predicts之间的差距，使用KL散度刚刚好，即DKL(y||y^)DKL(y||y^)，由于KL散度中的前一部分−H(y) 不变，故在优化过程中，只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss。

单分类问题中交叉熵的应用

多分类问题中交叉熵的应用

值得注意的是，这里的Pred不再是通过softmax计算的了，这里采用的是sigmoid。将每一个节点的输出归一化到[0,1]之间。所有Pred值的和也不再为1。换句话说，就是每一个Label都是独立分布的，相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算，每一个节点只有两种可能值，所以是一个二项分布。前面说过对于二项分布这种特殊的分布，熵的计算可以进行简化。

单张样本的loss即为loss=loss猫+loss蛙+loss鼠

（5）softmax

• 为了利用交叉熵，需要将真实标签向量（y）和预测标签向量（y_pred）转换为概率分布
  • 每个类的概率（得分值）在 0-1 之间
  • 所有类的概率（得分值）和必须是 1
• 真实标签向量是one-hot向量，满足上述条件。
• 预测标签向量，需要使用softmax函数进行转换，这里 i 代表类别，比如0, 1, 2, …, 9 十类。

使用公式：

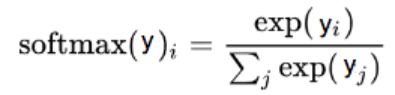
逻辑回归的成本函数：交叉熵

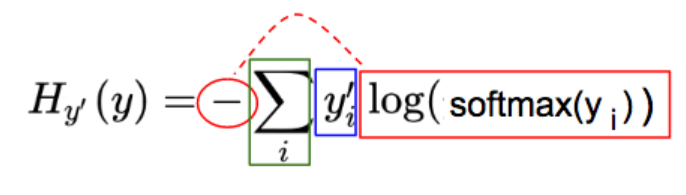
蓝：实际图像类（y'）对应的 one-hot 图

红：由预测向量元素（y）经过softmax(y)，-og(softmax(y）一系列变化而来

绿：每一图片类别 i，其中，i = 0, 1, 2, …, 9, 红蓝部分相乘的结果

逻辑回归的目标是最小化交叉熵（H），这意味着我们只需要最小化 -log（softmax（y_i）项；因为该项与 softmax（y_i）成反比，所以我们实际上是最大化该项。使用反向传播去最小化交叉熵 (H ) 将改变逻辑回归的权重 W 和偏置 b。因此，每张图片的像素值将会给出对应图片类最高分数/概率!（最高分数/概率对应于正确的图片类）

四、TF中实现逻辑回归

1. 将特征变换成一维特征；

2. 将预测结果向量、实际结果向量变化成 one-hot 向量；

3. 将成本函数从平方误差函数变化到交叉熵。

五、总结

• TF代码的基本结构：构建图，会话中执行
• 模型
  • 线性回归——解决连续值的预测问题，属于回归问题
  • 逻辑回归——解决离散标签的预测问题，属于分类问题
• 损失（成本）
  • 回归问题中损失一般用均方误差MSE
  • 分类问题中损失一般用交叉熵
• 梯度下降，最小化损失，求解参数
• 训练数据