本文共 651 字，大约阅读时间需要 2 分钟。

逆合成孔径雷达成像（一）— 傅里叶变换基础1

傅里叶变换是一种非常常见并且实用的数学工具，特别是在分析随机信号，解决先行问题。傅里叶变换可以简单的定义为一个线性算子，目的是将一个域中的函数或者信号映射到另外一个域中以其他形式函数或者信号表示。

在信号与系统中，傅里叶变换常用的方法是将信号从时域变换到频域，或者从频域变换到时域。目的就是为了好算。

1.傅里叶变换公式
傅里叶正变换：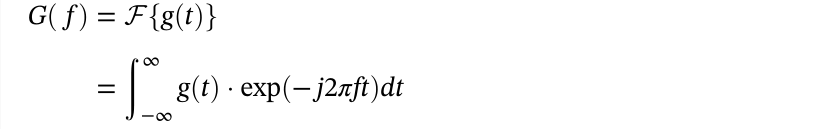
更通俗地来讲，傅里叶变化是把一个信号分解为无穷多个正弦信号或者复指数信号的叠加。
傅里叶反变换:
2.傅里叶变换的常用性质
2.1 线性（同时满足齐次性和叠加性）

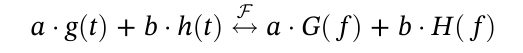
2.2 时域平移

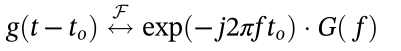
2.3 频域平移

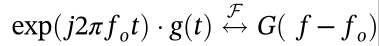
2.4 伸缩变换

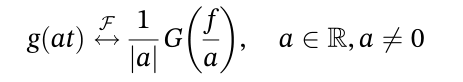
2.5 时域反转

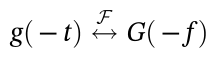
2.6 时域共轭

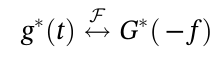
2.7 时域相乘

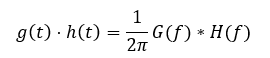
2.8 时域卷积![在这里插入图片描述](https://img-blog.csdnimg.cn/20210503172340907.
2.9 时域微分

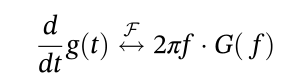
2.10 时域积分

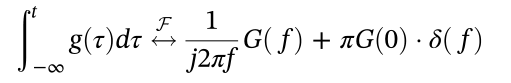
2.11 帕斯瓦尔定理

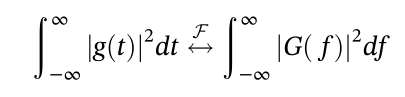
傅里叶变换的概念能够很好地用于平稳信号，但是在真实世界中的信号，其频率内容随时间而变化。为了能够显示这些频率随时间的变化；因此，可以使用joint time–frequency（JTF)来表示。

下一节将详细描述JTF。欢迎关注。

[1] Caner Ozdemir - Inverse Synthetic Aperture Radar Imaging With MATLAB Algorithms-John Wiley & Sons (2021)