本文共 11132 字，大约阅读时间需要 37 分钟。

引言

为什么引入平衡二叉树？

\quad \quad 含有n个结点的二叉排序树的平均查找长度ASL和树的形态有关

问题： 如何提高形态不均衡的二叉排序树的查找效率？

解决办法： 做平衡化处理，尽量让二叉树的形状均衡，转换成平衡二叉树。

1、定义

平衡二叉树（balanced binary tree)

• 又称AVL树（Adelson - VelskII and Landis)。

• 一棵平衡二叉树或者是空树，或者是具有下列性质的二叉排序树：

  • 1）左子树与右子树的高度之差的绝对值小于等于1；
  • 2）左子树与右子树也是平衡二叉树。

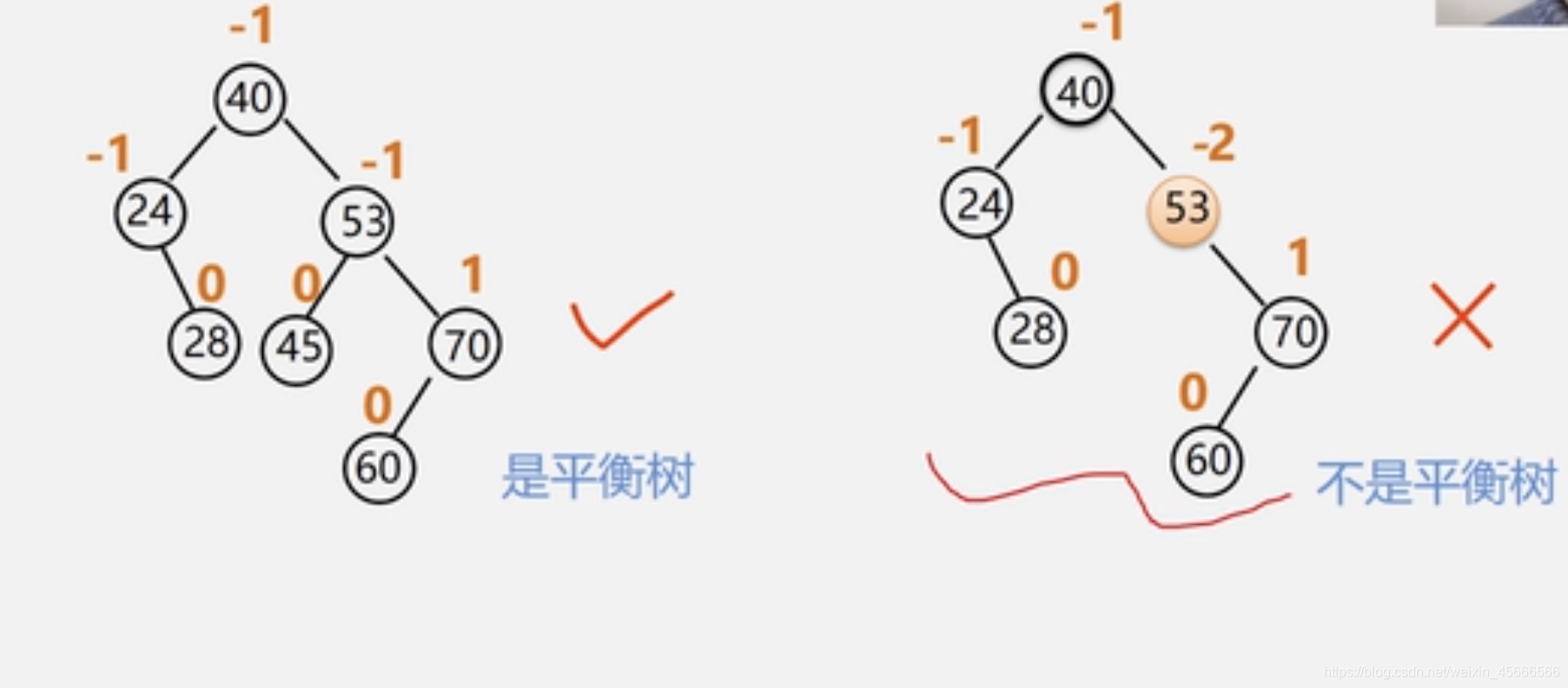
\quad \quad 为了方便起见，给每个结点附加一个数字，给出该结点左子树与右子树的高度差。这个数字称为结点的平衡因子（BF）。

$$平衡因子=结点左子树的高度-结点右子树的高度$$

\quad \quad 根据平衡二叉树的定义，平衡二叉树上所有结点的平衡因子只能是-1、0、1。

\quad \quad 对于一棵有n个结点的AVL树，其高度保持在$O(lo{g}_{2}n)$数量级，ASL也保持在$O(lo{g}_{2}n)$数量级。

2、失衡二叉排序树的分析与调整

\quad \quad 当我们在平衡二叉排序树上插入一个结点时，有可能导致失衡，即出现平衡因子绝对值大于1的结点，如：2、-2。

\quad \quad 如果在一棵AVL树中插入一个新结点后造成失衡，则必须重新调整树的结构，使之恢复平衡。

平衡调整的四种类型

• LL型：LeftLeft，也称“左左”。插入或删除一个节点后，根节点的左孩子（Left Child）的左孩子（Left Child）还有非空节点，导致根节点的左子树高度比右子树高度高2，AVL树失去平衡。左子树高度大于右子树高度

• LR型：LeftRight，也称“左右”。插入或删除一个节点后，根节点的左孩子（Left Child）的右孩子（Right Child）还有非空节点，导致根节点的左子树高度比右子树高度高2，AVL树失去平衡。

• RL型：RightLeft，也称“右左”。插入或删除一个节点后，根节点的右孩子（Right Child）的左孩子（Left Child）还有非空节点，导致根节点的右子树高度比左子树高度高2，AVL树失去平衡。

• RR型：RightRight，也称“右右”。插入或删除一个节点后，根节点的右孩子（Right Child）的右孩子（Right Child）还有非空节点，导致根节点的右子树高度比左子树高度高2，AVL树失去平衡。

如何进行平衡调整的四种类型

\quad \quad AVL树失去平衡之后，可以通过旋转使其恢复平衡。下面分别介绍四种失去平衡的情况下对应的旋转方法。

2.1 LL型—右旋转

\quad \quad 当左子树高度大于右子树高度，应该进行单旋转–右旋转操作:

（1）将根节点的左孩子作为新根节点。

（2）将新根节点的右孩子作为原根节点的左孩子。

（3）将原根节点作为新根节点的右孩子。

【图解过程】：

# 右旋转def right_rotate(node):    if node is None:        return    # 创建新的结点，以当前根结点的值    new_node = copy.deepcopy(node)    # 把新结点的右子树设为当前结点的右子树    new_node.right = node.right    # 把新结点的左子树设为当前结点的左子树的右子树    new_node.left = node.left.right    # 把当前结点的值替换成它的左子结点的值    node.val = node.left.val    # 把当前结点的左子树设置成当前结点的左子树的左子树    node.left = node.left.left    # 把当前结点的右子结点设置成（指向）新的结点    node.right = new_node

2.2 RR型—左旋转

\quad \quad 当右子树高度大于左子树高度，应该进行单旋转–左旋转操作:

(1) 将根节点的右孩子作为新根节点。

(2) 将新根节点的左孩子作为原根节点的右孩子。

(3) 将原根节点作为新根节点的左孩子。

【图解过程】：

• 总体代码都是一样的，只是方向调整一下就可以了

# 左旋转def left_rotate(node):    if node is None:        return    # 创建新的结点，以当前根结点的值    new_node = copy.deepcopy(node) # 这点最重要了，一定是深拷贝，直接赋值是浅拷贝    # --不然下面操作到后面会被置空    # 把新结点的左子树设为当前结点的左子树    new_node.left = node.left    # 把新结点的右子树设为当前结点的右子树的左子树    new_node.right = node.right.left    # 把当前结点的值替换成它的右子结点的值    node.val = node.right.val    # 把当前结点的右子树设置成当前结点的右子树的右子树    node.right = node.right.right    # 把当前结点的左子结点设置成（指向）新的结点    node.left = new_node

2.3 双旋转

\quad \quad 如果它的左子树的右子树的高度 大于 它的左子树的左子树的高度（LR型） 或者它的右子树的左子树的高度 大于 它的右子树的右子树的高度（RL型），不能简单的进行单次的左旋转或者右旋转。见下面例子：

\quad \quad 左图满足右旋转，于是我们进行右旋转，最终7变成了新的根结点，8和9挂到哦了10结点的左边，发现高度差还是大于1，原因是：左边图，8和9 按照二叉排序树的要求，挂在了它的右边，经过调整后，发现都比右边图的10结点小，于是挂在了它的左边，等于没有解决问题！

解决方案：双旋转

1）先得出整体是左边高还是右边高，来进行左旋转或者右旋转；但此时我们不要再先从根结点出发了进行调整了，而是 从 根结点的左右子树高度一侧，将左子树或者右子树当做根结点的一棵新树，先进行一次左旋转或者右旋转；调整后，得到的树，再判断左右子树的高度，此时再从根结点出发，进行左旋转或者右旋转！

2）可以看出，我们开始单一讲的进行左旋转或者右旋转，进行一次，根结点是会发生变化的；而要进行双旋转的树，第一次变化时，根结点没有发生变化，第二次时，才发生变化 3）如下图的调整步骤↓↓↓ 开始的根结点为10 ，对这棵树的根结点的左子树7出发进行一次调整后，整棵树的根结点还是10，只是他的左子树根结点由原来的7变成了8；最后对第一次变化完的数，从根结点出发，根结点发生变化，由原来的10变成了8 ！

2.3.1 LR型—双旋转—先左旋后右旋

\quad \quad 当它的左子树的右子树的高度 大于 它的左子树的左子树的高度（LR型）且左子树高度大于右子树高度（差值>1)时，对二叉树先左旋，再右旋。

(1) 围绕根节点的左孩子进行RR旋转即左旋转。

(2) 围绕根节点进行LL旋转即右旋转。

【图解过程】

2.3.2 RL型—双旋转—先右旋后左旋

\quad \quad 当它的右子树的左子树的高度 大于 它的右子树的右子树的高度（RL型）且右子树高度大于左子树高度(差值>1)时，对二叉树先右旋，再左旋。

(1) 围绕根节点的右孩子进行LL旋转即右旋转。

(2) 围绕根节点进行RR旋转即左旋转。

【图解过程】

注：从这四种旋转可以看出，首先我们应该判断树是LL、RR、LR、RL？然后对于LL就进行右旋转一次，对于RR就进行左旋转一次，对于LR先进行内旋转（也就是左旋转）再进行外旋转（也就是右旋转），对于RL同样是先进行内旋转（也就是右旋转），然后进行外旋转（也就是左旋转）然后就把树转化成了平衡树。

3、构造平衡二叉树

\quad \quad 构造平衡二叉树跟构造搜索二叉树差不多，只不过在每插入一个结点时，需要判断是否失衡，如果失衡，则需要调整

3.1 例子

\quad \quad 输入关键字序列（16，3，7，11，9，26，18，14，15），给出构造一棵AVL树的步骤。

• AVL树构造完毕

3.2python实现AVL树

1、判断是否平衡？—计算 二叉树 左右子树以及树 的高度

\quad \quad 条件：左子树与右子树的高度之差的绝对值小于等于1；

\quad \quad 需求：需要计算左右子树以及树的高度

class TreeNode(object):    def __init__(self, val):        self.val = val        self.left = None        self.right = Noneclass AVLTree(object):    def __init__(self):        self.root = None    # 返回左子树的高度    def left_height(self, node): # 开始传入根结点，后面传入每颗子树的根结点        if node is None:            return 0        return self.tree_height(node.left)    # 返回右子树的高度    def right_height(self, node): # 开始传入根结点，后面传入每颗子树的根结点        if node is None:            return 0        return self.tree_height(node.right)    # 返回以该结点为根结点的树的高度    def tree_height(self, node):         if node is None:            return 0        return max(self.tree_height(node.left), self.tree_height(node.right)) + 1 # 注意加1    # 添加结点    def add(self, val):        node = TreeNode(val)        if self.root is None:            self.root = node            return        queue = [self.root]        while queue:            temp_node = queue.pop(0)            # 判断传入结点的值和当前子树结点的值关系            if node.val < temp_node.val:                if temp_node.left is None:                    temp_node.left = node                    return                else:                    queue.append(temp_node.left)            if node.val >= temp_node.val:                if temp_node.right is None:                    temp_node.right = node                    return                else:                    queue.append(temp_node.right)    '''    也可以用递归实现添加结点，记得传入根结点    def add(self, root, val):        node = TreeNode(val)        if root is None:            self.root = node            return        if val < root.val:            if not root.left:                root.left = node                return            else:                self.add(root.left, val)        else:            if not root.right:                root.right = node                return            else:                self.add(root.right, val)    '''        	# 中序遍历测试    def in_order(self, node):        if node is None:            return        self.in_order(node.left)        print(node.val, end=" ")        self.in_order(node.right)if __name__ == '__main__':    a = AVLTree()    node_array = [4, 3, 6, 5, 7, 8]    for item in node_array:        # a.add(a.root, item) 递归添加结点时用        a.add(item)    print("中序遍历结果为：")    a.in_order(a.root)     print()    print("树的高度为:", a.tree_height(a.root))     print("左子树高度为：", a.left_height(a.root))     print("右子树高度为：", a.right_height(a.root))     ''' 输出结果为：中序遍历结果为：3 4 5 6 7 8 树的高度为: 4左子树高度为： 1右子树高度为： 3'''

2、定义左旋转、右旋转并实现平衡二叉树

import copyclass TreeNode(object):    def __init__(self, val):        self.val = val        self.left = None        self.right = Noneclass AVLTree(object):    def __init__(self):        self.root = None    # 返回左子树的高度    def left_height(self, node):  # 开始传入根结点，后面传入每颗子树的根结点        if node is None:            return 0        return self.tree_height(node.left)    # 返回右子树的高度    def right_height(self, node):  # 开始传入根结点，后面传入每颗子树的根结点        if node is None:            return 0        return self.tree_height(node.right)    # 返回以该结点为根结点的树的高度    def tree_height(self, node):        if node is None:            return 0        return max(self.tree_height(node.left), self.tree_height(node.right)) + 1    # 进行左旋转    def left_rotate(self, node):        if node is None:            return        # 创建新的结点，以当前根结点的值        new_node = copy.deepcopy(node)        # 把新结点的左子树设为当前结点的左子树        new_node.left = node.left        # 把新结点的右子树设为当前结点的右子树的左子树        new_node.right = node.right.left        # 把当前结点的值替换成它的右子结点的值        node.val = node.right.val        # 把当前结点的右子树设置成当前结点的右子树的右子树        node.right = node.right.right        # 把当前结点的左子结点设置成（指向）新的结点        node.left = new_node    # 进行右旋转    def right_rotate(self, node):        if node is None:            return        # 创建新的结点，以当前根结点的值        new_node = copy.deepcopy(node)        # 把新结点的右子树设为当前结点的右子树        new_node.right = node.right        # 把新结点的左子树设为当前结点的左子树的右子树        new_node.left = node.left.right        # 把当前结点的值替换成它的左子结点的值        node.val = node.left.val        # 把当前结点的左子树设置成当前结点的左子树的左子树        node.left = node.left.left        # 把当前结点的右子结点设置成（指向）新的结点        node.right = new_node    # 添加结点    def add(self, val):        node = TreeNode(val)        if self.root is None:            self.root = node            return        queue = [self.root]        while queue:            temp_node = queue.pop(0)            # 判断传入结点的值和当前子树结点的值关系            if node.val < temp_node.val:                if temp_node.left is None:                    temp_node.left = node                    return                else:                    queue.append(temp_node.left)            if node.val >= temp_node.val:                if temp_node.right is None:                    temp_node.right = node                    return                else:                    queue.append(temp_node.right)    '''    # 递归添加结点    def add(self, root, val):        node = TreeNode(val)        if root is None:            self.root = node            return        if val < root.val:            if not root.left:                root.left = node                return            else:                self.add(root.left, val)        else:            if not root.right:                root.right = node                return            else:                self.add(root.right, val)    '''    def jude_node(self, node):  # 判断二叉排序树是否需要调整（是否达到平衡）        if self.right_height(node) - self.left_height(node) > 1:  # 右子树高于左子树            # 如果它的右子树的左子树的高度 大于 它的右子树的右子树高度            if node.right and self.left_height(node.right) > self.right_height(node.right):                # 先对当前结点的右子结点（右子树）进行-> 右旋转                self.right_rotate(node.right)                # 再对当前结点进行左旋转                self.left_rotate(self.root)            else:                # 直接进行左旋转                self.left_rotate(self.root)            return # 注意这个return 因为判断为一种情况，就要总结判断        if self.left_height(node) - self.right_height(node) > 1:  # 左子树高于右子树            # 如果它的左子树的右子树的高度 大于 它的左子树的左子树的高度            if node.left and self.right_height(node.left) > self.left_height(node.left):                # 先对当前结点的左子结点（左子树）进行-> 左旋转                self.left_rotate(node.left)                # 再对当前结点进行右旋转                self.right_rotate(self.root)            else:                # 直接进行右旋转                self.right_rotate(self.root)    # 中序遍历测试    def in_order(self, node):        if node is None:            return        self.in_order(node.left)        print(node.val, end=" ")        self.in_order(node.right)    # 前序遍历测试（主要看根结点的变化）    def pre_order(self, node):        if node is None:            return        print(node.val, end=" ")        self.pre_order(node.left)        self.pre_order(node.right)if __name__ == '__main__':    a = AVLTree()    # 测试左旋转结点值数组    # node_array = [4, 3, 6, 5, 7, 8]    # 测试右旋转结点值数组    # node_array = [10, 12, 8, 9, 7, 6]    # 测试双旋转结点数组    node_array = [10, 11, 7, 6, 8, 9]    for item in node_array:        # a.add(a.root, item)        a.add(item)    a.jude_node(a.root)    print("中序遍历结果为：")    a.in_order(a.root)    print()    print("旋转后，前序遍历结果为：")    a.pre_order(a.root)    print()    print("树的高度为:", a.tree_height(a.root))    print("左子树高度为：", a.left_height(a.root))    print("右子树高度为：", a.right_height(a.root))''' 输出结果中序遍历结果为：6 7 8 9 10 11 旋转后，前序遍历结果为：8 7 6 10 9 11 树的高度为: 3左子树高度为： 2右子树高度为： 2'''

参考资料：

1、https://blog.csdn.net/qq_25343557/article/details/89110319 2、相关视频 3、https://blog.csdn.net/qq_21993785/article/details/80576642