本文共 2132 字，大约阅读时间需要 7 分钟。

一、内存分配中的堆栈

从静态存储区域分配：它是由编译器自动分配和释放的，即内存在程序编译的时候就已经分配好，这块内存在程序的整个运行期间都存在，直到整个程序运行结束时才被释放，如全局变量与 static 变量。

在栈上分配：它同样也是由编译器自动分配和释放的，即在执行函数时，函数内局部变量的存储单元都可以在栈上创建，函数执行结束时这些存储单元将被自动释放。需要注意的是，栈内存分配运算内置于处理器的指令集中，它的运行效率一般很高，但是分配的内存容量有限。

从堆上分配：也被称为动态内存分配，它是由程序员手动完成申请和释放的。即程序在运行的时候由程序员使用内存分配函数（如 malloc 函数）来申请任意多少的内存，使用完之后再由程序员自己负责使用内存释放函数（如 free 函数）来释放内存。也就是说，动态内存的整个生存期是由程序员自己决定的，使用非常灵活。需要注意的是，如果在堆上分配了内存空间，就必须及时释放它，否则将会导致运行的程序出现内存泄漏等错误。

2、区别

内存分配中的栈与堆主要存在如下区别：

1) 分配与释放方式

栈

栈内存是由编译器自动分配与释放的，它有两种分配方式：静态分配和动态分配。

静态分配是由编译器自动完成的，如局部变量的分配（即在一个函数中声明一个 int 类型的变量i时，编译器就会自动开辟一块内存以存放变量 i）。与此同时，其生存周期也只在函数的运行过程中，在运行后就释放，并不可以再次访问。

动态分配由 alloca 函数进行分配，但是栈的动态分配与堆是不同的，它的动态分配是由编译器进行释放，无需任何手工实现。值得注意的是，虽然用 alloca 函数可以实现栈内存的动态分配，但 alloca 函数的可移植性很差，而且在没有传统堆栈的机器上很难实现。因此，不宜使用于广泛移植的程序中。当然，完全可以使用 C99 中的变长数组来替代 alloca 函数。

堆

而堆内存则不相同，它完全是由程序员手动申请与释放的，程序在运行的时候由程序员使用内存分配函数（如 malloc 函数）来申请任意多少的内存，使用完再由程序员自己负责使用内存释放函数（如 free 函数）释放内存

2) 分配的碎片问题

对堆来说，频繁分配和释放（malloc / free）不同大小的堆空间势必会造成内存空间的不连续，从而造成大量碎片，导致程序效率降低；而对栈来讲，则不会存在这个问题

3) 分配的效率

大家都知道，栈是机器系统提供的数据结构，计算机会在底层对栈提供支持，例如，分配专门的寄存器存放栈的地址，压栈出栈都有专门的执行指令，这就决定了栈的效率比较高。一般而言，只要栈的剩余空间大于所申请空间，系统就将为程序提供内存，否则将报异常提示栈溢出。

4) 申请的大小限制

由于操作系统是用链表来存储空闲内存地址（内存区域不连续）的，同时链表的遍历方向是由低地址向高地址进行的。因此，堆内存的申请大小受限于计算机系统中有效的虚拟内存。

而栈则不同，它是一块连续的内存区域，其地址的增长方向是向下进行的，向内存地址减小的方向增长。由此可见，栈顶的地址和栈的最大容量一般都是由系统预先规定好的，如果申请的空间超过栈的剩余空间时，将会提示溢出错误。由此可见，相对于堆，能够从栈中获得的空间相对较小。

而堆则不同，它是由 C/C++ 函数库提供的，它的机制也相当复杂。例如，为了分配一块堆内存，首先应该知道操作系统有一个记录空闲内存地址的链表，当系统收到程序的申请时，会遍历该链表，寻找第一个空间大于所申请空间的堆节点，然后将该节点从空闲节点链表中删除，并将该节点的空间分配给程序。而对于大多数系统，会在这块内存空间的首地址处记录本次分配的大小，这样，代码中的 delete 语句才能正确释放本内存空间。另外，由于找到的堆节点的大小不一定正好等于申请的大小，系统会自动将多余的那部分重新放入空闲链表中。很显然，堆的分配效率比栈要低得多。

二、数据结构中的堆栈

数据结构的堆和栈

在实际编程中，可以通过两种方式来实现：使用数组的形式来实现栈，这种栈也称为静态栈；使用链表的形式来实现栈，这种栈也称为动态栈。

相对于栈的“先进后出”特性，堆则是一种经过排序的树形数据结构，常用来实现优先队列等。假设有一个集合 K={k0，k1，…，kn-1}，把它的所有元素按完全二叉树的顺序存放在一个数组中，并且满足：

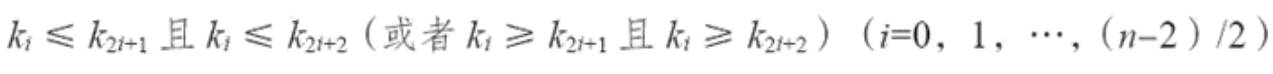
则称这个集合 K 为最小堆（或者最大堆）。

由此可见，堆是一种特殊的完全二叉树。其中，节点是从左到右填满的，并且最后一层的树叶都在最左边（即如果一个节点没有左儿子，那么它一定没有右儿子）；每个节点的值都小于（或者都大于）其子节点的值。