本文共 5154 字，大约阅读时间需要 17 分钟。

作为数据结构的课程笔记，以便查阅。如有出错的地方，还请多多指正！

注：C++忘得太厉害了。。算法先用C实现，等之后复习了再改成C++

• 有向无环图 / DAG图(directed acycline graph)

拓扑排序 Topological Sort

问题提出：学生选修课程问题
学生应按怎样的顺序学习这些课程，才能无矛盾、顺利地完成学业？

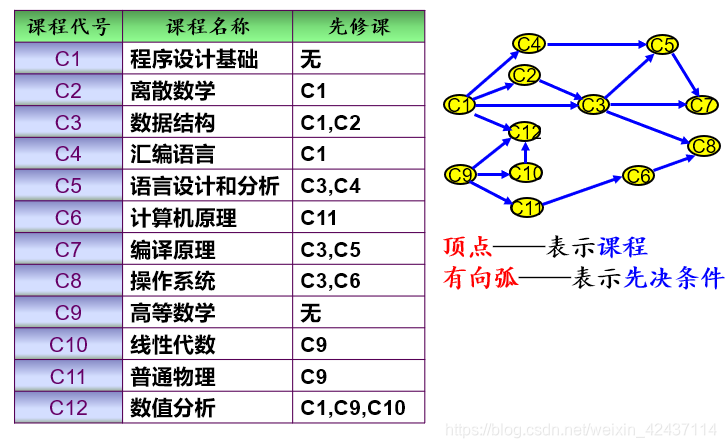
• AOV网——用顶点表示活动，用弧表示活动间优先关系的有向图称为顶点表示活动的网(Activity On Vertex network)
  AOV网中不允许有回路，这意味着某项活动以自己为先决条件
• 拓扑排序——把AOV网络中各顶点按照它们相互之间的优先关系排列成一个线性序列

拓扑排序的方法

• 在有向图中选一个没有前驱的顶点且输出之
• 从图中删除该顶点和所有以它为尾的弧
• 重复上述两步，直至全部顶点均已输出；或者当图中不存在无前驱的顶点为止
  

检测AOV网中是否存在环方法：对有向图构造其顶点的拓扑有序序列，若网中所有顶点都在它的拓扑有序序列中，则该AOV网必定不存在环

算法实现

拓扑排序中，最常用的操作就是求邻接点和入度。因此以邻接表作为存储结构

• 额外设置一个数组来存储各个结点的入度，或者加入入度域
  
• 邻接表中所有入度为0的顶点进栈
• 栈非空时，栈顶元素$V$出栈并输出到拓扑序列中；将$V$的所有邻接顶点入度减1，若为0则进栈
  重复上述操作直至栈空为止
• 若栈空时输出的顶点个数不是$n$，则有向图有环；否则，拓扑排序完毕
  
  输出序列：6 1 3 2 4 5

static void Calc_indegree(pAdjacentList_t pgraph, int indegree[]){   	for (int i = 0; i < pgraph->vexNum; ++i)	{   		indegree[i] = 0;	}	for (int i = 0; i < pgraph->vexNum; ++i)	{   		pArcNode_t arc;		for (arc = pgraph->vex[i].firstEdge; arc; arc = arc->nextEdge)		{   			indegree[arc->head]++;		}	}}//拓扑排序int Topological_sort(pAdjacentList_t pgraph, void (*visit)(AdjacentListDataType_t data)){   	int* indegree = (int*)malloc(pgraph->vexNum * sizeof(int));	pStackNode_t ptop;	int cnt = 0;//输出的顶点个数	Calc_indegree(pgraph, indegree);	Stack_init(&ptop);	for (int i = 0; i < pgraph->vexNum; ++i)	{   		if (0 == indegree[i])		{   			Push(&ptop, i);		}	}		while (!Stack_is_empty(ptop))	{   		int i;		pArcNode_t arc;		Pop(&ptop, &i);		visit(pgraph->vex[i].data);		++cnt;		for (arc = pgraph->vex[i].firstEdge; arc; arc = arc->nextEdge)		{   			if (0 == --indegree[arc->head])			{   				Push(&ptop, arc->head);			}		}	}	free(indegree);	return (cnt == pgraph->vexNum);//是否有环}

$$T(n)=O(n+e)$$

关键路径 Critical Path

问题提出

设一个工程有11项活动，9个事件
问题：(1) 完成整项工程至少需要多少时间？ (2) 哪些活动是影响工程进度的关键？

把工程计划表示为有向图。每个事件表示在它之前的活动已完成，在它之后的活动可以开始

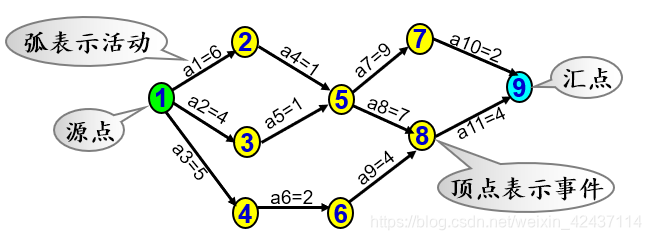
只有在不改变关键路径的前提下，提高所有关键路径上的公共活动的效率才能缩短整个工期

基本概念

• 完成整个工程的最短时间为：从有向图的源点到汇点的最长路径
• AOE网(Activity On Edge)。AOE网中顶点表示事件，弧表示活动，权表示活动持续时间
• 关键路径——路径长度最长的路径
• $V_e(j)$——表示事件$V_j$的最早发生时间
• $V_l(j)$——表示事件$Vj$的最迟发生时间（不影响工期）
• $e(i)$——表示活动$a_i$的最早开始时间
• $l(i)$——表示活动$a_i$的最迟开始时间（不影响工期）
• $l(i)-e(i)$——表示完成活动$a_i$的时间余量
• 关键活动——$l(i)=e(i)$的活动，由关键活动组成关键路径

问题分析

• 如何找$e(i)=l(i)$的关键活动？
  设活动$a_i$用弧$<j,k>$表示，其持续时间记为：$dut(<j,k>)$
  则有：$e(i)=V_e(j)$ ，$l(i)=V_l(k)-dut(<j,k>)$

• 如何求$V_e(j)$和$V_l(j)$？
  (1) 从$V_e(1)=0$开始从前向后递推(拓扑有序)
  
  (2)从$V_l(n)=V_e(n)$开始从后向前递推(逆拓扑有序)
  

• 求关键路径步骤
  求$V_e(i)$
  求$V_l(j)$
  求$e(i)=V_e(j)$
  求$l(i)=V_l(k)-dut(<j,k>)$
  计算$l(i)-e(i)$

算法实现

• 使用邻接表，增设入度域(或者一个记录各个结点入度的数组)
• 计算每个顶点的入度
• 对各个顶点进行拓扑排序，排序过程中求$V_e(i)$。将得到的拓扑序列入栈，以便之后得到逆拓扑序列
• 按逆拓扑序列求$V_l(i)$
• 计算每条弧（活动）的$e[i]$和$l[i]$,找出$e[i]=l[i]$的关键活动

//求图上的关键路径Status_e Critical_path(pAdjacentList_t pgraph){   	int* indegree = (int*)malloc(pgraph->vexNum * sizeof(int));	AdjacentListWeightType_t* ve = (AdjacentListWeightType_t*)malloc(pgraph->vexNum * sizeof(AdjacentListWeightType_t));	AdjacentListWeightType_t* vl = (AdjacentListWeightType_t*)malloc(pgraph->vexNum * sizeof(AdjacentListWeightType_t));	AdjacentListWeightType_t ee;	AdjacentListWeightType_t el;	pStackNode_t ptop;	int cnt = 0;//输出的顶点个数	pStackNode_t ptop_topological;//记录拓扑排序的次序 方便之后按逆序操作	int finish_time = 0;		Calc_indegree(pgraph, indegree);	Stack_init(&ptop);	Stack_init(&ptop_topological);	//入度为0的点入栈	for (int i = 0; i < pgraph->vexNum; ++i)	{   		if (0 == indegree[i])		{   			Push(&ptop, i);		}		ve[i] = 0;		vl[i] = INFINITY;	}	//栈不为空时，拓扑排序	while (!Stack_is_empty(ptop))	{   		int i;		pArcNode_t arc;		Pop(&ptop, &i);		Push(&ptop_topological, i);		++cnt;		for (arc = pgraph->vex[i].firstEdge; arc; arc = arc->nextEdge)		{   			ve[arc->head] = MAX(ve[i] + arc->weight, ve[arc->head]);			if (0 == --indegree[arc->head])			{   				Push(&ptop, arc->head);			}			finish_time = MAX(finish_time, ve[arc->head]);		}	}	if (cnt < pgraph->vexNum)	{   		printf("There is loop in the graph!\r\n");		return err;	}	else {   		printf("Project time:%d\n", finish_time);	}	while (!Stack_is_empty(ptop_topological))	{   		int i;		pArcNode_t arc;		Pop(&ptop_topological, &i);		arc = pgraph->vex[i].firstEdge;		if (NULL == arc)		{   			vl[i] = finish_time;		}		for (; arc; arc = arc->nextEdge)		{   			vl[i] = MIN(vl[arc->head] - arc->weight, vl[i]);		}	}	printf("Critical path:\r\n");	for (int i = 0; i < pgraph->vexNum; ++i)	{   		pArcNode_t arc;		for (arc = pgraph->vex[i].firstEdge; arc; arc = arc->nextEdge)		{   			ee = ve[i];			el = vl[arc->head] - arc->weight;			if (ee == el)			{   				printf("%d -> %d ( weight: %d ; ee/el : %d )\r\n", i, arc->head, arc->weight, ee);			}		}	}	free(indegree);	free(ve);	free(vl);	return ok;}

$$T(n)=O(n+e)$$