线性回归模型属于经典的统计学模型，该模型的应用场景是根据已知的变量(自变量)来预测某个连续的数值变量(因变量)。

一元线性回归模型：y=a+bx+ε

import pandas as pdimport matplotlib.pyplot as pltimport seaborn as snsf = open(r'C:\Users\active\Music\Desktop\Python\第7章 线性回归模型\第7章 线性回归模型\第七章 线性回归模型\Salary_Data.csv', encoding='UTF-8')income = pd.read_csv(f)sns.lmplot(x='YearsExperience',y='Salary',data=income,ci=None)plt.show()

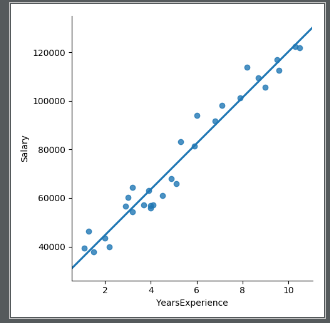
如何得到这条拟合线数学表达式？

运用statsmodels，用于统计建模的第三方模块，如需实现线性回归模型的参数求解，可以调用子模块中的ols函数。有关该函数的语法及参数含义如下

formula：以字符串的形式指定线性回归模型的公式，如‘y~x’就表示简单线性回归模型。

data：指定建模的数据集。

subset：通过bool类型数组对象，获取data的子集用于建模。

drop_cols:指定需要从data中删除的变量。

import statsmodels.api as smfit = sm.formula.ols('Salary~YearsExperience',data=income).fit()print(fit.params)OUT:Intercept          25792.200199YearsExperience     9449.962321dtype: float64

 多元线性回归模型：y=y=β0+β1x1+β2x2+...+ε

回归模型参数的求解：最小二乘法

回归模型的预测：用predict方法(predict(exog=None，transform=True)

exog：指定用于预测的用于预测的其他自变量的值

transform：bool类型参数，预测时是否将原始数据按照模型表达式进行转换，默认为True

接下来将基于statsmodels模块对多元线性回归模型的参数进行求解，进而依据其他新的自变量值实现模型的预测功能。