本文共 3094 字，大约阅读时间需要 10 分钟。

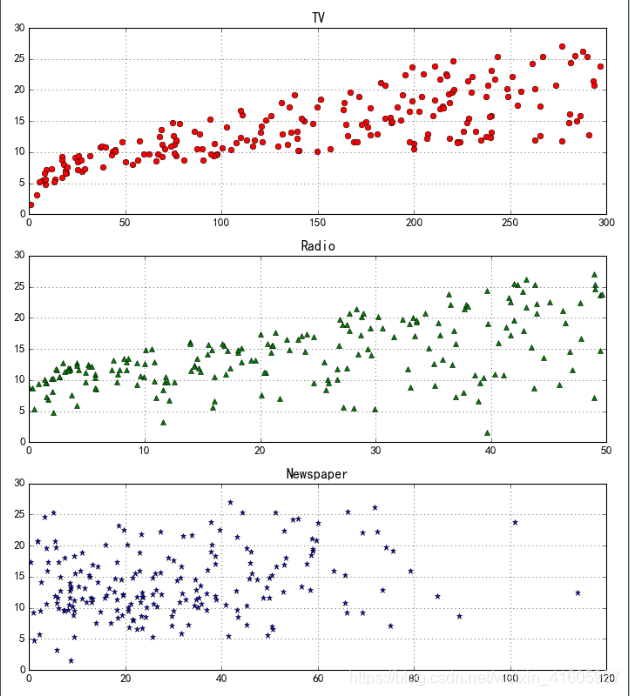
#导入相关的包import numpy as npimport matplotlib as mplimport matplotlib.pyplot as pltimport pandas as pdfrom sklearn.model_selection import train_test_splitfrom sklearn.linear_model import LinearRegressionif __name__ == "__main__":    path = 'Advertising.csv'#文件的路径    # pandas读入    data = pd.read_csv(path)  # TV、Radio、Newspaper、Sales    x = data[['TV', 'Radio', 'Newspaper']]    #x = data[['TV', 'Radio']]    y = data['Sales']    mpl.rcParams['font.sans-serif'] = [u'simHei']    mpl.rcParams['axes.unicode_minus'] = False    # 绘制1    plt.figure(facecolor='w')    plt.plot(data['TV'], y, 'ro', label='TV')    plt.plot(data['Radio'], y, 'g^', label='Radio')    plt.plot(data['Newspaper'], y, 'mv', label='Newspaer')    plt.legend(loc='lower right')    plt.xlabel(u'广告花费', fontsize=16)    plt.ylabel(u'销售额', fontsize=16)    plt.title(u'广告花费与销售额对比数据', fontsize=20)    plt.grid()    plt.show()    # 绘制2右下角的那个小的图框    plt.figure(facecolor='w', figsize=(9, 10))    plt.subplot(311)    plt.plot(data['TV'], y, 'ro')    plt.title('TV')    plt.grid()    plt.subplot(312)    plt.plot(data['Radio'], y, 'g^')    plt.title('Radio')    plt.grid()    plt.subplot(313)    plt.plot(data['Newspaper'], y, 'b*')    plt.title('Newspaper')    plt.grid()    plt.tight_layout()    plt.show()    x_train, x_test, y_train, y_test = train_test_split(x, y, train_size=0.8, random_state=1)#这里使用了函数的交叉验证集的问题80%的测试20%的验证集    print(type(x_test))    print("x_train.shape=",x_train.shape,"y_train.shape=", y_train.shape)    linreg = LinearRegression()# 使用线性回归模型    #linreg = Lasso()    """#另一种数据降维方法，该方法不仅适用于线性情况，也适用于非线性情况。Lasso是      基于惩罚方法对样本数据进行变量选择，通过对原本的系数进行压缩，将原本很小的系数直接压缩至0，从而将这部分系数所对应的变量视为非显著性变量，将不显著的变量直接舍弃。"""    #linreg = Ridge()#使用的是岭回归模型    model = linreg.fit(x_train, y_train)    print("model=",model)    print("linreg.coef_",linreg.coef_,"linreg.intercept_",linreg.intercept_)#输出了系数矩阵    order = y_test.argsort(axis=0)#argsort()函数是将x中的元素从小到大排列    y_test = y_test.values[order]    x_test = x_test.values[order, :]    y_hat = linreg.predict(x_test)    mse = np.average((y_hat - np.array(y_test)) ** 2)  # Mean Squared Error    rmse = np.sqrt(mse)  # Root Mean Squared Error    print('MSE = ', mse, )    print('RMSE = ', rmse)    print('R2 = ', linreg.score(x_train, y_train))    print('R2 = ', linreg.score(x_test, y_test))    plt.figure(facecolor='w')    t = np.arange(len(x_test))    plt.plot(t, y_test, 'r-', linewidth=2, label=u'真实数据')    plt.plot(t, y_hat, 'g-', linewidth=2, label=u'预测数据')    plt.legend(loc='upper right')    plt.title(u'线性回归预测销量', fontsize=18)    plt.grid(b=True)    plt.show()

总结：这里是预测函数主要使用了 LinearRegression()# 使用线性回归模型。这个是sklearn自带的函数.

其中在sklearn自带的函数.几个常用的函数

fit(X,y, [sample_weight])  # 拟合线性模型

-X:训练数据，形状如 [n_samples,n_features]

-y:函数值，形状如 [n_samples, n_targets]

-sample_weight： 每个样本的个体权重,形状如[n_samples]

get_params([deep])  # 获取参数估计量

set_params(**params) # 设置参数估计量

predict(X) # 利用训练好的模型进行预测，返回预测的函数值

-X:预测数据集，形状如 (n_samples, n_features)

score(X, y, [sample_weight]) # 返回预测的决定系数R^2

-X;训练数据，形状如 [n_samples,n_features]

-y;关于X的真实函数值，形状如 (n_samples) or (n_samples, n_outputs)

-sample_weight：样本权重