本文共 4203 字，大约阅读时间需要 14 分钟。

背景： 最近精神上受到打击，时常怀疑人生，怀疑人生的时候，就时常写写算法冷静，今天给小伙伴们介绍图的最小生成树的算法之——Kurskal算法；
…
由于小猿的文采不咋滴，就不长篇大作了，所有故事都在代码里：

package ALG;import java.util.ArrayList;import java.util.HashMap;import java.util.List;import java.util.Scanner;/** * 最小生成树：Kruskal算法； * * 思想： * 1.将边排序，从小到大按边的权寻找两个节点； * 2.如果构成回路，则continue，往下继续寻找; * * */public class Kruskal {    // 用于存储所有边；    private static List<Edge> edges = new ArrayList<>();    // 用来记录当前节点的终结点；    private static HashMap<Character, Character> ed = new HashMap<>();    static Scanner input = new Scanner(System.in);    // 作为内部类，边的属性：权值，起点，终点；    static class Edge {        int weight;        char start;        char end;        Edge(char start, char end, int weight) {            this.start = start;            this.end = end;            this.weight = weight;        }    }    public static void main(String[] args) {        // 初始化，创建一个图；        createGraph();        // 这里利用快排将边按权值从小到大排序（可以用其他排序）；        quickSortGraph(edges);        // 初始化，记录结点当前的状态，初始化设为自己；        for (Edge edge : edges) {            ed.put(edge.start, edge.start);            ed.put(edge.end, edge.end);        }        // 用于存储最小生成树的节点；        List<Edge> result = new ArrayList<>();        // 利用Kruskal算法生成最小生成树；        result = kruskal(edges, ed);        // 记录最小生成树的权值之和；        int minWeight = 0;        for (Edge edge : result) {            minWeight += edge.weight;            System.out.print("( " + edge.start + "," + edge.end + " )\t");        }        System.out.println("the min weight: " + minWeight);    }    private static List<Edge> kruskal(List<Edge> edges, HashMap<Character, Character> ed) {        List<Edge> result = new ArrayList<>();        for (Edge edge : edges) {            // 判断是否会产生回路，判断的方法是：            // 如果start的终点与end的终点是一样的时候，就证明此时会产生回路，返回false；            // 否则，不会产生回路；            if (checkEdgeStatus(edge.start, edge.end, ed)) {                // 不会产生回路的时候，该结点即为最小生成树中的其中一个结点；                result.add(edge);                // 改变所有结点的终点位置；                changeAllEnd(ed, edge.start, edge.end);            }        }        return result;    }    private static void changeAllEnd(HashMap<Character, Character> ed, char start, char end) {        // 用pivot保存start的终点，用于接下来将所有终点为pivot的点更新其终点为end的终点        char pivot = ed.get(start);        for (Character key : ed.keySet()) {            if (ed.get(key) == pivot) {                ed.put(key, ed.get(end));            }        }    }    private static boolean checkEdgeStatus(char start, char end, HashMap<Character, Character> ed) {        // 检查start与end的终点是否相同；        char point1 = ed.get(start);        char point2 = ed.get(end);        return point1 != point2;    }    // 接下来快排的算法（分治，递归）；    private static void quickSortGraph(List<Edge> edges) {        quickSort(edges, 0, edges.size() - 1);    }    private static void quickSort(List<Edge> edges, int start, int end) {        int pivot;        while(start < end) {            pivot = quick(edges, start, end);            quickSort(edges, start, pivot - 1);            start = pivot + 1;        }    }    private static int quick(List<Edge> edges, int start, int end) {        Edge key = edges.get(start);        while(start < end) {            Edge edge;            while (start < end && edges.get(end).weight >= key.weight) {                end --;            }            edge = edges.get(end);            edges.set(start, edge);            while(start < end && edges.get(start).weight <= key.weight) {                start ++;            }            Edge edge1;            edge1 = edges.get(start);            edges.set(end, edge1);        }        edges.set(start, key);        return start;    }    // 创建图；    private static void createGraph() {        while(true) {            char start = input.next().charAt(0);            char end = input.next().charAt(0);            int weight = input.nextInt();            if (weight == -1) {                break;            }            edges.add(new Edge(start, end, weight));        }    }    // 打印所有边的信息    private static void printGraph(List<Edge> edges) {        for (Edge edge : edges) {            System.out.println(edge.start + "-" + edge.end + "-" + edge.weight);        }    }}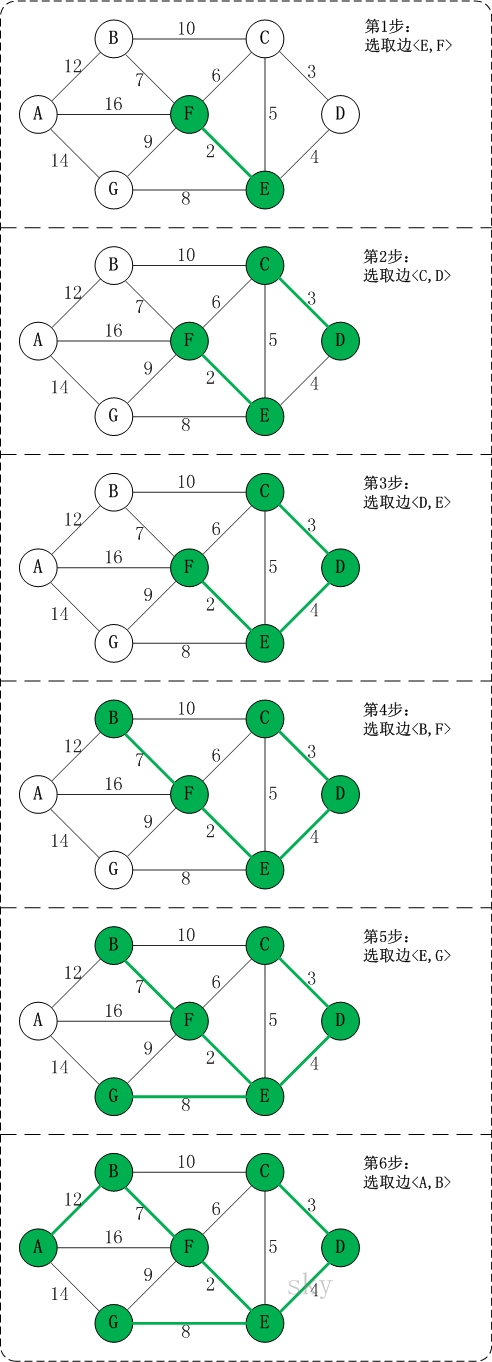

运行结果：

下一篇将介绍最小生成树的另一种算法：Prim 算法