本文共 964 字，大约阅读时间需要 3 分钟。

线性代数之基本向量

什么是线性代数，它有什么特点？概念书籍上有的是，但是它的特点其实就只有两个：

1、可加性：就是说f(x1+x2)=f(x1) + f(x2)

2、比例性：就是说f(kx)=kf(x)

可加性代表了和的函数等于函数的和，这个好理解，就是单纯的加法，比例性代表了比例的函数等于函数的比例，就是说原因和结果的缩放成对应。

说完这个前提，来谈一下向量，这个估计上过高中的都知道，向量和标量，二者的区别在于，向量是有方向性的。向量在物理学上也叫做矢量，矢就是箭的意思。

数学家们的厉害之处在于，它们把几何和代数给搞到一起了，

如果把所有向量的尾部都拉到坐标原点，这样N维 点空间就可以与N维向量建立一一对应的关系。

向量表示的是两点间的位移而不是空间中的物理位置，可是如果向上面所说把向量的尾部固定在坐标原点，就可以用点来表示向量。这是一个给定的前提。

向量的内积（数量积、标积或者点积），几何解释就是一个向量在另外一个向量上的投影的积。

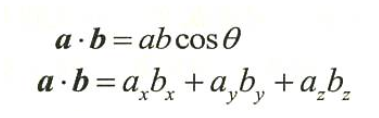
用一个更通俗的例子更容易解释，就是比如你上超市买了几样东西：

价格向量p=(菜1元/斤，米1.5/斤，肉3/斤，酒2元/斤)，数量的向量

d=(2斤，3斤，1斤，6瓶)，那么其内积为：

p*d(1,1.5,3,3)*(2,3,1,6)=1*2 + 1.5*3+3*1+3*6=27.5元。

向量的叉积代表一个垂直于当前两个向量形成的平面的向量。

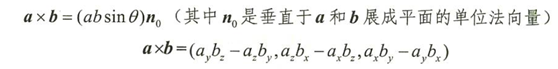
需要注意的是，两个向量的叉积（外积）只能定义于三维空间（三个向量在四维，依次推）。

张量（tensor），网上有一篇“通俗易懂说张量”-Dan Fleisch的视频，是个大老外讲的（真心奇怪，为什么国内的数学或者计算机的大学老师们或者高手们始终不愿意或者说不屑于用普通人或者非专业人士能听懂的话来讲一些基础知识，用某位伟人的话话来说，他们就是不想让人知道）。大家有兴趣可以看看，它总结的最后就是：

张量就是一种表示物理量的方式，这个方式用其向量和分量组合表示物理量，张量所描述的物理量是不随观察者或者说参照系而变化的，当参照系变化时（其实就是基向量变化），其分量也会相应变化，最后结果就是基向量与分量的组合（也就是张量）保持不变。这对于构造数据对象，从而展开分析建模，有着至关重要的意义。

向量的张量积包含了向量的内积和外积的结果。