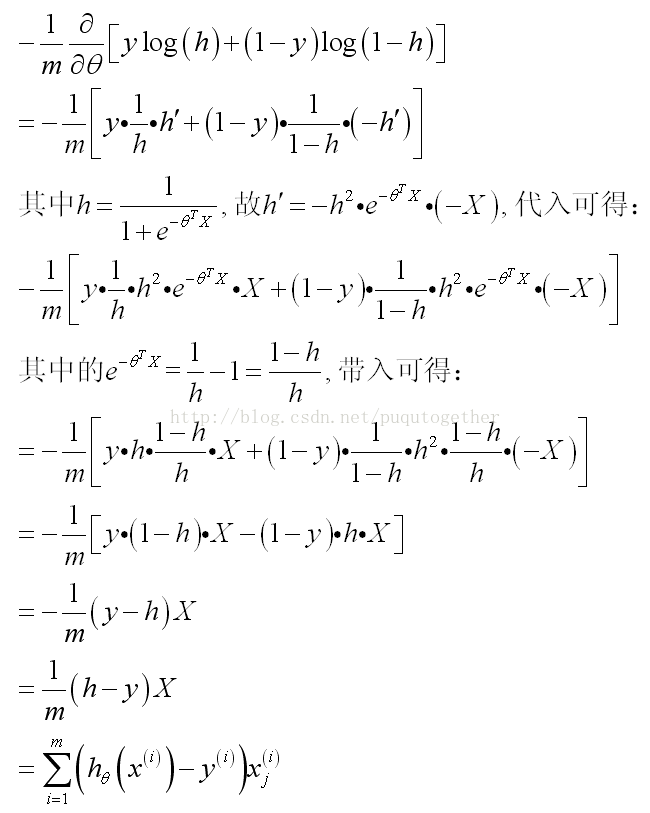本文共 675 字，大约阅读时间需要 2 分钟。

lr：这里指logistic regression; 公式如下：

其他也有：

这里需要非常切记的一点就是该函数的指数部分前面有个负号；我一开始就疑惑为什么会有个符号，如果只看后面这张图的话，看不清道不明，后来想参数也可以调节正负，无关紧要；但看到第一张时，就明白了，一个关系w*x值越大，其logistic映射后其值也会越大；呈正相关；所以必须加负号；因为这里存在一个假设，线性部分计算值越大，其对应正类概率也越大；这种logistic函数也被大家所默认了；该函数输出值就是正类1的概率；

LR的代价函数：

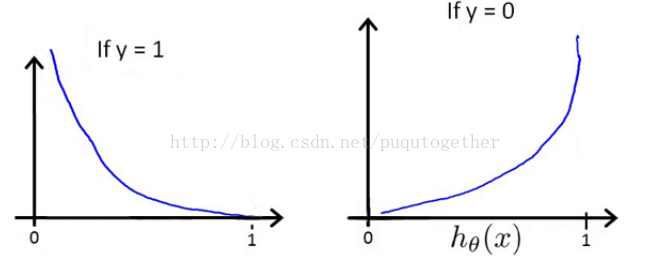
所以，我们需要重新设置代价函数形式。LR中的代价函数如下：

选择这样子的代价函数的原因如下：

• 当实际的y=1和预测的h_theta也为1的时候，误差=0，误差会随着h_theta的变小而增大；当y=0和h_theta=0的时候，误差=0,误差会随着h_theta的增大而增大；
• 代价函数的求导形式和线性模型的求导形式巧妙的相似。（这部分有两个原因，前面已经提到一个了）

2. LR的梯度下降法公式推导

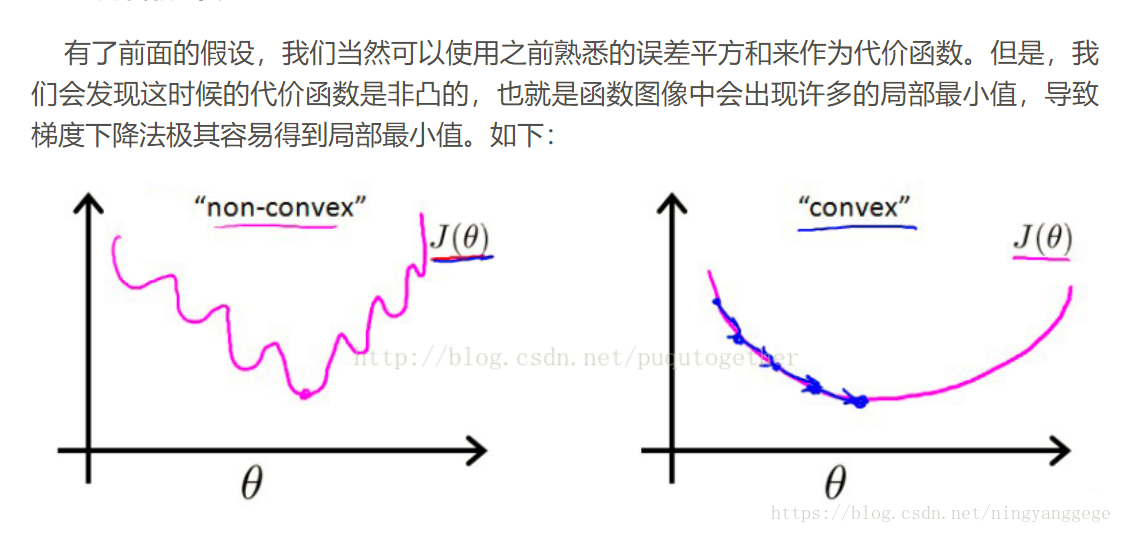
    给定上面定义的假设和代价函数，而且此时的代价函数也是非凸的，我们便可以使用梯度下降法求出令代价函数最小时的theta向量。梯度下降法的基本算法如下：

此时关键的时候要把J_theta对theta的导数求出来。具体的公式推导比较复杂，如下：

（其中的假设我直接用h简单表示）

然后，LR的梯度下降算法就成为了：

这里的j代表某个特征标记；有多少特征就会有多少theta

发现这个形式和前面线性回归模型的梯度下降法巧妙的一致了。

我的推导笔记：