本文共 1379 字，大约阅读时间需要 4 分钟。

摘要：从下面看；

一、傅里叶分析究竟是干什么用的？

在这一章最开始，我想先回答很多人的一个问题：傅里叶分析究竟是干什么用的？这段相对比较枯燥，已经知道了的同学可以直接跳到下一个分割线。

先说一个最直接的用途。无论听广播还是看电视，我们一定对一个词不陌生——频道。频道频道，就是频率的通道，不同的频道就是将不同的频率作为一个通道来进行信息传输。下面大家尝试一件事：先在纸上画一个sin（x），不一定标准，意思差不多就行。不是很难吧。好，接下去画一个sin（3x）+sin（5x）的图形。别说标准不标准了，曲线什么时候上升什么时候下降你都不一定画的对吧？好，画不出来不要紧，我把sin（3x）+sin（5x）的曲线给你，但是前提是你不知道这个曲线的方程式，现在需要你把sin（5x）给我从图里拿出去，看看剩下的是什么。这基本是不可能做到的。但是在频域呢？则简单的很，无非就是几条竖线而已。所以很多在时域看似不可能做到的数学操作，在频域相反很容易。这就是需要傅里叶变换的地方。尤其是从某条曲线中去除一些特定的频率成分，这在工程上称为滤波，是信号处理最重要的概念之一，只有在频域才能轻松的做到。再说一个更重要，但是稍微复杂一点的用途——求解微分方程。（这段有点难度，看不懂的可以直接跳过这段）微分方程的重要性不用我过多介绍了。各行各业都用的到。但是求解微分方程却是一件相当麻烦的事情。因为除了要计算加减乘除，还要计算微分积分。而傅里叶变换则可以让微分和积分在频域中变为乘法和除法，大学数学瞬间变小学算术有没有。

傅里叶分析当然还有其他更重要的用途，我们随着讲随着提；

二、相位谱：

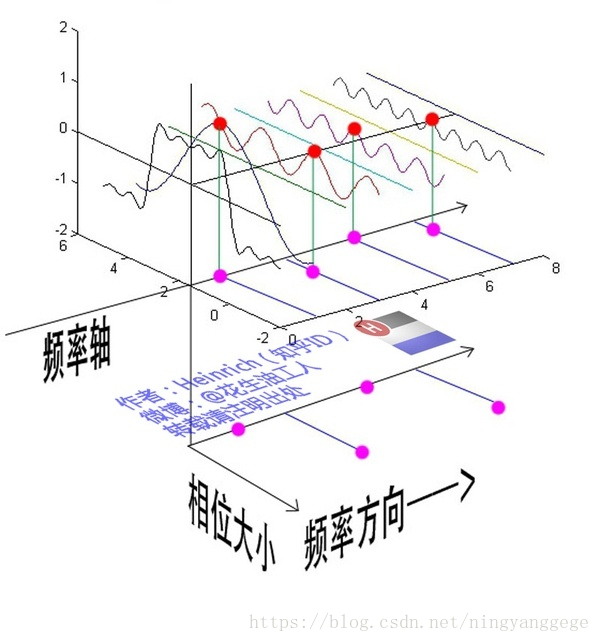
一个完整正弦波公式：A.sin(wt+θ)；A代表振幅，w代表频率，θ代表相位；不同相位决定了波的位置，所以对于频域分析，仅仅有频谱（振幅谱）是不够的，我们还需要一个相位谱。那么这个相位谱在哪呢？我们看下图，这次为了避免图片太混论，我们用7个波叠加的图

鉴于正弦波是周期的，我们需要设定一个用来标记正弦波位置的东西。在图中就是那些小红点。小红点是距离频率轴最近的波峰，而这个波峰所处的位置离频率轴有多远呢？为了看的更清楚，我们将红色的点投影到下平面，投影点我们用粉色点来表示。当然，这些粉色的点只标注了波峰距离频率轴的距离，并不是相位

这里需要纠正一个概念：时间差并不是相位差。如果将全部周期看作2Pi或者360度的话，相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘2Pi，就得到了相位差。 在完整的立体图中，我们将投影得到的时间差依次除以所在频率的周期，就得到了最下面的相位谱。所以，频谱是从侧面看，相位谱是从下面看。下次偷看女生裙底被发现的话，可以告诉她：“对不起，我只是想看看你的相位谱。” 注意到，相位谱中的相位除了0，就是Pi。因为cos（t+Pi）=-cos（t），所以实际上相位为Pi的波只是上下翻转了而已。对于周期方波的傅里叶级数，这样的相位谱已经是很简单的了。另外值得注意的是，由于cos（t+2Pi）=cos（t），所以相位差是周期的，pi和3pi，5pi，7pi都是相同的相位。人为定义相位谱的值域为(-pi，pi]，所以图中的相位差均为Pi。 最后来一张大集合：

参考：http://blog.jobbole.com/70549/